
|
Probability density function  | |||
|
Cumulative distribution function 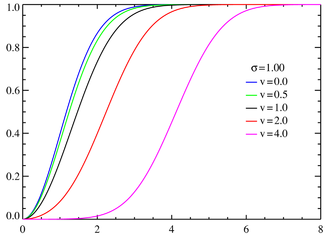 | |||
| Parameters |
, distance between the reference point and the center of the bivariate distribution, , scale | ||
|---|---|---|---|
| Support | |||
| CDF |
where Q1 is the Marcum Q-function | ||
| Mean | |||
| Variance | |||
| Skewness | (complicated) | ||
| Ex. kurtosis | (complicated) | ||
In probability theory, the Rice distribution or Rician distribution (or, less commonly, Ricean distribution) is the probability distribution of the magnitude of a circularly-symmetric bivariate normal random variable, possibly with non-zero mean (noncentral). It was named after Stephen O. Rice (1907–1986).
YouTube Encyclopedic
-
1/5Views:7 9783 86718 5055 7792 598
-
Fortified Rice Distribution In Government Schemes: Latest update | Drishti IAS English
-
Rice | production and distribution in india | important locations | cultural importance its problems
-
RICE origin, Distribution, Economics, Climate & Soil• Go For Agriculture Education #icar #bhu #ibps
-
Distribution Of Rice 🍚 In India | Part-4 Of Cultivation Of Rice In India | Completes Notes
-
Rice distribution
Transcription
Characterization
The probability density function is
where I0(z) is the modified Bessel function of the first kind with order zero.
In the context of Rician fading, the distribution is often also rewritten using the Shape Parameter , defined as the ratio of the power contributions by line-of-sight path to the remaining multipaths, and the Scale parameter , defined as the total power received in all paths.[1]
The characteristic function of the Rice distribution is given as:[2][3]
where is one of Horn's confluent hypergeometric functions with two variables and convergent for all finite values of and . It is given by:[4][5]
where
is the rising factorial.
Properties
Moments
The first few raw moments are:
and, in general, the raw moments are given by
Here Lq(x) denotes a Laguerre polynomial:
where is the confluent hypergeometric function of the first kind. When k is even, the raw moments become simple polynomials in σ and ν, as in the examples above.
For the case q = 1/2:
The second central moment, the variance, is
Note that indicates the square of the Laguerre polynomial , not the generalized Laguerre polynomial
Related distributions
- if where and are statistically independent normal random variables and is any real number.
- Another case where comes from the following steps:
- Generate having a Poisson distribution with parameter (also mean, for a Poisson)
- Generate having a chi-squared distribution with 2P + 2 degrees of freedom.
- Set
- If then has a noncentral chi-squared distribution with two degrees of freedom and noncentrality parameter .
- If then has a noncentral chi distribution with two degrees of freedom and noncentrality parameter .
- If then , i.e., for the special case of the Rice distribution given by , the distribution becomes the Rayleigh distribution, for which the variance is .
- If then has an exponential distribution.[6]
- If then has an Inverse Rician distribution.[7]
- The folded normal distribution is the univariate special case of the Rice distribution.
Limiting cases
For large values of the argument, the Laguerre polynomial becomes[8]
It is seen that as ν becomes large or σ becomes small the mean becomes ν and the variance becomes σ2.
The transition to a Gaussian approximation proceeds as follows. From Bessel function theory we have
so, in the large region, an asymptotic expansion of the Rician distribution:
Moreover, when the density is concentrated around and because of the Gaussian exponent, we can also write and finally get the Normal approximation
The approximation becomes usable for
Parameter estimation (the Koay inversion technique)
There are three different methods for estimating the parameters of the Rice distribution, (1) method of moments,[9][10][11][12] (2) method of maximum likelihood,[9][10][11][13] and (3) method of least squares.[citation needed] In the first two methods the interest is in estimating the parameters of the distribution, ν and σ, from a sample of data. This can be done using the method of moments, e.g., the sample mean and the sample standard deviation. The sample mean is an estimate of μ1' and the sample standard deviation is an estimate of μ21/2.
The following is an efficient method, known as the "Koay inversion technique".[14] for solving the estimating equations, based on the sample mean and the sample standard deviation, simultaneously . This inversion technique is also known as the fixed point formula of SNR. Earlier works[9][15] on the method of moments usually use a root-finding method to solve the problem, which is not efficient.
First, the ratio of the sample mean to the sample standard deviation is defined as r, i.e., . The fixed point formula of SNR is expressed as
where is the ratio of the parameters, i.e., , and is given by:
where and are modified Bessel functions of the first kind.
Note that is a scaling factor of and is related to by:
To find the fixed point, , of , an initial solution is selected, , that is greater than the lower bound, which is and occurs when [14] (Notice that this is the of a Rayleigh distribution). This provides a starting point for the iteration, which uses functional composition,[clarification needed] and this continues until is less than some small positive value. Here, denotes the composition of the same function, , times. In practice, we associate the final for some integer as the fixed point, , i.e., .
Once the fixed point is found, the estimates and are found through the scaling function, , as follows:
and
To speed up the iteration even more, one can use the Newton's method of root-finding.[14] This particular approach is highly efficient.
Applications
- The Euclidean norm of a bivariate circularly-symmetric normally distributed random vector.
- Rician fading (for multipath interference))
- Effect of sighting error on target shooting.[16]
- Analysis of diversity receivers in radio communications.[17][18]
- Distribution of eccentricities for models of the inner Solar System after long-term numerical integration.[19]
See also
References
- ^ Abdi, A. and Tepedelenlioglu, C. and Kaveh, M. and Giannakis, G., "On the estimation of the K parameter for the Rice fading distribution", IEEE Communications Letters, March 2001, p. 92–94
- ^ Liu 2007 (in one of Horn's confluent hypergeometric functions with two variables).
- ^ Annamalai 2000 (in a sum of infinite series).
- ^ Erdelyi 1953.
- ^ Srivastava 1985.
- ^ Richards, M.A., Rice Distribution for RCS, Georgia Institute of Technology (Sep 2006)
- ^ Jones, Jessica L., Joyce McLaughlin, and Daniel Renzi. "The noise distribution in a shear wave speed image computed using arrival times at fixed spatial positions.", Inverse Problems 33.5 (2017): 055012.
- ^ Abramowitz and Stegun (1968) §13.5.1
- ^ a b c Talukdar et al. 1991
- ^ a b Bonny et al. 1996
- ^ a b Sijbers et al. 1998
- ^ den Dekker and Sijbers 2014
- ^ Varadarajan and Haldar 2015
- ^ a b c Koay et al. 2006 (known as the SNR fixed point formula).
- ^ Abdi 2001
- ^ "Ballistipedia". Retrieved 4 May 2014.
- ^ Beaulieu, Norman C; Hemachandra, Kasun (September 2011). "Novel Representations for the Bivariate Rician Distribution". IEEE Transactions on Communications. 59 (11): 2951–2954. doi:10.1109/TCOMM.2011.092011.090171. S2CID 1221747.
- ^ Dharmawansa, Prathapasinghe; Rajatheva, Nandana; Tellambura, Chinthananda (March 2009). "New Series Representation for the Trivariate Non-Central Chi-Squared Distribution" (PDF). IEEE Transactions on Communications. 57 (3): 665–675. CiteSeerX 10.1.1.582.533. doi:10.1109/TCOMM.2009.03.070083. S2CID 15706035.
- ^ Laskar, J. (1 July 2008). "Chaotic diffusion in the Solar System". Icarus. 196 (1): 1–15. arXiv:0802.3371. Bibcode:2008Icar..196....1L. doi:10.1016/j.icarus.2008.02.017. ISSN 0019-1035. S2CID 11586168.
Further reading
- Abramowitz, M. and Stegun, I. A. (ed.), Handbook of Mathematical Functions, National Bureau of Standards, 1964; reprinted Dover Publications, 1965. ISBN 0-486-61272-4
- Rice, S. O., Mathematical Analysis of Random Noise. Bell System Technical Journal 24 (1945) 46–156.
- I. Soltani Bozchalooi; Ming Liang (20 November 2007). "A smoothness index-guided approach to wavelet parameter selection in signal de-noising and fault detection". Journal of Sound and Vibration. 308 (1–2): 253–254. Bibcode:2007JSV...308..246B. doi:10.1016/j.jsv.2007.07.038.
- Wang, Dong; Zhou, Qiang; Tsui, Kwok-Leung (2017). "On the distribution of the modulus of Gabor wavelet coefficients and the upper bound of the dimensionless smoothness index in the case of additive Gaussian noises: Revisited". Journal of Sound and Vibration. 395: 393–400. doi:10.1016/j.jsv.2017.02.013.
- Liu, X. and Hanzo, L., A Unified Exact BER Performance Analysis of Asynchronous DS-CDMA Systems Using BPSK Modulation over Fading Channels, IEEE Transactions on Wireless Communications, Volume 6, Issue 10, October 2007, pp. 3504–3509.
- Annamalai, A., Tellambura, C. and Bhargava, V. K., Equal-Gain Diversity Receiver Performance in Wireless Channels, IEEE Transactions on Communications, Volume 48, October 2000, pp. 1732–1745.
- Erdelyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G., Higher Transcendental Functions, Volume 1. Archived 11 August 2011 at the Wayback Machine McGraw-Hill Book Company Inc., 1953.
- Srivastava, H. M. and Karlsson, P. W., Multiple Gaussian Hypergeometric Series. Ellis Horwood Ltd., 1985.
- Sijbers J., den Dekker A. J., Scheunders P. and Van Dyck D., "Maximum Likelihood estimation of Rician distribution parameters" Archived 19 October 2011 at the Wayback Machine, IEEE Transactions on Medical Imaging, Vol. 17, Nr. 3, pp. 357–361, (1998)
- Varadarajan D. and Haldar J. P., "A Majorize-Minimize Framework for Rician and Non-Central Chi MR Images", IEEE Transactions on Medical Imaging, Vol. 34, no. 10, pp. 2191–2202, (2015)
- den Dekker, A.J.; Sijbers, J (December 2014). "Data distributions in magnetic resonance images: a review". Physica Medica. 30 (7): 725–741. doi:10.1016/j.ejmp.2014.05.002. PMID 25059432.
- Koay, C.G. and Basser, P. J., Analytically exact correction scheme for signal extraction from noisy magnitude MR signals, Journal of Magnetic Resonance, Volume 179, Issue = 2, p. 317–322, (2006)
- Abdi, A., Tepedelenlioglu, C., Kaveh, M., and Giannakis, G. On the estimation of the K parameter for the Rice fading distribution, IEEE Communications Letters, Volume 5, Number 3, March 2001, pp. 92–94.
- Talukdar, K.K.; Lawing, William D. (March 1991). "Estimation of the parameters of the Rice distribution". Journal of the Acoustical Society of America. 89 (3): 1193–1197. Bibcode:1991ASAJ...89.1193T. doi:10.1121/1.400532.
- Bonny, J.M.; Renou, J.P.; Zanca, M. (November 1996). "Optimal Measurement of Magnitude and Phase from MR Data". Journal of Magnetic Resonance, Series B. 113 (2): 136–144. Bibcode:1996JMRB..113..136B. doi:10.1006/jmrb.1996.0166. PMID 8954899.
External links
- MATLAB code for Rice/Rician distribution (PDF, mean and variance, and generating random samples)











![{\displaystyle {\begin{aligned}\chi _{X}(t\mid \nu ,\sigma )=\exp \left(-{\frac {\nu ^{2}}{2\sigma ^{2}}}\right)&\left[\Psi _{2}\left(1;1,{\frac {1}{2}};{\frac {\nu ^{2}}{2\sigma ^{2}}},-{\frac {1}{2}}\sigma ^{2}t^{2}\right)\right.\\[8pt]&\left.{}+i{\sqrt {2}}\sigma t\Psi _{2}\left({\frac {3}{2}};1,{\frac {3}{2}};{\frac {\nu ^{2}}{2\sigma ^{2}}},-{\frac {1}{2}}\sigma ^{2}t^{2}\right)\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78e23ca2a48dd2b11c2e5ca46a8f017950308c55)









![{\displaystyle {\begin{aligned}L_{1/2}(x)&=\,_{1}F_{1}\left(-{\frac {1}{2}};1;x\right)\\&=e^{x/2}\left[\left(1-x\right)I_{0}\left(-{\frac {x}{2}}\right)-xI_{1}\left(-{\frac {x}{2}}\right)\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7baebb5240ced1a2464e31b42c0a0513eb18f296)



































![g(\theta )={\sqrt {\xi {(\theta )}\left[1+r^{2}\right]-2}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/3475731daba192c855cd90f039f3a56a2bc26321)


![\xi {\left(\theta \right)}=2+\theta ^{2}-{\frac {\pi }{8}}\exp {(-\theta ^{2}/2)}\left[(2+\theta ^{2})I_{0}(\theta ^{2}/4)+\theta ^{2}I_{1}(\theta ^{{2}}/4)\right]^{2},](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c016f1732f8a5a3bc72b406e9c40d7023f1f621)

















