


In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q are not coprime (in which case the number of components is gcd(p, q)). A torus knot is trivial (equivalent to the unknot) if and only if either p or q is equal to 1 or −1. The simplest nontrivial example is the (2,3)-torus knot, also known as the trefoil knot.

YouTube Encyclopedic
-
1/4Views:7 6436785364 516
-
Torus knots
-
The torus knot (4,3)
-
Torus knot animation
-
3d Studio Max 132 - Creating Torus Knot
Transcription
Geometrical representation
A torus knot can be rendered geometrically in multiple ways which are topologically equivalent (see Properties below) but geometrically distinct. The convention used in this article and its figures is the following.
The (p,q)-torus knot winds q times around a circle in the interior of the torus, and p times around its axis of rotational symmetry.[note 1]. If p and q are not relatively prime, then we have a torus link with more than one component.
The direction in which the strands of the knot wrap around the torus is also subject to differing conventions. The most common is to have the strands form a right-handed screw for p q > 0.[3][4][5]
The (p,q)-torus knot can be given by the parametrization
where and . This lies on the surface of the torus given by (in cylindrical coordinates).
Other parameterizations are also possible, because knots are defined up to continuous deformation. The illustrations for the (2,3)- and (3,8)-torus knots can be obtained by taking , and in the case of the (2,3)-torus knot by furthermore subtracting respectively and from the above parameterizations of x and y. The latter generalizes smoothly to any coprime p,q satisfying .
Properties

A torus knot is trivial iff either p or q is equal to 1 or −1.[4][5]
Each nontrivial torus knot is prime[6] and chiral.[4]
The (p,q) torus knot is equivalent to the (q,p) torus knot.[3][5] This can be proved by moving the strands on the surface of the torus.[7] The (p,−q) torus knot is the obverse (mirror image) of the (p,q) torus knot.[5] The (−p,−q) torus knot is equivalent to the (p,q) torus knot except for the reversed orientation.

Any (p,q)-torus knot can be made from a closed braid with p strands. The appropriate braid word is [8]
(This formula assumes the common convention that braid generators are right twists,[4][8][9][10] which is not followed by the Wikipedia page on braids.)
The crossing number of a (p,q) torus knot with p,q > 0 is given by
- c = min((p−1)q, (q−1)p).
The genus of a torus knot with p,q > 0 is
The Alexander polynomial of a torus knot is [3][8]
- where
The Jones polynomial of a (right-handed) torus knot is given by
The complement of a torus knot in the 3-sphere is a Seifert-fibered manifold, fibred over the disc with two singular fibres.
Let Y be the p-fold dunce cap with a disk removed from the interior, Z be the q-fold dunce cap with a disk removed from its interior, and X be the quotient space obtained by identifying Y and Z along their boundary circle. The knot complement of the (p, q) -torus knot deformation retracts to the space X. Therefore, the knot group of a torus knot has the presentation
Torus knots are the only knots whose knot groups have nontrivial center (which is infinite cyclic, generated by the element in the presentation above).
The stretch factor of the (p,q) torus knot, as a curve in Euclidean space, is Ω(min(p,q)), so torus knots have unbounded stretch factors. Undergraduate researcher John Pardon won the 2012 Morgan Prize for his research proving this result, which solved a problem originally posed by Mikhail Gromov.[11][12]
Connection to complex hypersurfaces
The (p,q)−torus knots arise when considering the link of an isolated complex hypersurface singularity. One intersects the complex hypersurface with a hypersphere, centred at the isolated singular point, and with sufficiently small radius so that it does not enclose, nor encounter, any other singular points. The intersection gives a submanifold of the hypersphere.
Let p and q be coprime integers, greater than or equal to two. Consider the holomorphic function given by Let be the set of such that Given a real number we define the real three-sphere as given by The function has an isolated critical point at since if and only if Thus, we consider the structure of close to In order to do this, we consider the intersection This intersection is the so-called link of the singularity The link of , where p and q are coprime, and both greater than or equal to two, is exactly the (p,q)−torus knot.[13]
List

The figure on the right is torus link (72,4) .
- Unknot, 31 knot (3,2), 51 knot (5,2), 71 knot (7,2), 819 knot (4,3), 91 knot (9,2), 10124 knot (5,3)
| Table # |
A-B | Image | P | Q | Cross # |
|---|---|---|---|---|---|
| 0 | 01 | 
|
0 | ||
| 3a1 | 31 | 
|
2 | 3 | 3 |
| 5a2 | 51 | 
|
2 | 5 | 5 |
| 7a7 | 71 | 
|
2 | 7 | 7 |
| 8n3 | 819 | 
|
3 | 4 | 8 |
| 9a41 | 91 | 
|
2 | 9 | 9 |
| 10n21 | 10124 | 
|
3 | 5 | 10 |
| 11a367 | 
|
2 | 11 | 11 | |
| 13a4878 | 
|
2 | 13 | 13 | |
| 14n21881 | 
|
3 | 7 | 14 | |
| 15n41185 | 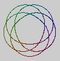
|
4 | 5 | 15 | |
| 15a85263 | 2 | 15 | 15 | ||
| 16n783154 | 
|
3 | 8 | 16 | |
| 2 | 17 | 17 | |||
| 2 | 19 | 19 | |||
| 3 | 10 | 20 | |||

|
4 | 7 | 21 | ||
| 2 | 21 | 21 | |||
| 3 | 11 | 22 | |||
| 2 | 23 | 23 | |||

|
5 | 6 | 24 | ||
| 2 | 25 | 25 | |||
| 3 | 13 | 26 | |||

|
4 | 9 | 27 | ||
| 2 | 27 | 27 | |||

|
5 | 7 | 28 | ||
| 3 | 14 | 28 | |||
| 2 | 29 | 29 | |||
| 2 | 31 | 31 | |||

|
5 | 8 | 32 | ||
| 3 | 16 | 32 | |||
| 4 | 11 | 33 | |||
| 2 | 33 | 33 | |||
| 3 | 17 | 34 | |||

|
6 | 7 | 35 | ||
| 2 | 35 | 35 | |||

|
5 | 9 | 36 | ||
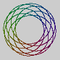
|
7 | 8 | 48 | ||

|
7 | 9 | 54 | ||

|
8 | 9 | 63 |
g-torus knot
A g-torus knot is a closed curve drawn on a g-torus. More technically, it is the homeomorphic image of a circle in S³ which can be realized as a subset of a genus g handlebody in S³ (whose complement is also a genus g handlebody). If a link is a subset of a genus two handlebody, it is a double torus link.[14]
For genus two, the simplest example of a double torus knot that is not a torus knot is the figure-eight knot.[15][16]
Notes
See also
References
- ^ Torus Knot on Wolfram Mathworld [1].
- ^ "36 Torus Knots", The Knot Atlas. [2].
- ^ a b c Livingston, Charles (1993). Knot Theory. Mathematical Association of America. p. [page needed]. ISBN 0-88385-027-3.
- ^ a b c d Murasugi, Kunio (1996). Knot Theory and its Applications. Birkhäuser. p. [page needed]. ISBN 3-7643-3817-2.
- ^ a b c d Kawauchi, Akio (1996). A Survey of Knot Theory. Birkhäuser. p. [page needed]. ISBN 3-7643-5124-1.
- ^ Norwood, F. H. (1982-01-01). "Every two-generator knot is prime". Proceedings of the American Mathematical Society. 86 (1): 143–147. doi:10.1090/S0002-9939-1982-0663884-7. ISSN 0002-9939. JSTOR 2044414.
- ^ Baker, Kenneth (2011-03-28). "p q is q p". Sketches of Topology. Retrieved 2020-11-09.
- ^ a b c Lickorish, W. B. R. (1997). An Introduction to Knot Theory. Springer. p. [page needed]. ISBN 0-387-98254-X.
- ^ Dehornoy, P.; Dynnikov, Ivan; Rolfsen, Dale; Wiest, Bert (2000). Why are Braids Orderable? (PDF). p. [page needed]. Archived from the original (PDF) on 2012-04-15. Retrieved 2011-11-12.
- ^ Birman, J. S.; Brendle, T. E. (2005). "Braids: a Survey". In Menasco, W.; Thistlethwaite, M. (eds.). Handbook of Knot Theory. Elsevier. p. [page needed]. ISBN 0-444-51452-X.
- ^ Kehoe, Elaine (April 2012), "2012 Morgan Prize", Notices of the American Mathematical Society, vol. 59, no. 4, pp. 569–571, doi:10.1090/noti825.
- ^ Pardon, John (2011), "On the distortion of knots on embedded surfaces", Annals of Mathematics, Second Series, 174 (1): 637–646, arXiv:1010.1972, doi:10.4007/annals.2011.174.1.21, MR 2811613, S2CID 55567836
- ^ Milnor, J. (1968). Singular Points of Complex Hypersurfaces. Princeton University Press. p. [page needed]. ISBN 0-691-08065-8.
- ^ Rolfsen, Dale (1976). Knots and Links. Publish or Perish, Inc. p. [page needed]. ISBN 0-914098-16-0.
- ^ Hill, Peter (December 1999). "On Double-Torus Knots (I)". Journal of Knot Theory and Its Ramifications. 08 (8): 1009–1048. doi:10.1142/S0218216599000651. ISSN 0218-2165.
- ^ Norwood, Frederick (November 1989). "Curves on surfaces". Topology and Its Applications. 33 (3): 241–246. doi:10.1016/0166-8641(89)90105-3.
External links
- "36 Torus Knots", The Knot Atlas.
- Weisstein, Eric W. "Torus Knot". MathWorld.
- Torus knot renderer in Actionscript
- Fun with the PQ-Torus Knot
































