Satellite knot

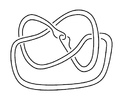
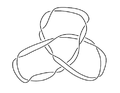
In the mathematical theory of knots, a satellite knot is a knot that contains an incompressible, non boundary-parallel torus in its complement.^[1] Every knot is either hyperbolic, a torus, or a satellite knot. The class of satellite knots include composite knots, cable knots, and Whitehead doubles. A satellite link is one that orbits a companion knot K in the sense that it lies inside a regular neighborhood of the companion.^[2]: 217

A satellite knot ${\displaystyle K}$ can be picturesquely described as follows: start by taking a nontrivial knot ${\displaystyle K'}$ lying inside an unknotted solid torus ${\displaystyle V}$. Here "nontrivial" means that the knot ${\displaystyle K'}$ is not allowed to sit inside of a 3-ball in ${\displaystyle V}$ and ${\displaystyle K'}$ is not allowed to be isotopic to the central core curve of the solid torus. Then tie up the solid torus into a nontrivial knot.

This means there is a non-trivial embedding ${\displaystyle f\colon V\to S^{3}}$ and ${\displaystyle K=f\left(K'\right)}$. The central core curve of the solid torus ${\displaystyle V}$ is sent to a knot ${\displaystyle H}$, which is called the "companion knot" and is thought of as the planet around which the "satellite knot" ${\displaystyle K}$ orbits. The construction ensures that ${\displaystyle f(\partial V)}$ is a non-boundary parallel incompressible torus in the complement of ${\displaystyle K}$. Composite knots contain a certain kind of incompressible torus called a swallow-follow torus, which can be visualized as swallowing one summand and following another summand.

Since ${\displaystyle V}$ is an unknotted solid torus, ${\displaystyle S^{3}\setminus V}$ is a tubular neighbourhood of an unknot ${\displaystyle J}$. The 2-component link ${\displaystyle K'\cup J}$ together with the embedding ${\displaystyle f}$ is called the pattern associated to the satellite operation.

A convention: people usually demand that the embedding ${\displaystyle f\colon V\to S^{3}}$ is untwisted in the sense that ${\displaystyle f}$ must send the standard longitude of ${\displaystyle V}$ to the standard longitude of ${\displaystyle f(V)}$. Said another way, given any two disjoint curves ${\displaystyle c_{1},c_{2}\subset V}$, ${\displaystyle f}$ preserves their linking numbers i.e.: ${\displaystyle \operatorname {lk} (f(c_{1}),f(c_{2}))=\operatorname {lk} (c_{1},c_{2})}$.

Basic families

When ${\displaystyle K'\subset \partial V}$ is a torus knot, then ${\displaystyle K}$ is called a cable knot. Examples 3 and 4 are cable knots. The cable constructed with given winding numbers (m,n) from another knot K, is often called the (m,n) cable of K.

If ${\displaystyle K'}$ is a non-trivial knot in ${\displaystyle S^{3}}$ and if a compressing disc for ${\displaystyle V}$ intersects ${\displaystyle K'}$ in precisely one point, then ${\displaystyle K}$ is called a connect-sum. Another way to say this is that the pattern ${\displaystyle K'\cup J}$ is the connect-sum of a non-trivial knot ${\displaystyle K'}$ with a Hopf link.

If the link ${\displaystyle K'\cup J}$ is the Whitehead link, ${\displaystyle K}$ is called a Whitehead double. If ${\displaystyle f}$ is untwisted, ${\displaystyle K}$ is called an untwisted Whitehead double.

Examples

• 

  Example 1: A connect-sum of a trefoil and figure-8 knot.

• 

  Example 2: The Whitehead double of the figure-8.

• 

  Example 3: A cable of a connect-sum.

• 

  Example 4: A cable of a trefoil.

• 

  Example 5: A knot which is a 2-fold satellite i.e.: it has non-parallel swallow-follow tori.

• 

  Example 6: A knot which is a 2-fold satellite i.e.: it has non-parallel swallow-follow tori.

Examples 5 and 6 are variants on the same construction. They both have two non-parallel, non-boundary-parallel incompressible tori in their complements, splitting the complement into the union of three manifolds. In 5, those manifolds are: the Borromean rings complement, trefoil complement, and figure-8 complement. In 6, the figure-8 complement is replaced by another trefoil complement.

Origins

In 1949 ^[3] Horst Schubert proved that every oriented knot in ${\displaystyle S^{3}}$ decomposes as a connect-sum of prime knots in a unique way, up to reordering, making the monoid of oriented isotopy-classes of knots in ${\displaystyle S^{3}}$ a free commutative monoid on countably-infinite many generators. Shortly after, he realized he could give a new proof of his theorem by a close analysis of the incompressible tori present in the complement of a connect-sum. This led him to study general incompressible tori in knot complements in his epic work Knoten und Vollringe,^[4] where he defined satellite and companion knots.

Follow-up work

Schubert's demonstration that incompressible tori play a major role in knot theory was one several early insights leading to the unification of 3-manifold theory and knot theory. It attracted Waldhausen's attention, who later used incompressible surfaces to show that a large class of 3-manifolds are homeomorphic if and only if their fundamental groups are isomorphic.^[5] Waldhausen conjectured what is now the Jaco–Shalen–Johannson-decomposition of 3-manifolds, which is a decomposition of 3-manifolds along spheres and incompressible tori. This later became a major ingredient in the development of geometrization, which can be seen as a partial-classification of 3-dimensional manifolds. The ramifications for knot theory were first described in the long-unpublished manuscript of Bonahon and Siebenmann.^[6]

Uniqueness of satellite decomposition

In Knoten und Vollringe, Schubert proved that in some cases, there is essentially a unique way to express a knot as a satellite. But there are also many known examples where the decomposition is not unique.^[7] With a suitably enhanced notion of satellite operation called splicing, the JSJ decomposition gives a proper uniqueness theorem for satellite knots.^[8][9]

See also

• Hyperbolic knot
• Torus knot

References

This page was last edited on 7 August 2023, at 18:52