List of mathematical knots and links

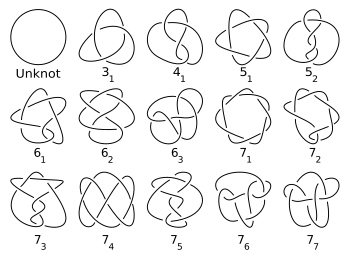
This article contains a list of mathematical knots and links. See also list of knots, list of geometric topology topics.

Knots

Prime knots

• 0₁ knot/Unknot - a simple un-knotted closed loop
• 3₁ knot/Trefoil knot - (2,3)-torus knot, the two loose ends of a common overhand knot joined together
• 4₁ knot/Figure-eight knot (mathematics) - a prime knot with a crossing number four
• 5₁ knot/Cinquefoil knot, (5,2)-torus knot, Solomon's seal knot, pentafoil knot - a prime knot with crossing number five which can be arranged as a {5/2} star polygon (pentagram)
• 5₂ knot/Three-twist knot - the twist knot with three-half twists
• 6₁ knot/Stevedore knot (mathematics) - a prime knot with crossing number six, it can also be described as a twist knot with four twists
• 6₂ knot - a prime knot with crossing number six
• 6₃ knot - a prime knot with crossing number six
• 7₁ knot, septafoil knot, (7,2)-torus knot - a prime knot with crossing number seven, which can be arranged as a {7/2} star polygon (heptagram)
• 7₄ knot, "endless knot"
• 8₁₈ knot, "carrick mat"
• 10₁₆₁/10₁₆₂, known as the Perko pair; this was a single knot listed twice in Dale Rolfsen's knot table; the duplication was discovered by Kenneth Perko
• 12n242/(−2,3,7) pretzel knot
• (p, q)-torus knot - a special kind of knot that lies on the surface of an unknotted torus in R³

Composite

• Square knot (mathematics) - a composite knot obtained by taking the connected sum of a trefoil knot with its reflection
• Granny knot (mathematics) - a composite knot obtained by taking the connected sum of two identical trefoil knots

Links

• 0²
  ₁ link/Unlink - equivalent under ambient isotopy to finitely many disjoint circles in the plane
• 2²
  ₁ link/Hopf link - the simplest nontrivial link with more than one component; it consists of two circles linked together exactly once (L2a1)
• 4²
  ₁ link/Solomon's knot (a two component "link" rather than a one component "knot") - a traditional decorative motif used since ancient times (L4a1)
• 5²
  ₁ link/Whitehead link - two projections of the unknot: one circular loop and one figure eight-shaped loop intertwined such that they are inseparable and neither loses its form (L5a1)
• Brunnian link - a nontrivial link that becomes trivial if any component is removed
• 6³
  ₂ link/Borromean rings - three topological circles which are linked and form a Brunnian link (L6a4)
• L10a140 link - presumably the simplest non-Borromean Brunnian link
• Pretzel link - a Montesinos link with integer tangles

External links

• "Catalogue of all knots and links with 11 or fewer crossings (wiki)", The Knot Atlas.

This page was last edited on 12 September 2023, at 23:35