L10a140 link

L10a140
Braid length	10
Braid no.	3
Crossing no.	10
Hyperbolic volume	12.27627758
Conway notation	[.3:30]
Thistlethwaite	L10a140
Other
alternating

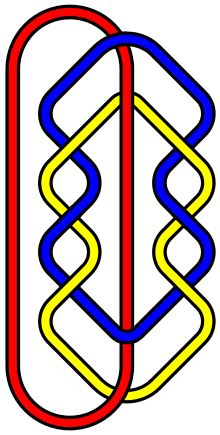
In the mathematical theory of knots, L10a140 is the name in the Thistlethwaite link table of a link of three loops, which has ten crossings between the loops when presented in its simplest visual form.^[1] It is of interest because it is presumably the simplest link which possesses the Brunnian property — a link of connected components that, when one component is removed, becomes entirely unconnected^[2] — other than the six-crossing Borromean rings.^[3]

In other words, no two loops are directly linked with each other, but all three are collectively interlinked, so removing any loop frees the other two. In the image in the infobox at right, the red loop is not interlinked with either the blue or the yellow loops, and if the red loop is removed, then the blue and yellow loops can also be disentangled from each other without cutting either one.

According to work by Slavik V. Jablan, the L10a140 link can be seen as the second in an infinite series of Brunnian links beginning with the Borromean rings. So if the blue and yellow loops have only one twist along each side, the resulting configuration is the Borromean rings; if the blue and yellow loops have three twists along each side, the resulting configuration is the L10a140 link; if the blue and yellow loops have five twists along each side, the resulting configuration is a three-loop link with 14 overall crossings, etc. etc.^[4]

Invariants

The multivariable Alexander polynomial for the L10a140 link is

${\displaystyle \Delta (u,v,w)={\frac {(u-1)(v-1)(w-1)(vw+1)^{2}}{vw{\sqrt {uvw}}}},\,}$

the Conway polynomial is

${\displaystyle \nabla (z)=4z^{4}+4z^{6}+z^{8},\,}$

the Jones polynomial factors nicely as

${\displaystyle {\begin{aligned}V(t)&=-t^{5}+3t^{4}-5t^{3}+8t^{2}-9t+12-9t^{-1}+8t^{-2}-5t^{-3}+3t^{-4}-t^{-5}\\[8pt]&=-{\frac {1}{t^{5}}}\left(t^{5}-2t^{4}+t^{3}-2t^{2}+t-1\right)\left(t^{5}-t^{4}+2t^{3}-t^{2}+2t-1\right)\\[8pt]&=w(t)w(1/t),\,\end{aligned}}}$

where ${\displaystyle w(t)=t^{5}-2t^{4}+t^{3}-2t^{2}+t-1.}$ (Notice that ${\displaystyle w(t)}$ is essentially the Jones polynomial for the Whitehead link.)

The HOMFLY polynomial is

${\displaystyle P(\alpha ,z)=z^{-2}\alpha ^{-2}-4z^{2}\alpha ^{-2}-4z^{4}\alpha ^{-2}-z^{6}\alpha ^{-2}-2z^{-2}+8z^{2}+12z^{4}+6z^{6}+z^{8}+z^{-2}\alpha ^{2}-4z^{2}\alpha ^{2}-4z^{4}\alpha ^{2}-z^{6}\alpha ^{2},\,}$

and the Kauffman polynomial is

${\displaystyle {\begin{aligned}F(a,z)&=1+2z^{-2}+a^{-2}z^{-2}+a^{2}z^{-2}-2a^{-1}z^{-1}-az^{-1}-20z^{2}+2a^{-4}z^{2}\\[6pt]&{}-8a^{-2}z^{2}-8a^{2}z^{2}+2a^{4}z^{4}+2a^{4}z^{2}-2a^{-5}z^{3}+4a^{-3}z^{3}+6a^{-1}z^{3}\\[6pt]&{}+6az^{3}+4a^{3}z^{3}-2a^{5}z^{3}+42z^{4}-7a^{-4}z^{4}+14a^{-2}z^{4}\\[6pt]&{}+14a^{2}z^{4}-7a^{4}z^{4}+a^{-5}z^{5}-9a^{-3}z^{5}-2a^{-1}z^{5}-2az^{5}-9a^{3}z^{5}\\[6pt]&{}+a^{5}z^{5}-28z^{6}+3a^{-4}z^{6}-11a^{-2}z^{6}-11a^{2}z^{6}+3a^{4}z^{6}+4a^{-3}z^{7}\\[6pt]&{}-2a^{-1}z^{7}-2az^{7}+4a^{3}z^{7}+8z^{8}+4a^{-2}z^{8}+4a^{2}z^{8}+2a^{-1}z^{9}+2az^{9}.\end{aligned}}}$

Pseudo-symmetric visual variants

David Swart,^[5] and independently Rick Mabry and Laura McCormick,^[6] discovered alternative 12-crossing visual representations of the L10a140 link. In these depictions, the link no longer has strictly alternating crossings (as it does in its simplest 10-crossing form), but there is greater superficial symmetry.

So the leftmost image below shows a 12-crossing link (distinct from both the Borromean rings and the L10a140 link) with six-fold rotational symmetry. The center image shows a similar-looking depiction of the L10a140 link (but without true rotational symmetry). Similarly, the rightmost image shows a depiction of the L10a140 link with superficial fourfold symmetry.

• 
  Fully symmetrical 12-crossing Brunnian link (L12a1882)
• 
  L10a140 in pseudo 6-symmetric form
• 
  L10a140 in pseudo 4-symmetric form

References

External links

Wikimedia Commons has media related to L10a140 links.

• "It Is What It Is", Flickr.com.

This page was last edited on 12 May 2024, at 18:43