 |
 |
| Dualidad entre centros de cara y vértices del dodecaedro y del icosaedro | |
 |
 |
| Dualidad entre centros de cara y vértices del octaedro y del cubo | |
En matemáticas, una dualidad, en términos generales, traduce conceptos, teoremas o estructuras matemáticas en otros conceptos, teoremas o estructuras, mediante una correspondencia uno a uno, a menudo (pero no siempre) por medio de una operación de involución: si el dual de A es B, entonces el dual de B es A. Tales involuciones a veces tienen puntos fijos, de modo que el dual de A es A en sí mismo. Por ejemplo, el teorema de Desargues expresa una condición auto dual en este sentido bajo el concepto de dualidad en geometría proyectiva.
En contextos matemáticos, el término dualidad tiene numerosos significados,[1] aunque es «un concepto muy dominante e importante en matemáticas (modernas)»[2] y «un tema general de gran interés que tiene manifestaciones en casi todas las áreas de las matemáticas».[3]
Muchas dualidades matemáticas entre objetos de dos tipos corresponden a emparejamientos, que mediante operadores bilineales relacionan un objeto de un tipo y otro objeto de un segundo tipo a una familia de escalares. Por ejemplo, la «dualidad en álgebra lineal» se corresponde de esta manera con aplicaciones bilineales de pares de espacios de vectores a escalares, la «dualidad entre distribuciones y las funciones de prueba asociadas» corresponde al emparejamiento en el que se integra una distribución con una función de prueba, y la dualidad de Poincaré corresponde de manera similar al número de intersecciones, visto como un emparejamiento entre subvariedades de una colección de objetos matemáticos determinada.[4]
Desde el punto de vista de la teoría de categorías, la dualidad también se puede ver como un funtor, al menos en el ámbito de los espacios vectoriales. Este funtor asigna a cada espacio su espacio dual, y la construcción de retorno asigna a cada flecha
- f: V → W su dual f∗: W∗ → V∗
En teoría de conjuntos y en lógica matemática el concepto de dualidad también desempeña un papel esencial.
Ejemplos introductorios
En palabras de Michael Atiyah,
La dualidad en matemáticas no es un teorema, sino un «principio».[1]
|
La siguiente lista de ejemplos muestra las características comunes de muchas dualidades, pero también indica que el significado preciso de la dualidad puede variar de un caso a otro.
Complemento de un subconjunto
Una dualidad simple, quizás la más simple, surge de considerar subconjuntos de un conjunto fijo S. Para cualquier subconjunto A ⊆ S, su complemento Ac[5] consta de todos los elementos en S que no están contenidos en A. El resultado es nuevamente un subconjunto de S. Tomar el complemento tiene las siguientes propiedades:
- Al aplicarlo dos veces, se obtiene el conjunto original, es decir, (Ac)c = A. Esto se menciona diciendo que la operación de tomar el complemento es una involución.
- Una inclusión de conjuntos A ⊆ B se convierte en una inclusión en la dirección opuesta Bc ⊆ Ac.
- Dado dos subconjuntos A y B de S, A está contenido en Bc si y solo si B está contenido en Ac.
Esta relación aparece en topología como una dualidad entre subconjuntos abiertos y cerrados de un espacio topológico fijo X: un subconjunto U de X es cerrado si y solo si su complemento en X es abierto. Debido a esto, muchos teoremas sobre conjuntos cerrados son duales a teoremas sobre conjuntos abiertos. Por ejemplo, cualquier unión de conjuntos abiertos es abierta, por lo que cualquier intersección de conjuntos cerrados es cerrada. El interior de un conjunto es el conjunto abierto más grande que contiene, y el cierre del conjunto es el conjunto cerrado más pequeño que contiene. Debido a la dualidad, el complemento del interior de cualquier conjunto U es igual al cierre del complemento de U.
Cono dual
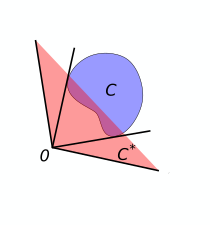
En geometría existe una construcción denominada cono dual: dado un conjunto de puntos en el plano (o más generalmente, puntos en ), su cono dual se define como el conjunto que consiste en sus puntos tales que satisfacen la condición
para todos los puntos en , como se ilustra en el diagrama. A diferencia del complemento de conjuntos mencionado anteriormente, en general no es cierto que la aplicación dos veces de la construcción del cono dual, devuelva el conjunto original . En cambio, es el cono[6] más pequeño que contiene , que puede ser más grande que . Por lo tanto, esta dualidad es más débil que la anterior, verificándose que
- La aplicación de la operación dos veces devuelve un conjunto posiblemente más grande: para todos los , está contenido en . (Para algunos , es decir, para los propios conos, los dos son en realidad iguales).
Las otras dos propiedades se transfieren sin cambios:
- Todavía es cierto que una inclusión se convierte en una inclusión en la dirección opuesta ().
- Dados dos subconjuntos y del plano, está contenido en si y solo si está contenido en .
Espacio vectorial dual
Un ejemplo muy importante de dualidad surge en el álgebra lineal al asociar a cualquier espacio vectorial V su espacio dual V*. Sus elementos son las k-aplicaciones lineales , donde k es el campo sobre el cual se define V. Las tres propiedades del cono dual se transfieren a este tipo de dualidad al reemplazar los subconjuntos de por el espacio vectorial y las inclusiones de dichos subconjuntos por aplicaciones lineales. Es decir:
- La aplicación de la operación de tomar dos veces el espacio vectorial dual produce otro espacio vectorial V**. Siempre existe una aplicación V → V**. Para algunos V, concretamente los espacios vectoriales de dimensión finita, esta aplicación es un isomorfismo.
- Una aplicación lineal V → W da lugar a una aplicación en la dirección opuesta (W* → V*).
- Dados dos espacios vectoriales V y W, las aplicaciones de V a W* se corresponden con las aplicaciones de W a V*.
Una característica particular de esta dualidad es que V y V* son isomórficos para ciertos objetos, a saber, espacios vectoriales de dimensión finita. Sin embargo, esto es, en cierto sentido, una coincidencia afortunada, porque dar un isomorfismo de este tipo requiere una cierta elección, por ejemplo, la elección de una base de V. Esto también es cierto en el caso de que V sea un espacio de Hilbert, a través del teorema de representación de Riesz.
Teoría de Galois
En todas las dualidades discutidas anteriormente, el dual de un objeto es del mismo tipo que el objeto mismo. Por ejemplo, el dual de un espacio vectorial es nuevamente un espacio vectorial. Muchas declaraciones de dualidad no son de este tipo. En cambio, tales dualidades revelan una relación cercana entre objetos de naturaleza aparentemente diferente. Un ejemplo de tal dualidad más general es el de la teoría de Galois. Para una extensión de Galois K / F fija, se puede asociar el grupo de Galois Gal(K/E) a cualquier campo intermedio E (es decir, F ⊆ E ⊆ K). Este grupo es un subgrupo del grupo de Galois G = Gal(K/F). Por el contrario, para cualquier subgrupo H ⊆ G existe el campo fijo KH que consiste en elementos fijados por los elementos en H.
Comparado con lo anterior, esta dualidad tiene las siguientes características:
- Una extensión F ⊆ F′ de campos intermedios da lugar a una inclusión de grupos de Galois en la dirección opuesta: Gal(K/F′) ⊆ Gal(K/F).
- La asociación de Gal(K/E) a E y KH a H es inversa entre sí. Este es el contenido del teorema fundamental de la teoría de Galois.
Dualidades de inversión de órdenes
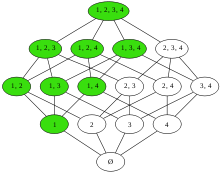
Dado un conjunto parcialmente ordenado P = (X, ≤) (abreviatura de conjunto parcialmente ordenado, es decir, un conjunto que tiene una noción de orden, pero en el que dos elementos no pueden colocarse necesariamente en orden relativo entre sí), el conjunto parcialmente ordenado dual Pd = (X, ≥) comprende el mismo conjunto de suelo pero con la relación transpuesta. Ejemplos familiares de órdenes parciales dobles incluyen;
- Las relaciones subconjunto y superconjunto ⊂ y ⊃ en cualquier colección de conjuntos, como los subconjuntos de un conjunto fijo S. Esto da lugar al primer ejemplo de una dualidad mencionada arriba.
- Las relaciones divisor y múltiplo en los números enteros.
- Las relaciones descendiente de y ancestro de en el conjunto de humanos.
Una "transformación de dualidad" es un antiautomorfismo involutivo f de un conjunto parcialmente ordenado S, es decir, una involución de orden inverso f : S → S.[7][8] En varios casos importantes, estas propiedades simples determinan la transformación de forma única hasta algunas simetrías simples. Por ejemplo, si f1, f2 son dos transformaciones duales, entonces su composición es un automorfismo de orden de S; por lo tanto, cualesquiera dos transformaciones de dualidad difieren solo por un automorfismo de orden. Por ejemplo, todos los automorfismos de un conjunto potencia S = 2R son inducidos por permutaciones de R.
Un concepto definido para un orden parcial P corresponderá a un «concepto dual» en el conjunto parcialmente ordenado dual Pd. Por ejemplo, un elemento minimal de P será un elemento maximal de Pd: la minimización y la maximización son conceptos duales en la teoría del orden. Otros pares de conceptos duales son borde superior e inferior; conjunto inferior y superior; e ideales y filtros.
En topología, conjuntos abiertos y conjuntos cerrados son conceptos duales: el complemento de un conjunto abierto está cerrado, y viceversa. En la teoría matroide, la familia de conjuntos complementarios a los conjuntos independientes de un matroide dado forman ellos mismos otro matroide, llamado matroide dual.
Dualidades de inversión de la dimensión

Existen muchas dualidades distintas pero interrelacionadas en las que los objetos geométricos o topológicos se corresponden con otros objetos del mismo tipo, pero con una inversión de las dimensiones de las características de los objetos. Un ejemplo clásico de esto es la dualidad de los sólidos platónicos, en los cuales el cubo y el octaedro forman un par dual, el dodecaedro y el icosaedro forman otro par dual, y el tetraedro es «autodual». El poliedro conjugado de cualquiera de estos poliedros puede formarse como la envolvente convexa de los puntos centrales de cada cara del poliedro primario, por lo que los vértices del dual se corresponden uno a uno con las caras del primero. De manera similar, cada arista del dual se corresponde a una arista del primario, y cada cara del dual se corresponde con un vértice del primario. Estas correspondencias preservan la relación de incidencia: si dos partes del poliedro primario se tocan entre sí, también lo hacen las dos partes correspondientes del poliedro conjugado. Más generalmente, usando el concepto de reciprocidad polar, cualquier poliedro convexo, o más generalmente cualquier politopo convexo, corresponde a un poliedro conjugado o politopo dual, con una característica i-dimensional de un politopo de dimensión n correspondiente a una característica (n − i − 1)-dimensional del politopo dual. La naturaleza preservadora de la incidencia de la dualidad se refleja en el hecho de que las retículas de cara de los poliedros o politopos primarios y duales son ellas mismas duales de orden teorético. La dualidad de los politopos y la dualidad de orden-teorético son ambas involuciones: el politopo dual del politopo dual de cualquier politopo es el politopo original, y al invertir todas las relaciones de orden dos veces, vuelven al orden original. Elegir un centro de polaridad diferente conduce a politopos duales geométricamente diferentes, pero todos tienen la misma estructura combinatoria.
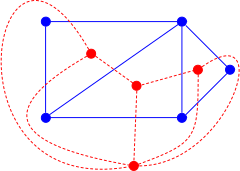
A partir de cualquier poliedro tridimensional, puede formarse un grafo plano: la gráfica de la relación de sus vértices y aristas. El poliedro dual tiene un grafo dual, un gráfico con un vértice para cada cara del poliedro y con una arista por cada dos caras adyacentes. El mismo concepto de dualidad gráfica plana se puede generalizar a gráficos que se dibujan en el plano pero que no provienen de un poliedro tridimensional, o más generalmente a grafos embebidos en superficies correspondientes a elementos de género superior: se puede dibujar un gráfico dual colocando un vértice dentro de cada región delimitada por un recinto de aristas en la gráfica, y dibujando un vínculo que conecte dos regiones cualesquiera que compartan una arista. Un ejemplo importante de este tipo proviene de la geometría computacional: la dualidad para cualquier conjunto finito S de puntos en el plano entre la triangulación de Delaunay de S y los polígonos de Thiessen de S. Al igual que con poliedros duales y politopos duales, la dualidad de gráficos en superficies es una involución de inversión de la dimensión: cada vértice en el gráfico embebido del primario se corresponde con una región del grafo em embebido del dual, cada arista en el primario está cruzada por una arista en el dual, y cada región del primaario se corresponde con un vértice del dual. El grafo dual depende de cómo este embebido el grafo del primario: diferentes embebidos en el plano de un solo grafo pueden conducir a diferentes grafos duales. La dualidad de matroides es una extensión algebraica de la dualidad entre grafos planos, en el sentido de que el matroide dual del matroide gráfico de un grafo plano, es isomorfo al matroide gráfico del grafo dual.
También se produce una especie de dualidad geométrica en la teoría de la optimización, pero no una que invierta las dimensiones. Una programación lineal puede ser especificada por un sistema de variables reales (las coordenadas de un punto en el espacio euclidiano ), un sistema de restricciones lineales (especificando que el punto se encuentre en un semiespacio; la intersección de estos semiespacios es un politopo convexo, la región factible del programa), y una función lineal (que se debe optimizar). Cada programa lineal tiene un problema dual con la misma solución óptima, pero las variables en el problema dual se corresponden a restricciones en el problema primario y viceversa.
Dualidad en lógica y teoría de conjuntos
En lógica, las funciones o relaciones A y B se consideran duales si A(¬x) = ¬B(x), donde el símbolo ¬ indica la negación lógica. La dualidad básica de este tipo es la dualidad de los cuantificadores ∃ y ∀ de la lógica clásica. Estos dos conceptos son duales porque ∃x.¬P(x) y ¬∀x.P(x) son equivalentes para todos los predicados P en la lógica clásica: si existe un x para el cual P no puede afirmarse, entonces es falso que P sea válido para todos los x (pero el inverso no se sostiene de manera constructiva). De esta dualidad lógica fundamental, se deducen otras:
- Se dice que una fórmula es «satisfactoria» en un determinado modelo si hay asignaciones a sus variables libres que la hacen verdadera; es válida si cada asignación a sus variables libres la hacen verdadera. La satisfacibilidad y la validez son dobles porque las fórmulas inválidas son precisamente aquellas cuyas negaciones son satisfactorias, y las fórmulas insatisfactorias son aquellas cuyas negaciones son válidas. Esto puede verse como un caso especial del ítem anterior, con los cuantificadores variando en las interpretaciones.
- En lógica clásica, los operadores ∧ y ∨ son duales en este sentido, porque (¬x ∧ ¬y) y ¬(x ∨ y) son equivalentes. Esto significa que para cada teorema de la lógica clásica existe un teorema dual equivalente. Las leyes de De Morgan son ejemplos. Más generalmente, ∧ (¬ xi) = ¬∨ xi. El lado izquierdo es verdadero si y solo si ∀i.¬xi, y el lado derecho si y solo si ¬∃i.Xi.
- En lógica modal, □ p significa que la proposición p es necesariamente verdadera, y ◊ p que p es posiblemente verdadera. La mayoría de las interpretaciones de la lógica modal asignan significados dobles a estos dos operadores. Por ejemplo, en la semántica de Kripke, «p es posiblemente cierto» significa «existe un W universal tal que p es verdadero en W», mientras que «p es necesariamente verdadero» significa «para todos los universos W, p es verdadero en W». La dualidad de □ y ◊ se sigue de la dualidad análoga de ∀ y ∃. Otros operadores modales duales se comportan de manera similar. Por ejemplo, la lógica temporal tiene operadores que denotan «será cierto en algún momento en el futuro» y «será cierto en todo momento en el futuro», que son igualmente duales.
Otras dualidades análogas se derivan de estas:
- La unión e intersección teórica de conjuntos son duales bajo el operador complemento de un conjunto ⋅C. Es decir, AC ∩ BC = (A ∪ B)C, y más generalmente, ∩ AαC = (∪ Aα)C. Esto se deduce de la dualidad de ∀ y ∃: un elemento x es miembro de ∩ AαC si y solo si es ∀α.¬x ∈ Aα, y es miembro de (∪ Aα)C si y solo si es ¬∃α.x ∈ Aα.
Objetos duales
Un grupo de dualidades se puede describir dotando, para cualquier objeto matemático X, del conjunto de morfismos Hom (X, D) en un objeto fijo D, con una estructura similar a la de X. Esto a veces se llama homomorfismo interno. En general, esto produce una dualidad verdadera solo para elecciones específicas de D, en cuyo caso X* = Hom (X, D) se conoce como el dual de X. Siempre hay una aplicación desde X hasta el bidual, es decir, el dual del dual,
Asigna a x ∈ X la aplucación que asocia a cualquier aplicación f:X → D (es decir, un elemento en Hom(X, D)) el valor f(x). Dependiendo de la dualidad concreta considerada y también dependiendo del objeto X, esta aplicación puede o no ser un isomorfismo.
Espacios vectoriales duales revisados
La construcción del espacio dual de vectores
mencionado en la introducción es un ejemplo de tal dualidad. De hecho, el conjunto de morfismos, es decir, las aplicaciones lineales, forma un espacio vectorial en sí mismo. La aplicación V → V** mencionada anteriormente siempre es inyectiva. Es suprayectiva, y por lo tanto un isomorfismo, si y solo si la dimension de V es finita. Este hecho caracteriza los espacios vectoriales de dimensión finita sin referirse a una base.
Isomorfismos de V y V∗ y espacios con producto interno
Un espacio vectorial V es isomorfo a V∗ precisamente si V es de dimensión finita. En este caso, tal isomorfismo es equivalente a una forma bilineal no degenerada
En este caso, V se llama espacio prehilbertiano. Por ejemplo, si K es el campo de los números reales o de los números complejos, cualquier forma bilineal positiva definida da lugar a dicho isomorfismo. En geometría de Riemann, se toma V como el espacio tangente de una variedad y tales formas bilineales positivas se llaman variedades de Riemann. Su propósito es medir ángulos y distancias. Por lo tanto, la dualidad es una base fundamental de esta rama de la geometría. Otra aplicación de espacios con producto interno es el dual de Hodge, que proporciona una correspondencia entre los elementos del álgebra exterior. Para un espacio vectorial de dimensión n, el operador en estrella de Hodge aplica k-formas en (n − k)-formas. Esta propiedad se puede usar por ejemplo para formular las ecuaciones de Maxwell. De esta forma, la dualidad inherente a un espacio con producto interno permite intercambiar los roles del campo magnético y del campo eléctrico.
Dualidad en geometría proyectiva
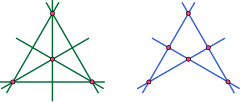
En algunos planos proyectivos, es posible encontrar transformaciones geométricas que apliquen cada punto del plano proyectivo a una línea, y cada línea del plano proy.ectivo a un punto, de forma que se conservan las relaciones de incidencia.[9] Para tales planos surge un principio general de dualidad proyectiva: dado cualquier teorema en dicha geometría proyectiva plana, el intercambio de los términos «punto» y «recta» en todas partes da como resultado un nuevo teorema igualmente válido.[10] Un ejemplo simple es que la afirmación «dos puntos determinan una recta única, que pasa por estos puntos», tiene la declaración dual de que «dos rectas determinan un punto único, el punto de intersección de estas dos líneas rectas». Para ver más ejemplos, véase teoremas duales.
El espacio vectorial dual ofrece una explicación conceptual de este fenómeno en algunos planos (especialmente en los planos de campo). De hecho, los puntos en el plano proyectivo corresponden a subespacios vectoriales unidimensionales,[11] mientras que las líneas en el plano proyectivo corresponden a subespacios vectoriales de dimensión 2. La dualidad en tales geometrías proyectivas se deriva de la asignación a un unidimensional del subespacio de que consiste en esas aplicaciones lineales que satisfacen . Como consecuencia de la fórmula de dimensión del álgebra lineal, este espacio es bidimensional, es decir, corresponde a una línea recta en el plano proyectivo asociado a .
La forma bilineal (definida positiva)
produce una identidad de este plano proyectivo con el . Concretamente, la dualidad asigna a su ortogonal . Las fórmulas explícitas de la dualidad en la geometría proyectiva surgen por medio de esta identidad.
Espacios vectoriales topológicos y espacios de Hilbert
En el ámbito de los espacios vectoriales topológicos, existe una construcción similar, reemplazando el dual por el espacio vectorial dual topológico. Un espacio vectorial topológico que es canónicamente isomorfo a su bidual se llama espacio reflexivo. Por ejemplo, el dual de un espacio-Lp es Lq donde 1/p + 1/q = 1 proporciona ese 1 ≤ p < ∞, pero el dual de L∞ es más grande que L1. Por lo tanto, L1 no es reflexivo.
Los espacios de Hilbert H están equipados con un producto interno 〈-, -〉. Como en el caso de dimensiones finitas, permite definir una aplicación
El teorema de representación de Riesz afirma que esta aplicación es un isomorfismo, es decir, cada espacio de Hilbert es isomorfo a su dual.
Las distribuciones son funcionales lineales sobre espacios de funciones apropiados. Son un medio técnico importante en la teoría de ecuaciones en derivadas parciales: en lugar de resolverlas directamente, puede ser más fácil primero hallar soluciones en el "sentido débil", es decir, encontrar una distribución que las satisfaga y, segundo, demostrar que la solución debe ser, de hecho, una función.[12]
Otros objetos duales
La red recíproca de una retícula L viene dada por
- ,
que se usa en la construcción de variedades tóricas.[13] La dualidad de Pontryagin de compacidad local sobre grupos topológicos G viene dada por
- ,
homomorfismo de grupos continuo con valores en el círculo (con la multiplicación de números complejos como operación de grupo).
Categorías duales
Categoría opuesta y funtores adjuntos
En otro grupo de dualidades, los objetos de una teoría se traducen en objetos de otra teoría y las aplicaciones entre objetos en la primera teoría se traducen en morfismos en la segunda teoría, pero con la dirección invertida. Usando el lenguaje de la teoría de categorías, esto equivale a un funtor entre dos categorías C y D:
- F: C → D
que para dos objetos cualesquiera X e Y de C da una aplicación
- HomC(X, Y) → HomD(F(Y), F(X))
Ese funtor puede ser o no ser una equivalencia de categorías. Hay varias situaciones, donde dicho funtor es una equivalencia entre una categoría opuesta Cop de C y D. Utilizando una dualidad de este tipo, cada enunciado de la primera teoría puede traducirse en una declaración dual en la segunda teoría, donde la dirección de todas las flechas debe invertirse.[14] Por lo tanto, cualquier dualidad entre las categorías C y D es formalmente la misma que una equivalencia entre C y Dop (Cop y D). Sin embargo, en muchas circunstancias, las categorías opuestas no tienen un significado inherente, lo que hace que la dualidad sea un concepto adicional separado.[15]
Una categoría que es equivalente a su dual se llama auto-dual. Un ejemplo de categoría autodual es la categoría de los espacios de Hilbert.[16]
Muchas nociones de teoría de categorías vienen en pares en el sentido de que se corresponden entre sí al considerar la categoría opuesta. Por ejemplo, el producto cartesiano Y1 × Y2 y la unión disjunta Y1 ⊔ Y2 de conjuntos son duales entre sí en el sentido de que
- Hom (X, Y1 × Y2) = Hom (X, Y1) × Hom (X, Y2)
y
- Hom (Y1 ⊔ Y2, X) = Hom (Y1, X) × Hom (Y2, X)
para cualquier conjunto X. Este es un caso particular de un fenómeno de dualidad más general, según el cual los límites en una categoría C corresponde al límite en la categoría opuesta Cop; otros ejemplos concretos de esto son los epimorfismo frente a los monomorfismos; el módulo factor en relación con el módulo; el producto directo frente a la suma directa (también llamado coproducto para enfatizar el aspecto de dualidad). Por lo tanto, en algunos casos, las pruebas de ciertas declaraciones se pueden reducir a la mitad, utilizando dicho fenómeno de dualidad. Otras nociones que muestran una dualidad categórica relacionada son el módulo proyectivo y el módulo inyectivo en álgebra homológica,[17] la fibración y la cofibración en topología y, en general, a la categoría de modelos.[18]
Dos funtores F: C → D y G: D → C son adjuntos si para todos los objetos c en C y d en D
- HomD(F(c), d) ≅ HomC(c, G(d)),
de forma natural. En realidad, la correspondencia de límites y colímites es un ejemplo de adjuntos, ya que hay una adjunción
- colim: CI ↔ C: Δ
del funtor colímite que asigna a cualquier diagrama en C indexado por alguna categoría I su colímite y el funtor diagonal que asigna cualquier objeto c de C al diagrama constante que tiene c en todos los lugares. Dualmente,
- Δ: C ↔ CI: lim.
Espacios y funciones
La dualidad de Gelfand es una dualidad entre C*-álgebras conmutativas A y espacios de Hausdorff compactos X con las mismas características: asigna a X el espacio de funciones continuas (que desaparecen en el infinito) de X a C, los números complejos. Por el contrario, el espacio X se puede reconstruir a partir de A como el espectro de A. Tanto la dualidad de Gelfand como la de Pontryagin se pueden deducir de una manera en gran parte formal, principalmente teórica, por categorías.[19]
En una línea similar hay una dualidad en geometría algebraica entre anillos conmutativos y sus espectros: para cada anillo conmutativo A hay un espectro afín, Espec A. Por el contrario, dado un esquema afín S, se recupera un anillo tomando secciones globales del espacio localmente anillado OS. Además, los homomorfismo de anillos están en correspondencia uno a uno con morfismos de esquemas afines, y por lo tanto hay una equivalencia
- (Anillos conmutativos)op ≅ (esquemas afines)[20]
Los esquemas de afinidad son los componentes locales de estos esquemas. El resultado anterior, por lo tanto, dice que la teoría local de los esquemas es la misma que el álgebra conmutativa, el estudio de los anillos conmutativos.
La geometría no conmutativa se inspira en la dualidad de Gelfand y estudia las C*-algebras no conmutativas como si fueran funciones en un espacio imaginario. La dualidad de Tannaka-Krein es un análogo no-conmutativo de la dualidad de Pontryagin.[21]
Conexiones de Galois
En una serie de situaciones, las dos categorías que son duales entre sí surgen realmente de los conjuntos parcialmente ordenados, es decir, existe una noción de que un objeto es "más pequeño" que otro. Una dualidad que respeta los citados conceptos se conoce como una conexión de Galois. Un ejemplo es la dualidad estándar en la teoría de Galois mencionada en la introducción: una extensión de campo más grande corresponde -bajo la aplicación que asigna a cualquier extensión L ⊃ K (dentro de un campo fijo más grande Ω) el grupo de Galois Gal (Ω/L) - a un grupo más pequeño.[22]
La colección de todos los subconjuntos abiertos de un espacio topológico X forma un álgebra de Heyting completa. Existe una dualidad, conocida como dualidad de Stone, que conecta espacios sobrios y espacios locales.
- El teorema de representación de Birkhoff está relacionado con retículos distributivos y con conjuntos parcialmente ordenados.
Dualidad de Pontryagin
La dualidad de Pontryagin se aplica sobre la categoría de grupos abelianos de compacidad local: dado cualquier grupo G de ese tipo, el grupo carácter
- χ (G) = Hom (G, S1)
dado por los homomorfismos grupales continuos de G sobre el grupo circular S1 puede ser dotado con una topología abierta compacta. La dualidad de Pontryagin afirma que el grupo de caracteres es de nuevo localmente compacto abeliano y que
- G ≅ χ (χ (G)).[23]
Además, los grupos discretos corresponden a grupos compactos abelianos; los grupos finitos corresponden a grupos finitos. Por un lado, la dualidad de Pontryagin es un caso especial de dualidad de Gelfand. Por otro lado, es la razón conceptual del análisis de Fourier, que figura a continuación.
Dualidades analíticas
En análisis, los problemas se resuelven con frecuencia pasando a la descripción dual de funciones y operadores.
La transformada de Fourier alterna entre funciones en un espacio vectorial y su dual:
y por el contrario
Si f es una función L2 en R o RN, por ejemplo, entonces también lo son y . Además, la transformación intercambia operaciones de multiplicación y convolución en los espacios funcionales correspondientes. Una explicación conceptual de la transformada de Fourier se obtiene mediante la dualidad de Pontryagin antes mencionada, aplicada a los grupos localmente compactos R (o R N etc.): cualquier carácter de R está dado por ξ↦ e−2πixξ. El carácter dualizante de la transformada de Fourier tiene muchas otras manifestaciones, por ejemplo, en las descripciones alternativas de los sistemas de mecánica cuántica en términos de representaciones de coordenadas y momento.
- La transformada de Laplace es similar a la transformada de Fourier e intercambia operadores de multiplicación polinómicos, por operadores diferenciales con coeficientes constantes.
- La transformada de Legendre es una dualidad analítica importante que alterna entre velocidades en mecánica lagrangiana y momentos en mecánica hamiltoniana.
Homología y cohomología
Los teoremas que muestran que ciertos objetos de interés son los espacios duales (en el sentido del álgebra lineal) de otros objetos de interés a menudo se llaman dualidades. Muchas de estas dualidades están dadas por un operador bilineal de dos K-espacios vectoriales
- A ⊗ B → K .
Para formas bilineales, hay, por lo tanto, un isomorfismo de A al dual de B.
Dualidad de Poincaré
La dualidad de Poincaré de una variedad compleja compacta y uniforme X está dada por un emparejamiento de cohomología singular con C-coeficientes (equivalentemente, el haz cohomólogo del haz constante C)
- Hi (X) ⊗ H2n−i (X) → C,
donde n es la dimensión (compleja) de X.[24] La dualidad de Poincaré también se puede expresar como una relación de homología singular y de cohomología de De Rham, al afirmar que la aplicación
(integrando una forma diferencial k sobre un ciclo 2n−k-(real)-dimensional) es un emparejamiento perfecto.
La dualidad de Poincaré también invierte dimensiones; corresponde al hecho de que, si una variedad topológica se representa como un cW-complejo, entonces el dual del complejo (una generalización de mayor dimensión del gráfico planar dual) representa la misma variedad. En la dualidad de Poincaré, este homeomorfismo se refleja en un isomorfismo del grupo homología y del grupo cohomología.
Dualidad en geometría algebraica y aritmética
El mismo patrón de dualidad se cumple para una variedad projectiva uniforme sobre una clausura algebraica, utilizando una cohomología l-ádica con coeficientes Qℓ en su lugar.[25] Esto se generaliza más en las variedades singulares, usando cohomología de intersección, una dualidad llamada dualidad de Verdier.[26] La dualidad de Serre o dualidad coherente son similares a las declaraciones anteriores, pero se aplica a la cohomología de haces coherentes en su lugar.[27]
Con el aumento del nivel de generalidad, resulta que una cantidad cada vez mayor de conocimientos técnicos es útil o necesaria para comprender estos teoremas: la formulación moderna de estas dualidades se puede llevar a cabo utilizando categorías derivadas y ciertos funtores de haces directos e inversos (con respecto a la topología analítica clásica de variedades para la dualidad de Poincaré, haces l-ádicos y topología de propagación en el segundo caso, y con respecto a haces coherentes para la dualidad coherente).
Otro grupo de declaraciones de dualidad similares se encuentra en la aritmética: la cohomología de propagación finita, local y de campos globales (también conocida como cohomología de Galois, ya que la cohomología de propagación sobre un campo es equivalente a la cohomología de grupo del campo del grupo de Galois absoluto) admite emparejamientos similares. El grupo de Galois absoluto G (F q) de un campo finito, por ejemplo, es isomorfo a , el grupo profinito de Z, los números enteros. Por lo tanto, el emparejamiento perfecto (para cualquier <i>G</i>-módulo M)
- Hn (G, M) × H1−n (G, Hom (M, Q/Z)) → Q/Z [28]
es una consecuencia directa de la dualidad de Pontryagin de grupos finitos. Para los campos locales y globales, existen sentencias similares (como la dualidad local de Tate y la dualidad de Poitou-Tate).[29]
Véase también
- Anexo:Lista de dualidades
- Dual (teoría de categorías)
- Categoría autónoma
- Norma dual
- Número dual, para cierta álgebra asociativa. El término dual aquí es sinónimo de doble, y no está relacionado con las nociones dadas anteriormente.
- Dualidad (circuitos eléctricos)
- Dualidad (optimización)
- Dualidad de Koszul
- Dual de Langlands
- Dualidad de Petrie
- Dualidad-T, Simetría especular
- Dualidad-S
- Programación lineal
- Código dual
- Red recíproca
- Base dual
- Variedad abeliana dual
- Funtores adjuntos
- Módulo dualizador
- Dualidad de Matlis
- Haz dualizador
Referencias
- ↑ a b Atiyah, 2007
- ↑ Kostrikin, 2001[página requerida]
- ↑ Gowers, 2008, p. 187, col. 1
- ↑ Gowers, 2008, p. 189, col. 2
- ↑ Para referirse al complemento, a veces se usa la notación S \ A.
- ↑ Más precisamente, es el cono cerrado convexo más pequeño que contiene .
- ↑ Artstein-Avidan y Milman, 2007
- ↑ Artstein-Avidan y Milman, 2008
- ↑ Veblen y Young, 1965.
- ↑ (Veblen y Young, 1965, p. Ch. I, Theorem 11)
- ↑ Más generalmente, se pueden considerar los planos proyectivos sobre cualquier campo, como el de los números complejos, cuerpos finitos o anillos de división.
- ↑ Véase regularidad elíptica.
- ↑ (Fulton, 1993)
- ↑ Mac Lane, 1998, Ch. II.1.
- ↑ (Lam, 1999, p. §19C)
- ↑ Jiří Adámek; J. Rosicky (1994). Locally Presentable and Accessible Categories. Cambridge University Press. p. 62. ISBN 978-0-521-42261-1.
- ↑ (Weibel , 1994)
- ↑ (Dwyer y Spaliński, 1995)
- ↑ Negrepontis, 1971.
- ↑ (Hartshorne, 1966, p. Ch. II.2, esp. Prop. II.2.3)
- ↑ (Joyal y Street, 1991)
- ↑ Véase (Lang, 2002, p. Theorem VI.1.1) para extensiones finitas de Galois.
- ↑ (Loomis, 1953, p. 151, section 37D)
- ↑ (Griffiths y Harris, 1994, p. 56)
- ↑ (Milne, 1980, p. Ch. VI.11)
- ↑ (Iversen, 1986, p. Ch. VII.3, VII.5)
- ↑ (Hartshorne, 1966, p. Ch. III.7)
- ↑ (Milne, 2006, p. Example I.1.10)
- ↑ (Mazur, 1973); (Milne, 2006)
Bibliografía
Dualidad en general
- Atiyah, Michael (2007), Duality in Mathematics and Physics, notas de la conferencia del Institut de Matematica de la Universitat de Barcelona (IMUB).
- Kostrikin, A. I. (2001), «Dualidad (matemática)», en Hazewinkel, Michiel, ed., Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104..
- Gowers, Timothy (2008), «III.19 Duality», The Princeton Companion to Mathematics, Princeton University Press, pp. 187-190..
- Cartier, Pierre (2001), «A mad day's work: from Grothendieck to Connes and Kontsevich. The evolution of concepts of space and symmetry», American Mathematical Society. Bulletin. New Series 38 (4): 389-408, ISSN 0002-9904, MR 1848254, doi:10.1090/S0273-0979-01-00913-2. (una descripción no técnica sobre varios aspectos de la geometría, incluidas las dualidades)
Dualidad en topología algebraica
- James C. Becker y Daniel Henry Gottlieb, Una historia de la dualidad en la topología algebraica
Dualidades específicas
- Artstein-Avidan, Shiri; Milman, Vitali (2008), «The concept of duality for measure projections of convex bodies», Journal of Functional Analysis 254 (10): 2648-2666, doi:10.1016/j.jfa.2007.11.008.. También sitio del autor.
- Artstein-Avidan, Shiri; Milman, Vitali (2007), «A characterization of the concept of duality», Electronic research announcements in mathematical sciences 14: 42-59, archivado desde el original el 24 de julio de 2011, consultado el 8 de agosto de 2011.. También sitio del autor.
- Dwyer, William G.; Spaliński, Jan (1995), «Homotopy theories and model categories», Handbook of algebraic topology, Ámsterdam: North-Holland, pp. 73-126, MR 1361887, archivado desde el original el 9 de febrero de 2021, consultado el 8 de agosto de 2011.
- Fulton, William (1993), Introduction to toric varieties, Princeton University Press, ISBN 978-0-691-00049-7.
- Griffiths, Phillip; Harris, Joseph (1994), Principles of algebraic geometry, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-05059-9, MR 1288523.
- Hartshorne, Robin (1966), Residues and Duality, Lecture Notes in Mathematics 20, Berlin, New York: Springer Science+Business Media, pp. 20-48.
- Hartshorne, Robin (1977), Algebraic Geometry, Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-90244-9, MR 0463157, OCLC 13348052.
- Iversen, Birger (1986), Cohomology of sheaves, Universitext, Berlin, New York: Springer Science+Business Media, ISBN 978-3-540-16389-3, MR 842190.
- Joyal, André; Street, Ross (1991), «An introduction to Tannaka duality and quantum groups», Category theory (Como, 1990), Lecture Notes in Mathematics 1488, Berlin, New York: Springer Science+Business Media, pp. 413-492, MR 1173027.
- Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-98428-5, MR 1653294.
- Lang, Serge (2002), Álgebra, Graduate Texts in Mathematics 211, Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-95385-4, MR 1878556.
- Loomis, Lynn H. (1953), An introduction to abstract harmonic analysis, Toronto-New York-London: D. Van Nostrand Company, Inc., pp. x+190.
- Mac Lane, Saunders (1998), Categories for the Working Mathematician (2nd edición), Berlin, New York: Springer Science+Business Media, ISBN 978-0-387-98403-2.
- Mazur, Barry (1973), «Notes on étale cohomology of number fields», Annales Scientifiques de l'École Normale Supérieure, Série 4 6: 521-552, ISSN 0012-9593, MR 0344254.
- Milne, James S. (1980), Étale cohomology, Princeton University Press, ISBN 978-0-691-08238-7.
- Milne, James S. (2006), Arithmetic duality theorems (2nd edición), Charleston, South Carolina: BookSurge, LLC, ISBN 978-1-4196-4274-6, MR 2261462.
- Negrepontis, Joan W. (1971), «Duality in analysis from the point of view of triples», Journal of Algebra 19 (2): 228-253, ISSN 0021-8693, MR 0280571, doi:10.1016/0021-8693(71)90105-0.
- Veblen, Oswald; Young, John Wesley (1965), Projective geometry. Vols. 1, 2, Blaisdell Publishing Co. Ginn and Co. New York-Toronto-London, MR 0179666.
- Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge University Press, ISBN 978-0-521-55987-4, MR 1269324.




































