Локально тривиальное расслоение — расслоение, которое локально выглядит как прямое произведение.
Определение
Пусть , и — топологические пространства. Сюръективное непрерывное отображение называется локально тривиальным расслоением пространства над базой со слоем , если для всякой точки базы существует окрестность , над которой расслоение тривиально. Последнее означает, что существует гомеоморфизм , такой что коммутативна диаграмма
Здесь — проекция произведения пространств на первый сомножитель.
Пространство также называется тотальным пространством расслоения, или расслоенным пространством.
Связанные определения
- Сечение расслоения — это отображение , такое что . Вообще говоря, не каждое расслоение имеет сечение. Например, пусть — многообразие, а — подрасслоение векторов единичной длины в касательном расслоении . Тогда сечение расслоения — это векторное поле без нулей на . Теорема о причёсывании ежа показывает, что на сфере такого поля не существует.
- Множество называется слоем расслоения над точкой . Каждый слой гомеоморфен пространству , поэтому пространство называется общим (или модельным) слоем расслоения ,
- Гомеоморфизм , отождествляющий ограничение расслоения над окрестностью точки с некоторым тривиальным расслоением, называется локальной тривиализацией расслоения над окрестностью точки .
- Если — покрытие базы открытыми множествами, и — соответствующие им отображения тривиализации, тогда семейство называется тривиализующим атласом расслоения .
- Предположим локально тривиальное расслоение снабжено покрытием базы с выделенной тривиализацией и сужение любого отображения сличения на слой принадлежит некоторой подгруппе группы всех автоморфизмов . Тогда называется локально тривиальным расслоением со структурной группой .
Примеры
- Тривиальное расслоение, то есть проекция на первый сомножитель.
- Любое накрытие является локально тривиальным расслоением с дискретным слоем.
- Касательное, кокасательное и тензорные расслоения над произвольным многообразием локально тривиальны.
- Если — топологическая группа, а — её замкнутая подгруппа, причём факторизация имеет локальные сечения, то является расслоением со слоем (Steenrod 1951, §7).
- Лист Мёбиуса — пространство нетривиального расслоения над окружностью.
- Расслоение Хопфа — это нетривиальное расслоение . Оно не имеет сечений, так как оно является главным расслоением со структурной группой , а любое главное расслоение, допускающее сечение, тривиально.
- Сконструировать расслоение можно, задав произвольно его базу (пространство ), общий слой (пространство ) и отображения перехода (1-коцикл Чеха ) для какого-нибудь открытого покрытия пространства . Тогда пространство E формально можно получить как множество троек вида с правилом отождествления:
- , если
Свойства
- Для локально тривиальных расслоений верна теорема о накрывающей гомотопии. Пусть заданы — локально тривиальное расслоение, отображения и , так что , и гомотопия отображения (то есть ). Тогда существует гомотопия отображения , такая что , то есть следующая диаграмма коммутативна
- Пусть имеется локально тривиальное расслоение со слоем (иногда записываемое формально как ). Тогда последовательность гомотопических групп точна:
- Отображения перехода удовлетворяют условию 1-коцикла Чеха:
- Если , то .
- Два расслоения над одной и той же базой и с одним и тем же общим слоем изоморфны тогда и только тогда, когда 1-коциклы Чеха, соответствующие им, когомологичны. (Отметим, что в случае, когда группа некоммутативна, одномерные когомологии не образуют группу, а образуют множество, на котором действует (слева) группа 0-коцепей Чеха :
- ,
- где — 0-коцепь Чеха, действующая на 1-коцикл Чеха . 1-коциклы называются когомологичными, если они лежат в одной орбите этого действия.)
- Для любого локально тривиального расслоения и непрерывного отображения индуцированное расслоение является локально тривиальным.
Вариации и обобщения
- Локально тривиальные расслоения являются частным случаем
- Если пространства — гладкие (дифференцируемые) многообразия, отображение — гладкое и допускающее тривиализующий атлас с гладкими отображениями тривиализации, то само расслоение называется гладким расслоением.
- Расслоение называется голоморфным, если пространства — комплексные многообразия, отображение — голоморфное и существует тривиализующий атлас с голоморфными отображениями тривиализации.
- Главное расслоение.
См. также
Литература
- Васильев В. А. Введение в топологию. — М.: ФАЗИС, 1997. — 132 с. — ISBN 5-7036-0036-7.
- Steenrod, Norman (1951), The Topology of Fibre Bundles, Princeton University Press, ISBN 0-691-08055-0
Обычно почти сразу, изредка в течении часа.








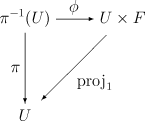





























![{\tilde g}\colon M\times [0;1]\to B](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d5bb1819097f4c25da54bb555a7672b1cf6ce76)


![{\tilde f}\colon M\times [0;1]\to E](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcba9e26b44e19e5a65f92062ad0603758a4e120)


![{\begin{matrix}M\times [0;1]\!&&{\stackrel {{\tilde f}}{\longrightarrow }}\!&&E\\\\&&{\tilde g}\searrow &&\downarrow \pi \\\\&&&&B\end{matrix}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88127bc0c24b514015f57ff09f16ceba053e25ff)














