Плосконосый многогранник — это многогранник, полученный альтернированием (частичным усечением) соответствующего всеусечённого или усечённого многогранника, в зависимости от определения. Некоторые (не все) авторы включают в плосконосые многогранники антипризмы, так как они получаются таким построением из вырожденного «многогранника» всего с двумя гранями (диэдра).
Хиральные плосконосые многогранники не всегда имеют зеркальную симметрию, а потому имеют две зеркальносимметричные формы, которые являются зеркальным отражением друг друга. Их группы симметрии все являются точечными группами.
Например, плосконосый куб:

|

|
Плосконосые многогранники имеют символ Витхоффа |p q r и, при расширении, конфигурацию вершины 3.p.3.q.3.r. Обратноплосконосые многогранники (подмножество плосконосых многогранников, содержащие большой икосаэдр, малый обратноплосконосый икосододекаэдр и большой обратноплосконосый икосододекаэдр), также имеют эту форму символа Витхоффа, но их конфигурация вершин вместо этого равна (3.−p.3.−q.3.−r)/2.
Список плосконосых многогранников
Однородные
Существует 12 однородных плосконосых многогранников, не включая антипризм, икосаэдра как плосконосого тетраэдра, большого икосаэдра как обратноплосконого тетраэдра и большого биплосконосого биромбоикосододекаэдра, известного также как тело Скиллинга.
Когда треугольник Шварца плосконосого многогранника является равнобедренным, плосконосый многогранник не является хиральным. Это имеет место для антипризм, икосаэдра, большого икосаэдра, малого плосконосого икосоикосододекаэдра и малого обратноплосконосого икосододекаэдра.
На рисунке показан результат операции «Snub» (показан искривлённый плосконосый многогранник, топологически эквивалентный однородной версии, полученной из геометрического альтернирования родительского однородного всеусечённого многогранника). Где зелёные грани отсутствуют, грани, полученные путём альтернации, окрашены в красный и жёлтый цвета, а треугольники отреза окрашены в синий цвет. Там, где зелёные грани присутствуют (только для плосконосого икосододекододекаэдра и большого плосконосого додекоикосододекаэдра), грани, полученные альтернацией, окрашены в красный, жёлтый и синий цвета, в то время как треугольники отреза окрашены в зелёный цвет.
| Плосконосый многогранника | Рисунок | Исходный всеусечённый многогранник | Рисунок | Результат операции «Snub» | Группа симметрии | Символ Витхоффа Описание вершин |
|---|---|---|---|---|---|---|
| Икосаэдр (плосконосый тетраэдр) | 
|
Усечённый октаэдр | 
|
|
Ih (Th) | | 3 3 2 3.3.3.3.3 |
| Большой икосаэдр (обратноплосконосый тетраэдр) | 
|
Усечённый октаэдр | 
|
|
Ih (Th) | | 2 3/2 3/2 (3.3.3.3.3)/2 |
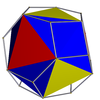
| Плосконосый куб или плосконосый кубооктаэдр |

|
Усечённый кубооктаэдр | 
|
|
O | | 4 3 2 3.3.3.3.4 |
| Плосконосый додекаэдр или плосконосый икосододекаэдр |

|
Усечённый икосододекаэдр | 
|

|
I | | 5 3 2 3.3.3.3.5 |
| Малый плосконосый икосоикосододекаэдр | 
|
Двукратно накрытый усечённый икосаэдр | 
|

|
Ih | | 3 3 5/2 3.3.3.3.3.5/2 |
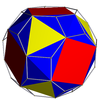
| Плосконосый додекододекаэдр | 
|
Малый ромбододекаэдр с дополнительными 12{10/2} гранями | 
|

|
I | | 5 5/2 2 3.3.5/2.3.5 |
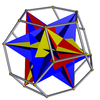
| Плосконосый икосододекододекаэдр | 
|
Икосоусечённый додекододекаэдр | 
|
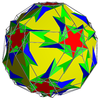
|
I | | 5 3 5/3 3.5/3.3.3.3.5 |
| Большой плосконосый икосододекаэдр | 
|
Ромбоикосаэдр с дополнительными 12{10/2} гранями | 
|

|
I | | 3 5/2 2 3.3.5/2.3.3 |
| Вывернутый плосконосый додекододекаэдр | 
|
Усечённый додекододекаэдр | 
|

|
I | | 5 2 5/3 3.5/3.3.3.3.5 |
| Большой плосконосый додекоикосододекаэдр | 
|
Большой додекоикосаэдр с дополнительными 12{10/2} гранями | 
|
нет рисунка | I | | 3 5/2 5/3 3.5/3.3.5/2.3.3 |
| Большой вывернутый плосконосый икосододекаэдр | 
|
Большой усечённый икосододекаэдр | 
|

|
I | | 3 2 5/3 3.5/3.3.3.3 |
| Малый обратноплосконосый икосододекаэдр | 
|
Двукратно накрытый усечённый икосаэдр | 
|
нет рисунка | Ih | | 5/2 3/2 3/2 (3.3.3.3.3.5/2)/2 |
| Большой обратноплосконосый икосододекаэдр | 
|
Большой ромбододекаэдр с дополнительными 20{6/2} гранями | 
|
нет рисунка | I | | 2 5/3 3/2 (3.3.3.5/2.3)/2 |
| Большой биромбоикосододекаэдр | 
|
— | — | — | Ih | | 3/2 5/3 3 5/2 (4.3/2.4.5/3.4.3.4.5/2)/2 |
| большой биплосконосый биромбоикосододекаэдр | 
|
— | — | — | Ih | | (3/2) 5/3 (3) 5/2 (3/2.3/2.3/2.4.5/3.4.3.3.3.4.5/2.4)/2 |
Примечания:
- В списке только три выпуклых тела — Икосаэдр, плосконосый куб и плосконосый додекаэдр. Они получаются отсечением вершин от усечённого октаэдра, усечённого кубооктаэдра и усечённого икосододекаэдра — трёх выпуклых усечённых квазиправильных многогранников.
- Единственным плосконосым многогранником с хиральной октаэдральной группой симметрии является плосконосый куб.
- Только икосаэдр и большой икосаэдр являются также правильными многогранниками. Они также являются дельтаэдрами.
- Только икосаэдр, большой икосаэдр, малый плосконосый икосоикосододекаэдр, малый обратноплосконосый икосододекаэдр, большой биромбоикосододекаэдр и большой биплосконосый биромбоикосододекаэдр имеют также зеркальные симметрии.
Существует также бесконечное множество антипризм. Они образуются из призм, усечённых осоэдров, вырожденных правильных многогранников. Многогранники до шестиугольных перечислены ниже. На рисунках показан результат операции «Snub», грани, полученные альтернацией (оснований призмы) показаны красным цветом, а треугольники, полученные в результате отсечения, показаны жёлтым. Исключением является тетраэдр, у которого все грани показаны как красные треугольники отсечения, поскольку альтернация квадратных оснований куба приводит к вырожденным двуугольникам в качестве граней.
| Плосконосый многогранник | Рисунок | Исходный всеусечённый многогранник | Рисунок | Плосконосый вариант | Группа симметрии | Символ Витхоффа Описание вершин |
|---|---|---|---|---|---|---|
| Тетраэдр | 
|
Куб | 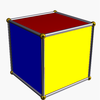
|

|
Td (D2d) | | 2 2 2 3.3.3 |
| Октаэдр | 
|
Шестиугольная призма | 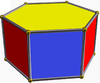
|
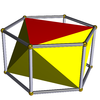
|
Oh (D3d) | | 3 2 2 3.3.3.3 |
| Квадратная антипризма | 
|
Восьмиугольная призма | 
|
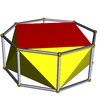
|
D4d | | 4 2 2 3.4.3.3 |
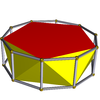
| Пятиугольная антипризма | 
|
Десятиугольная призма | 
|
|
D5d | | 5 2 2 3.5.3.3 |
| Пентаграммная антипризма | 
|
Дважды накрытая пятиугольная призма | 
|

|
D5h | | 5/2 2 2 3.5/2.3.3 |
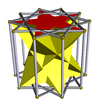
| Пентаграммная скрещенная антипризма | 
|
Декаграммная призма | 
|
|
D5d | | 2 2 5/3 3.5/3.3.3 |
| Шестиугольная антипризма | 
|
Двенадцатиугольная призма | 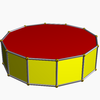
|
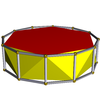
|
D6d | | 6 2 2 3.6.3.3 |
Примечания:
- Два из этих многогранников можно построить из первых двух плосконосых многогранников в списке выше, начинающемся с икосаэдра: пятиугольная антипризма является дважды противоположно отсеченным икосаэдром, а пентаграммная скрещенная антипризма является дважды противоположно отсеченным большим икосаэдром.
Неоднородные
Два правильногранных многогранника являются плосконосыми многогранниками: плосконосый двуклиноид и плосконосая квадратная антипризма. Ни один из этих многогранников не является хиральным.
| Плосконосый многогранник | Рисунок | Исходный многогранник | Рисунок | Группа симметрии |
|---|---|---|---|---|
| Плосконосый двуклиноид | 
|
Равногранный тетраэдр | 
|
D2d |
| Плосконосая квадратная антипризма | 
|
Квадратная антипризма | 
|
D4d |
Примечания
Литература
- Harold Scott MacDonald Coxeter, Longuet-Higgins M. S., Miller J. C. P. Uniform polyhedral // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — 1954. — Т. 246. — С. 401–450. — ISSN 0080-4614. — doi:10.1098/rsta.1954.0003. — .
- Magnus Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — ISBN 0-521-09859-9.
- М. Веннинджер. Модели многогранников. — М.: «Мир», 1974.
- Skilling J. The complete set of uniform polyhedral // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — 1975. — Т. 278. — С. 111–135. — ISSN 0080-4614. — doi:10.1098/rsta.1975.0022. — .
- Mäder R. E. Uniform Polyhedra // Mathematica J.. — 1993. — Т. 3. — С. 48—57.
| Основа | Усечение | Полное усечение | Глубокое усечение | Двойствен- ность |
Растяжение | Всеусечение | Альтернация | ||
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

| ||
| t0{p, q} {p, q} |
t<sub>01</sub>{p,q} t{p, q} |
t1{p,q} r{p, q} |
t<sub>12</sub>{p,q} 2t{p, q} |
t2{p, q} 2r{p, q} |
t<sub>02</sub>{p,q} rr{p, q} |
t<sub>012</sub>{p,q} tr{p, q} |
ht<sub>0</sub>{p,q} h{q, p} |
ht12{p,q} s{q, p} |
ht012{p,q} sr{p, q} |
Обычно почти сразу, изредка в течении часа.
