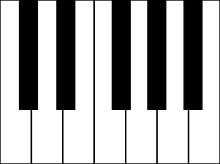
The chromatic scale (or twelve-tone scale) is a set of twelve pitches (more completely, pitch classes) used in tonal music, with notes separated by the interval of a semitone. Chromatic instruments, such as the piano, are made to produce the chromatic scale, while other instruments capable of continuously variable pitch, such as the trombone and violin, can also produce microtones, or notes between those available on a piano.
Most music uses subsets of the chromatic scale such as diatonic scales. While the chromatic scale is fundamental in western music theory, it is seldom directly used in its entirety in musical compositions or improvisation.
YouTube Encyclopedic
-
1/5Views:85 93118 04273 89448 8183 328
-
Singing The Chromatic Scale (with Curwen Hand Signs)
-
What is a Chromatic Scale? Music Theory Lessons - Robert Estrin
-
Can a chromatic scale solo sound cool?
-
Chromatic scale ascending and descending
-
Music Theory 101 - What is Chromatic?
Transcription
Definition
The chromatic scale is a musical scale with twelve pitches, each a semitone, also known as a half-step, above or below its adjacent pitches. As a result, in 12-tone equal temperament (the most common tuning in Western music), the chromatic scale covers all 12 of the available pitches. Thus, there is only one chromatic scale.[a] The ratio of the frequency of one note in the scale to that of the preceding note is given by .[1]
In equal temperament, all the semitones have the same size (100 cents), and there are twelve semitones in an octave (1200 cents). As a result, the notes of an equal-tempered chromatic scale are equally-spaced.
The chromatic scale...is a series of half steps which comprises all the pitches of our [12-tone] equal-tempered system.
— Allen Forte (1979)[2]
All of the pitches in common use, considered together, constitute the chromatic scale. It is made up entirely of successive half steps, the smallest interval in Western music....Counting by half steps, an octave includes twelve different pitches, white and black keys together. The chromatic scale, then, is a collection of all the available pitches in order upward or downward, one octave's worth after another.
— Walter Piston (1987)[3]
A chromatic scale is a nondiatonic scale consisting entirely of half-step intervals. Since each tone of the scale is equidistant from the next [symmetry] it has no tonic [key].[4] ...
Chromaticism [is t]he introduction of some pitches of the chromatic scale into music that is basically diatonic in orientation, or music that is based on the chromatic scale instead of the diatonic scales.[5]— Benward & Saker (2003)
The ascending and descending chromatic scale is shown below.[4]


The twelve notes of the octave—all the black and white keys in one octave on the piano—form the chromatic scale. The tones of the chromatic scale (unlike those of the major or minor scale) are all the same distance apart, one half step. The word chromatic comes from the Greek chroma, color; and the traditional function of the chromatic scale is to color or embellish the tones of the major and minor scales. It does not define a key, but it gives a sense of motion and tension. It has long been used to evoke grief, loss, or sorrow. In the twentieth century it has also become independent of major and minor scales and is used as the basis for entire compositions.
— Roger Kamien (1976)[6]
Notation

The chromatic scale has no set enharmonic spelling that is always used. Its spelling is, however, often dependent upon major or minor key signatures and whether the scale is ascending or descending. In general, the chromatic scale is usually notated with sharp signs when ascending and flat signs when descending. It is also notated so that no scale degree is used more than twice in succession (for instance, G♭ – G♮ – G♯).
Similarly, some notes of the chromatic scale have enharmonic equivalents in solfege. The rising scale is Do, Di, Re, Ri, Mi, Fa, Fi, Sol, Si, La, Li, Ti and the descending is Ti, Te/Ta, La, Le/Lo, Sol, Se, Fa, Mi, Me/Ma, Re, Ra, Do, However, once 0 is given to a note, due to octave equivalence, the chromatic scale may be indicated unambiguously by the numbers 0-11 mod twelve. Thus two perfect fifths are 0-7-2. Tone rows, orderings used in the twelve-tone technique, are often considered this way due to the increased ease of comparing inverse intervals and forms (inversional equivalence).
Pitch-rational tunings
Pythagorean
The most common conception of the chromatic scale before the 13th century was the Pythagorean chromatic scale (ⓘ). Due to a different tuning technique, the twelve semitones in this scale have two slightly different sizes. Thus, the scale is not perfectly symmetric. Many other tuning systems, developed in the ensuing centuries, share a similar asymmetry.
In Pythagorean tuning (i.e. 3-limit just intonation) the chromatic scale is tuned as follows, in perfect fifths from G♭ to A♯ centered on D (in bold) (G♭–D♭–A♭–E♭–B♭–F–C–G–D–A–E–B–F♯–C♯–G♯–D♯–A♯), with sharps higher than their enharmonic flats (cents rounded to one decimal):
C D♭ C♯ D E♭ D♯ E F G♭ F♯ G A♭ G♯ A B♭ A♯ B C Pitch
ratio1 256⁄243 2187⁄2048 9⁄8 32⁄27 19683⁄16384 81⁄64 4⁄3 1024⁄729 729⁄512 3⁄2 128⁄81 6561⁄4096 27⁄16 16⁄9 59049⁄32768 243⁄128 2 Cents 0 90.2 113.7 203.9 294.1 317.6 407.8 498 588.3 611.7 702 792.2 815.6 905.9 996.1 1019.6 1109.8 1200
where 256⁄243 is a diatonic semitone (Pythagorean limma) and 2187⁄2048 is a chromatic semitone (Pythagorean apotome).
The chromatic scale in Pythagorean tuning can be tempered to the 17-EDO tuning (P5 = 10 steps = 705.88 cents).
Just intonation
In 5-limit just intonation the chromatic scale, Ptolemy's intense chromatic scale[citation needed], is as follows, with flats higher than their enharmonic sharps, and new notes between E–F and B–C (cents rounded to one decimal):
C C♯ D♭ D D♯ E♭ E E♯/F♭ F F♯ G♭ G G♯ A♭ A A♯ B♭ B B♯/C♭ C Pitch ratio 1 25⁄24 16⁄15 9⁄8 75⁄64 6⁄5 5⁄4 32⁄25 4⁄3 25⁄18 36⁄25 3⁄2 25⁄16 8⁄5 5⁄3 125⁄72 9⁄5 15⁄8 48⁄25 2 Cents 0 70.7 111.7 203.9 274.6 315.6 386.3 427.4 498 568.7 631.3 702 772.6 813.7 884.4 955 1017.6 1088.3 1129.3 1200
The fractions 9⁄8 and 10⁄9, 6⁄5 and 32⁄27, 5⁄4 and 81⁄64, 4⁄3 and 27⁄20, and many other pairs are interchangeable, as 81⁄80 (the syntonic comma) is tempered out.[clarification needed]
Just intonation tuning can be approximated by 19-EDO tuning (P5 = 11 steps = 694.74 cents).
Non-Western cultures
The ancient Chinese chromatic scale is called Shí-èr-lǜ. However, "it should not be imagined that this gamut ever functioned as a scale, and it is erroneous to refer to the 'Chinese chromatic scale', as some Western writers have done. The series of twelve notes known as the twelve lü were simply a series of fundamental notes from which scales could be constructed."[8] However, "from the standpoint of tonal music [the chromatic scale] is not an independent scale, but derives from the diatonic scale,"[2] making the Western chromatic scale a gamut of fundamental notes from which scales could be constructed as well.
See also
- Atonality
- Chromaticism
- Twelve-tone technique
- 20th century music#Classical
- "All Through the Night" (Cole Porter song)
Notes
- ^ As every chromatic scale is identical under transposition, inversion, and retrograde to every other.
Sources
- ^ Jeans, James (1923). Science and Music. Cambridge University Press. pp. 24–25 – via Internet Archive.
- ^ a b c Forte, Allen, Tonal Harmony, third edition (S.l.: Holt, Rinehart, and Wilson, 1979): pp. 4–5. ISBN 0-03-020756-8.
- ^ Piston, Walter (1987/1941). Harmony, p. 5. 5th ed. revised by DeVoto, Mark. W. W. Norton, New York/London. ISBN 0-393-95480-3.
- ^ a b Benward, Bruce; Saker, Marilyn Nadine (2003). Music in Theory and Practice. Vol. I (7th ed.). McGraw-Hill. p. 37. ISBN 978-0-07-294262-0.
- ^ Benward & Saker (2003). "Glossary", p. 359.
- ^ Kamien, Roger (1990). Music: An Appreciation, p. 44. Brief edition. McGraw-Hill. ISBN 0-07-033568-0.
- ^ McCartin, Brian J. (November 1998). "Prelude to Musical Geometry". The College Mathematics Journal. 29 (5): 354–370 (364). doi:10.1080/07468342.1998.11973971. JSTOR 2687250.
- ^ Needham, Joseph (1962/2004). Science and Civilization in China, Vol. IV: Physics and Physical Technology, pp. 170–171. ISBN 978-0-521-05802-5.
Further reading
- Hewitt, Michael. 2013. Musical Scales of the World. The Note Tree. ISBN 978-0957547001
External links
- The Chromatic Scale arranged for guitar in several fingerings. (Formatted for easy printing)
- The 12 golden notes of music
- Chromatic Scale – Analysis

![{\displaystyle {\sqrt[{12}]{2}}\approxeq 1.06}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1241dd2aeab3b8ebf705cfe7d1ca86f0c07d905b)

