The twelve-tone technique—also known as dodecaphony, twelve-tone serialism, and (in British usage) twelve-note composition—is a method of musical composition first devised by Austrian composer Josef Matthias Hauer,[not verified in body] who published his "law of the twelve tones" in 1919. In 1923, Arnold Schoenberg (1874–1951) developed his own, better-known version of 12-tone technique, which became associated with the "Second Viennese School" composers, who were the primary users of the technique in the first decades of its existence. The technique is a means of ensuring that all 12 notes of the chromatic scale are sounded as often as one another in a piece of music while preventing the emphasis of any one note[3] through the use of tone rows, orderings of the 12 pitch classes. All 12 notes are thus given more or less equal importance, and the music avoids being in a key. Over time, the technique increased greatly in popularity and eventually became widely influential on 20th-century composers. Many important composers who had originally not subscribed to or actively opposed the technique, such as Aaron Copland and Igor Stravinsky,[clarification needed] eventually adopted it in their music.
Schoenberg himself described the system as a "Method of composing with twelve tones which are related only with one another".[4] It is commonly considered a form of serialism.
Schoenberg's fellow countryman and contemporary Hauer also developed a similar system using unordered hexachords or tropes—but with no connection to Schoenberg's twelve-tone technique.[contradictory] Other composers have created systematic use of the chromatic scale, but Schoenberg's method is considered to be most historically and aesthetically significant.[5]
YouTube Encyclopedic
-
1/5Views:41 4246 11523 9711 19743 912
-
The Twelve Tone System in Context
-
4 Chords of 12-Tone Serialism (Girls Like You)
-
Musical Sudoku: Serialism's History and Techniques
-
12 Tone Music Part 1 of 4 (Introduction)
-
Music Theory: Introduction to Twelve-Tone Serialism
Transcription
History of use
Though most sources will say it was invented by Austrian composer Arnold Schoenberg in 1921 and first described privately to his associates in 1923, in fact Josef Matthias Hauer published his "law of the twelve tones" in 1919, requiring that all twelve chromatic notes sound before any note is repeated.[8][failed verification] The method was used during the next twenty years almost exclusively by the composers of the Second Viennese School—Alban Berg, Anton Webern, and Schoenberg himself.
The twelve tone technique was preceded by "freely" atonal pieces of 1908–1923 which, though "free", often have as an "integrative element ... a minute intervallic cell" which in addition to expansion may be transformed as with a tone row, and in which individual notes may "function as pivotal elements, to permit overlapping statements of a basic cell or the linking of two or more basic cells".[9] The twelve-tone technique was also preceded by "nondodecaphonic serial composition" used independently in the works of Alexander Scriabin, Igor Stravinsky, Béla Bartók, Carl Ruggles, and others.[10] Oliver Neighbour argues that Bartók was "the first composer to use a group of twelve notes consciously for a structural purpose", in 1908 with the third of his fourteen bagatelles.[11] "Essentially, Schoenberg and Hauer systematized and defined for their own dodecaphonic purposes a pervasive technical feature of 'modern' musical practice, the ostinato".[10] Additionally, John Covach argues that the strict distinction between the two, emphasized by authors including Perle, is overemphasized:
The distinction often made between Hauer and the Schoenberg school—that the former's music is based on unordered hexachords while the latter's is based on an ordered series—is false: while he did write pieces that could be thought of as "trope pieces", much of Hauer's twelve-tone music employs an ordered series.[12]
The "strict ordering" of the Second Viennese school, on the other hand, "was inevitably tempered by practical considerations: they worked on the basis of an interaction between ordered and unordered pitch collections."[13]
Rudolph Reti, an early proponent, says: "To replace one structural force (tonality) by another (increased thematic oneness) is indeed the fundamental idea behind the twelve-tone technique", arguing it arose out of Schoenberg's frustrations with free atonality,[14][page needed] providing a "positive premise" for atonality.[3] In Hauer's breakthrough piece Nomos, Op. 19 (1919) he used twelve-tone sections to mark out large formal divisions, such as with the opening five statements of the same twelve-tone series, stated in groups of five notes making twelve five-note phrases.[13]
Felix Khuner contrasted Hauer's more mathematical concept with Schoenberg's more musical approach.[15] Schoenberg's idea in developing the technique was for it to "replace those structural differentiations provided formerly by tonal harmonies".[4] As such, twelve-tone music is usually atonal, and treats each of the 12 semitones of the chromatic scale with equal importance, as opposed to earlier classical music which had treated some notes as more important than others (particularly the tonic and the dominant note).
The technique became widely used by the fifties, taken up by composers such as Milton Babbitt, Luciano Berio, Pierre Boulez, Luigi Dallapiccola, Ernst Krenek, Riccardo Malipiero, and, after Schoenberg's death, Igor Stravinsky. Some of these composers extended the technique to control aspects other than the pitches of notes (such as duration, method of attack and so on), thus producing serial music. Some even subjected all elements of music to the serial process.
Charles Wuorinen said in a 1962 interview that while "most of the Europeans say that they have 'gone beyond' and 'exhausted' the twelve-tone system", in America, "the twelve-tone system has been carefully studied and generalized into an edifice more impressive than any hitherto known."[16]
American composer Scott Bradley, best known for his musical scores for work like Tom & Jerry and Droopy Dog, utilized the 12-tone technique in his work. Bradley described his use thus:
The Twelve-Tone System provides the 'out-of-this-world' progressions so necessary to under-write the fantastic and incredible situations which present-day cartoons contain.[17]
An example of Bradley's use of the technique to convey building tension occurs in the Tom & Jerry short "Puttin' on the Dog", from 1944. In a scene where the mouse, wearing a dog mask, runs across a yard of dogs "in disguise", a chromatic scale represents both the mouse's movements, and the approach of a suspicious dog, mirrored octaves lower.[18] Apart from his work in cartoon scores, Bradley also composed tone poems that were performed in concert in California.[19]
Rock guitarist Ron Jarzombek used a twelve-tone system for composing Blotted Science's extended play The Animation of Entomology. He put the notes into a clock and rearranged them to be used that are side by side or consecutive He called his method "Twelve-Tone in Fragmented Rows."[20]
Tone row
The basis of the twelve-tone technique is the tone row, an ordered arrangement of the twelve notes of the chromatic scale (the twelve equal tempered pitch classes). There are four postulates or preconditions to the technique which apply to the row (also called a set or series), on which a work or section is based:[21]
- The row is a specific ordering of all twelve notes of the chromatic scale (without regard to octave placement).
- No note is repeated within the row.
- The row may be subjected to interval-preserving transformations—that is, it may appear in inversion (denoted I), retrograde (R), or retrograde-inversion (RI), in addition to its "original" or prime form (P).
- The row in any of its four transformations may begin on any degree of the chromatic scale; in other words it may be freely transposed. (Transposition being an interval-preserving transformation, this is technically covered already by 3.) Transpositions are indicated by an integer between 0 and 11 denoting the number of semitones: thus, if the original form of the row is denoted P0, then P1 denotes its transposition upward by one semitone (similarly I1 is an upward transposition of the inverted form, R1 of the retrograde form, and RI1 of the retrograde-inverted form).
(In Hauer's system postulate 3 does not apply.)[2]
A particular transformation (prime, inversion, retrograde, retrograde-inversion) together with a choice of transpositional level is referred to as a set form or row form. Every row thus has up to 48 different row forms. (Some rows have fewer due to symmetry; see the sections on derived rows and invariance below.)
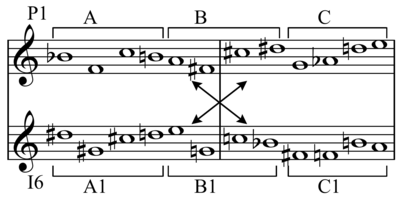
Example
Suppose the prime form of the row is as follows:
Then the retrograde is the prime form in reverse order:
The inversion is the prime form with the intervals inverted (so that a rising minor third becomes a falling minor third, or equivalently, a rising major sixth):
And the retrograde inversion is the inverted row in retrograde:
P, R, I and RI can each be started on any of the twelve notes of the chromatic scale, meaning that 47 permutations of the initial tone row can be used, giving a maximum of 48 possible tone rows. However, not all prime series will yield so many variations because transposed transformations may be identical to each other. This is known as invariance. A simple case is the ascending chromatic scale, the retrograde inversion of which is identical to the prime form, and the retrograde of which is identical to the inversion (thus, only 24 forms of this tone row are available).

In the above example, as is typical, the retrograde inversion contains three points where the sequence of two pitches are identical to the prime row. Thus the generative power of even the most basic transformations is both unpredictable and inevitable. Motivic development can be driven by such internal consistency.
Application in composition
Note that rules 1–4 above apply to the construction of the row itself, and not to the interpretation of the row in the composition. (Thus, for example, postulate 2 does not mean, contrary to common belief, that no note in a twelve-tone work can be repeated until all twelve have been sounded.) While a row may be expressed literally on the surface as thematic material, it need not be, and may instead govern the pitch structure of the work in more abstract ways. Even when the technique is applied in the most literal manner, with a piece consisting of a sequence of statements of row forms, these statements may appear consecutively, simultaneously, or may overlap, giving rise to harmony.

Durations, dynamics and other aspects of music other than the pitch can be freely chosen by the composer, and there are also no general rules about which tone rows should be used at which time (beyond their all being derived from the prime series, as already explained). However, individual composers have constructed more detailed systems in which matters such as these are also governed by systematic rules (see serialism).
Topography
Analyst Kathryn Bailey has used the term 'topography' to describe the particular way in which the notes of a row are disposed in her work on the dodecaphonic music of Webern. She identifies two types of topography in Webern's music: block topography and linear topography.
The former, which she views as the 'simplest', is defined as follows: 'rows are set one after the other, with all notes sounding in the order prescribed by this succession of rows, regardless of texture'. The latter is more complex: the musical texture 'is the product of several rows progressing simultaneously in as many voices' (note that these 'voices' are not necessarily restricted to individual instruments and therefore cut across the musical texture, operating as more of a background structure).[23]
Elisions, Chains, and Cycles
Serial rows can be connected through elision, a term that describes 'the overlapping of two rows that occur in succession, so that one or more notes at the juncture are shared (are played only once to serve both rows)'.[24] When this elision incorporates two or more notes it creates a row chain;[25] when multiple rows are connected by the same elision (typically identified as the same in set-class terms) this creates a row chain cycle, which therefore provides a technique for organising groups of rows.[26]
Properties of transformations
The tone row chosen as the basis of the piece is called the prime series (P). Untransposed, it is notated as P0. Given the twelve pitch classes of the chromatic scale, there are 12 factorial[27] (479,001,600[13]) tone rows, although this is far higher than the number of unique tone rows (after taking transformations into account). There are 9,985,920 classes of twelve-tone rows up to equivalence (where two rows are equivalent if one is a transformation of the other).[28]
Appearances of P can be transformed from the original in three basic ways:
- transposition up or down, giving Pχ.
- reversing the order of the pitches, giving the retrograde (R)
- turning each interval direction to its opposite, giving the inversion (I).
The various transformations can be combined. These give rise to a set-complex of forty-eight forms of the set, 12 transpositions of the four basic forms: P, R, I, RI. The combination of the retrograde and inversion transformations is known as the retrograde inversion (RI).
RI is: RI of P, R of I, and I of R. R is: R of P, RI of I, and I of RI. I is: I of P, RI of R, and R of RI. P is: R of R, I of I, and RI of RI.
thus, each cell in the following table lists the result of the transformations, a four-group, in its row and column headers:
P: RI: R: I: RI: P I R R: I P RI I: R RI P
However, there are only a few numbers by which one may multiply a row and still end up with twelve tones. (Multiplication is in any case not interval-preserving.)
Derivation
Derivation is transforming segments of the full chromatic, fewer than 12 pitch classes, to yield a complete set, most commonly using trichords, tetrachords, and hexachords. A derived set can be generated by choosing appropriate transformations of any trichord except 0,3,6, the diminished triad[citation needed]. A derived set can also be generated from any tetrachord that excludes the interval class 4, a major third, between any two elements. The opposite, partitioning, uses methods to create segments from sets, most often through registral difference.
Combinatoriality
Combinatoriality is a side-effect of derived rows where combining different segments or sets such that the pitch class content of the result fulfills certain criteria, usually the combination of hexachords which complete the full chromatic.
Invariance
Invariant formations are also the side effect of derived rows where a segment of a set remains similar or the same under transformation. These may be used as "pivots" between set forms, sometimes used by Anton Webern and Arnold Schoenberg.[30]
Invariance is defined as the "properties of a set that are preserved under [any given] operation, as well as those relationships between a set and the so-operationally transformed set that inhere in the operation",[31] a definition very close to that of mathematical invariance. George Perle describes their use as "pivots" or non-tonal ways of emphasizing certain pitches. Invariant rows are also combinatorial and derived.
Cross partition

A cross partition is an often monophonic or homophonic technique which, "arranges the pitch classes of an aggregate (or a row) into a rectangular design", in which the vertical columns (harmonies) of the rectangle are derived from the adjacent segments of the row and the horizontal columns (melodies) are not (and thus may contain non-adjacencies).[33]
For example, the layout of all possible 'even' cross partitions is as follows:[34]
62 43 34 26 ** *** **** ****** ** *** **** ****** ** *** **** ** *** ** **
One possible realization out of many for the order numbers of the 34 cross partition, and one variation of that, are:[34]
0 3 6 9 0 5 6 e 1 4 7 t 2 3 7 t 2 5 8 e 1 4 8 9
Thus if one's tone row was 0 e 7 4 2 9 3 8 t 1 5 6, one's cross partitions from above would be:
0 4 3 1 0 9 3 6 e 2 8 5 7 4 8 5 7 9 t 6 e 2 t 1
Cross partitions are used in Schoenberg's Op. 33a Klavierstück and also by Berg but Dallapicolla used them more than any other composer.[35]
Other
In practice, the "rules" of twelve-tone technique have been bent and broken many times, not least by Schoenberg himself. For instance, in some pieces two or more tone rows may be heard progressing at once, or there may be parts of a composition which are written freely, without recourse to the twelve-tone technique at all. Offshoots or variations may produce music in which:
- the full chromatic is used and constantly circulates, but permutational devices are ignored
- permutational devices are used but not on the full chromatic
Also, some composers, including Stravinsky, have used cyclic permutation, or rotation, where the row is taken in order but using a different starting note. Stravinsky also preferred the inverse-retrograde, rather than the retrograde-inverse, treating the former as the compositionally predominant, "untransposed" form.[36]
Although usually atonal, twelve tone music need not be—several pieces by Berg, for instance, have tonal elements.
One of the best known twelve-note compositions is Variations for Orchestra by Arnold Schoenberg. "Quiet", in Leonard Bernstein's Candide, satirizes the method by using it for a song about boredom, and Benjamin Britten used a twelve-tone row—a "tema seriale con fuga"—in his Cantata Academica: Carmen Basiliense (1959) as an emblem of academicism.[37]
Schoenberg's mature practice
Ten features of Schoenberg's mature twelve-tone practice are characteristic, interdependent, and interactive:[38]
- Hexachordal inversional combinatoriality
- Aggregates
- Linear set presentation
- Partitioning
- Isomorphic partitioning
- Invariants
- Hexachordal levels
- Harmony, "consistent with and derived from the properties of the referential set"
- Metre, established through "pitch-relational characteristics"
- Multidimensional set presentations.
See also
- List of dodecaphonic and serial compositions
- All-interval twelve-tone row
- All-interval tetrachord
- All-trichord hexachord
- Pitch interval
- List of tone rows and series
References
Notes
- ^ Whittall 2008, 26.
- ^ a b Perle 1991, 145.
- ^ a b Perle 1977, 2.
- ^ a b Schoenberg 1975, 218.
- ^ Whittall 2008, 25.
- ^ Leeuw 2005, 149.
- ^ Leeuw 2005, 155–157.
- ^ Schoenberg 1975, 213.
- ^ Perle 1977, 9–10.
- ^ a b Perle 1977, 37.
- ^ Neighbour 1955, 53.
- ^ John Covach quoted in Whittall 2008, 24.
- ^ a b c Whittall 2008, 24.
- ^ Reti 1958
- ^ Crawford and Khuner 1996, 28.
- ^ Chase 1987, 587.
- ^ Yowp (7 January 2017). "Tralfaz: Cartoon Composer Scott Bradley".
- ^ Goldmark, Daniel (2007). Tunes for 'Toons: Music and the Hollywood Cartoon. Univ of California Press. p. 71. ISBN 978-0-520-25311-7.
- ^ Scott Bradley at IMDb
- ^ Mustein, Dave (2 November 2011). "Blotted Science's Ron Jarzombek: The Twelve-tone Metalsucks Interview". MetalSucks. Retrieved 19 January 2021.
- ^ Perle 1977, 3.
- ^ Whittall 2008, 52.
- ^ Bailey, Kathryn (2006). The twelve-note music of Anton Webern: old forms in a new language. Music in the twentieth century (Digitally printed 1st pbk. version ed.). Cambridge [England] New York: Cambridge University Press. p. 31. ISBN 978-0-521-39088-0.
- ^ Bailey, Kathryn (2006). The twelve-note music of Anton Webern: old forms in a new language. Music in the twentieth century (Digitally printed 1st pbk. version ed.). Cambridge [England] New York: Cambridge University Press. p. 449. ISBN 978-0-521-39088-0.
- ^ Moseley, Brian (1 September 2019). "Transformation Chains, Associative Areas, and a Principle of Form for Anton Webern's Twelve-tone Music". Music Theory Spectrum. 41 (2): 218–243. doi:10.1093/mts/mtz010. ISSN 0195-6167.
- ^ Moseley, Brian (2018). "Cycles in Webern's Late Music". Journal of Music Theory. 62 (2): 165–204. doi:10.1215/00222909-7127658. ISSN 0022-2909. S2CID 171497028.
- ^ Loy 2007, 310.
- ^ Benson 2007, 348.
- ^ Haimo 1990, 27.
- ^ Perle 1977, 91–93.
- ^ Babbitt 1960, 249–250.
- ^ Haimo 1990, 13.
- ^ Alegant 2010, 20.
- ^ a b Alegant 2010, 21.
- ^ Alegant 2010, 22, 24.
- ^ Spies 1965, 118.
- ^ Brett 2007.
- ^ Haimo 1990, 41.
Sources
- Alegant, Brian. 2010. The Twelve-Tone Music of Luigi Dallapiccola. Eastman Studies in Music 76. Rochester, New York: University of Rochester Press. ISBN 978-1-58046-325-6.
- Babbitt, Milton. 1960. "Twelve-Tone Invariants as Compositional Determinants". The Musical Quarterly 46, no. 2, Special Issue: Problems of Modern Music: The Princeton Seminar in Advanced Musical Studies (April): 246–259. doi:10.1093/mq/XLVI.2.246. JSTOR 740374(subscription required).
- Babbitt, Milton. 1961. "Set Structure as a Compositional Determinant". Journal of Music Theory 5, no. 1 (Spring): 72–94. JSTOR 842871(subscription required).
- Benson, Dave. 2007 Music: A Mathematical Offering. Cambridge and New York: Cambridge University Press. ISBN 978-0-521-85387-3.
- Brett, Philip. "Britten, Benjamin." Grove Music Online ed. L. Macy (Accessed 8 January 2007)
- Chase, Gilbert. 1987. America's Music: From the Pilgrims to the Present, revised third edition. Music in American Life. Urbana: University of Illinois Press. ISBN 0-252-00454-X (cloth); ISBN 0-252-06275-2 (pbk).
- Crawford, Caroline and Felix Khuner. 1996. Felix Khuner: A Violinist's Journey from Vienna's Kolisch Quartet to the San Francisco Symphony and Opera Orchestras, intro. by Tom Heimberg. Regional Oral History Office, The Bancroft Library. Berkeley: University of California.
- Haimo, Ethan. 1990. Schoenberg's Serial Odyssey: The Evolution of his Twelve-Tone Method, 1914–1928. Oxford [England] Clarendon Press; New York: Oxford University Press ISBN 0-19-315260-6.
- Hill, Richard S. 1936. "Schoenberg's Tone-Rows and the Tonal System of the Future". The Musical Quarterly 22, no. 1 (January): 14–37. doi:10.1093/mq/XXII.1.14. JSTOR 739013(subscription required).
- Lansky, Paul; George Perle and Dave Headlam. 2001. "Twelve-note Composition". The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan.
- Leeuw, Ton de. 2005. Music of the Twentieth Century: A Study of Its Elements and Structure, translated from the Dutch by Stephen Taylor. Amsterdam: Amsterdam University Press. ISBN 90-5356-765-8. Translation of Muziek van de twintigste eeuw: een onderzoek naar haar elementen en structuur. Utrecht: Oosthoek, 1964. Third impression, Utrecht: Bohn, Scheltema & Holkema, 1977. ISBN 90-313-0244-9.
- Loy, D. Gareth, 2007. Musimathics: The Mathematical Foundations of Music, Vol. 1. Cambridge, Massachusetts and London: MIT Press. ISBN 978-0-262-12282-5.
- Neighbour, Oliver. 1954. "The Evolution of Twelve-Note Music". Proceedings of the Royal Musical Association, volume 81, issue 1: 49–61. doi:10.1093/jrma/81.1.49
- Perle, George. 1977. Serial Composition and Atonality: An Introduction to the Music of Schoenberg, Berg, and Webern, fourth edition, revised. Berkeley, Los Angeles, and London: University of California Press. ISBN 0-520-03395-7
- Perle, George. 1991. Serial Composition and Atonality: An Introduction to the Music of Schoenberg, Berg, and Webern, sixth edition, revised. Berkeley: University of California Press. ISBN 978-0-520-07430-9.
- Reti, Rudolph. 1958. Tonality, Atonality, Pantonality: A Study of Some Trends in Twentieth Century Music. Westport, Connecticut: Greenwood Press. ISBN 0-313-20478-0.
- Rufer, Josef. 1954. Composition with Twelve Notes Related Only to One Another, translated by Humphrey Searle. New York: The Macmillan Company. (Original German ed., 1952)
- Schoenberg, Arnold. 1975. Style and Idea, edited by Leonard Stein with translations by Leo Black. Berkeley & Los Angeles: University of California Press. ISBN 0-520-05294-3.
- 207–208 "Twelve-Tone Composition (1923)"
- 214–245 "Composition with Twelve Tones (1) (1941)"
- 245–249 "Composition with Twelve Tones (2) (c. 1948)"
- Solomon, Larry. 1973. "New Symmetric Transformations". Perspectives of New Music 11, no. 2 (Spring–Summer): 257–264. JSTOR 832323(subscription required).
- Spies, Claudio. 1965. "Notes on Stravinsky's Abraham and Isaac". Perspectives of New Music 3, no. 2 (Spring–Summer): 104–126. JSTOR 832508(subscription required).
- Whittall, Arnold. 2008. The Cambridge Introduction to Serialism. Cambridge Introductions to Music. New York: Cambridge University Press. ISBN 978-0-521-86341-4 (cloth) ISBN 978-0-521-68200-8 (pbk).
Further reading
- Covach, John. 1992. "The Zwölftonspiel of Josef Matthias Hauer". Journal of Music Theory 36, no. 1 (Spring): 149–84. JSTOR 843913(subscription required).
- Covach, John. 2000. "Schoenberg's 'Poetics of Music', the Twelve-tone Method, and the Musical Idea". In Schoenberg and Words: The Modernist Years, edited by Russell A. Berman and Charlotte M. Cross, New York: Garland. ISBN 0-8153-2830-3
- Covach, John. 2002, "Twelve-tone Theory". In The Cambridge History of Western Music Theory, edited by Thomas Christensen, 603–627. Cambridge: Cambridge University Press. ISBN 0-521-62371-5.
- Krenek, Ernst. 1953. "Is the Twelve-Tone Technique on the Decline?" The Musical Quarterly 39, no 4 (October): 513–527.
- Šedivý, Dominik. 2011. Serial Composition and Tonality. An Introduction to the Music of Hauer and Steinbauer, edited by Günther Friesinger, Helmut Neumann and Dominik Šedivý. Vienna: edition mono. ISBN 3-902796-03-0
- Sloan, Susan L. 1989. "Archival Exhibit: Schoenberg's Dodecaphonic Devices". Journal of the Arnold Schoenberg Institute 12, no. 2 (November): 202–205.
- Starr, Daniel. 1978. "Sets, Invariance and Partitions". Journal of Music Theory 22, no. 1 (Spring): 1–42. JSTOR 843626(subscription required).
- Wuorinen, Charles. 1979. Simple Composition. New York: Longman. ISBN 0-582-28059-1. Reprinted 1991, New York: C. F. Peters. ISBN 0-938856-06-5.
External links
- Twelve tone square to find all combinations of a 12 tone sequence
- New Transformations: Beyond P, I, R, and RI by Larry Solomon
- Javascript twelve tone matrix calculator and tone row analyzer
- Matrix generator from musictheory.net by Ricci Adams
- Twelve-Tone Technique, A Quick Reference by Dan Román
- Twelve Tones by mathemusician Vi Hart on YouTube
- Dodecaphonic Knots and Topology of Words by Franck Jedrzejewski
- Database on tone rows and tropes