| Type | Syllogism |
|---|---|
| Field |
|
| Statement | Whenever instances of , and appear on lines of a proof, can be placed on a subsequent line. |
| Symbolic statement |
In classical logic, a hypothetical syllogism is a valid argument form, a deductive syllogism with a conditional statement for one or both of its premises. Ancient references point to the works of Theophrastus and Eudemus for the first investigation of this kind of syllogisms.[1][2]
YouTube Encyclopedic
-
1/5Views:45 98919 48734 9552 691573 984
-
Hypothetical Syllogism
-
Hypothetical Syllogism
-
Logic 101 (#30): Hypothetical Syllogism
-
Hypothetical Syllogism and Disjunctive Syllogism | Rules of Inference of Propositional logic |
-
RULES of INFERENCE - DISCRETE MATHEMATICS
Transcription
Types
Hypothetical syllogisms come in two types: mixed and pure. A mixed hypothetical syllogism has two premises: one conditional statement and one statement that either affirms or denies the antecedent or consequent of that conditional statement. For example,
- If P, then Q.
- P.
- ∴ Q.
In this example, the first premise is a conditional statement in which "P" is the antecedent and "Q" is the consequent. The second premise "affirms" the antecedent. The conclusion, that the consequent must be true, is deductively valid.
A mixed hypothetical syllogism has four possible forms, two of which are valid, while the other two are invalid. A valid mixed hypothetical syllogism either affirms the antecedent (modus ponens) or denies the consequent (modus tollens).[3] An invalid hypothetical syllogism either affirms the consequent (fallacy of the converse) or denies the antecedent (fallacy of the inverse).
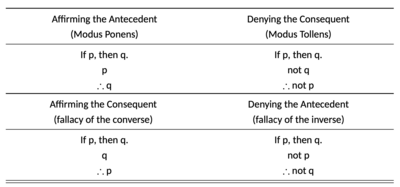
A pure hypothetical syllogism is a syllogism in which both premises and the conclusion are all conditional statements. The antecedent of one premise must match the consequent of the other for the conditional to be valid. Consequently, conditionals contain remained antecedent as antecedent and remained consequent as consequent.
- If P, then Q.
- If Q, then R.
- ∴ If P, then R.
An example in English:
- If I do not wake up, then I cannot go to work.
- If I cannot go to work, then I will not get paid.
- Therefore, if I do not wake up, then I will not get paid.
Propositional logic
In propositional logic, hypothetical syllogism is the name of a valid rule of inference (often abbreviated HS and sometimes also called the chain argument, chain rule, or the principle of transitivity of implication). The rule may be stated:
In other words, whenever instances of "", and "" appear on lines of a proof, "" can be placed on a subsequent line.
Applicability
The rule of hypothetical syllogism holds in classical logic, intuitionistic logic, most systems of relevance logic, and many other systems of logic. However, it does not hold in all logics, including, for example, non-monotonic logic, probabilistic logic and default logic. The reason for this is that these logics describe defeasible reasoning, and conditionals that appear in real-world contexts typically allow for exceptions, default assumptions, ceteris paribus conditions, or just simple uncertainty.
An example, derived from Ernest W. Adams, [4]
- If Jones wins the election, Smith will retire after the election.
- If Smith dies before the election, Jones will win the election.
- If Smith dies before the election, Smith will retire after the election.
Clearly, (3) does not follow from (1) and (2). (1) is true by default, but fails to hold in the exceptional circumstances of Smith dying. In practice, real-world conditionals always tend to involve default assumptions or contexts, and it may be infeasible or even impossible to specify all the exceptional circumstances in which they might fail to be true. For similar reasons, the rule of hypothetical syllogism does not hold for counterfactual conditionals.
Formal notation
The hypothetical syllogism inference rule may be written in sequent notation, which amounts to a specialization of the cut rule:
where is a metalogical symbol and meaning that is a syntactic consequence of in some logical system;
and expressed as a truth-functional tautology or theorem of propositional logic:
where , , and are propositions expressed in some formal system.
Proof
| Step | Proposition | Derivation |
|---|---|---|
| 1 | Given | |
| 2 | Given | |
| 3 | Conditional proof assumption | |
| 4 | Modus ponens (1,3) | |
| 5 | Modus ponens (2,4) | |
| 6 | Conditional Proof (3-5) |
Alternative forms
An alternative form of hypothetical syllogism, more useful for classical propositional calculus systems with implication and negation (i.e. without the conjunction symbol), is the following:
- (HS1)
Yet another form is:
- (HS2)
Proof
An example of the proofs of these theorems in such systems is given below. We use two of the three axioms used in one of the popular systems described by Jan Łukasiewicz. The proofs relies on two out of the three axioms of this system:
- (A1)
- (A2)
The proof of the (HS1) is as follows:
- (1) (instance of (A1))
- (2) (instance of (A2))
- (3) (from (1) and (2) by modus ponens)
- (4) (instance of (A2))
- (5) (from (3) and (4) by modus ponens)
- (6) (instance of (A1))
- (7) (from (5) and (6) by modus ponens)
The proof of the (HS2) is given here.
As a metatheorem
Whenever we have two theorems of the form and , we can prove by the following steps:
- (1) (instance of the theorem proved above)
- (2) (instance of (T1))
- (3) (from (1) and (2) by modus ponens)
- (4) (instance of (T2))
- (5) (from (3) and (4) by modus ponens)
See also
- Plausible reasoning
- Transitive relation
- Type of syllogism (disjunctive, hypothetical, legal, poly-, prosleptic, quasi-, statistical)
References
- ^ "History of Logic: Theophrastus of Eresus" in Encyclopædia Britannica Online.
- ^ Susanne Bobzien,"The Development of Modus Ponens in Antiquity: "From Aristotle to the 2nd Century AD", Phronesis, Vol. 47, No. 4 (2002), pp. 359-394.
- ^ a b Kashef, Arman. (2023), In Quest of Univeral Logic: A brief overview of formal logic's evolution, doi:10.13140/RG.2.2.24043.82724/1
- ^ Adams, Ernest W. (1975). The Logic of Conditionals. Dordrecht: Reidel. p. 22.





























