Корона (теория графов)

В теории графов короной с 2n вершинами называется неориентированный граф с двумя наборами вершин u_i и v_i и рёбрами между u_i и v_j, если i ≠ j. Можно рассматривать корону как полный двудольный граф, из которого удалено совершенное паросочетание, как двойное покрытие двудольным графом полного графа, или как двудольный граф Кнезера H_n,1, представляющий подмножества из 1 элемента и (n − 1) элементов множества из n элементов с рёбрами между двумя подмножествами, если одно подмножество содержится в другом.

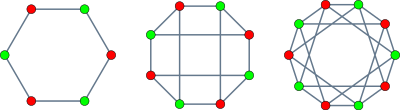
Примеры

Корона с шестью вершинами образует цикл, а корона с восемью вершинами изоморфна графу куба. В двойной шестёрке Шлефли конфигурации 12 прямых и 30 точек в трёхмерном пространстве, двенадцать прямых пересекают друг друга по схеме короны с 12 вершинами.

Свойства

Число рёбер в короне является прямоугольным числом n(n − 1). Её ахроматическое число равно n — можно найти полную раскраску путём выбора пары {u_i, v_i} в качестве классов цвета^[1]. Короны являются симметричными и дистанционно-транзитивными графами. Архдьякон с соавторами^[2] описывают разбиение рёбер короны на циклы равной длины.

Корону с 2n вершинами можно вложить в четырёхмерное евклидово пространство так, что все её рёбра будут иметь длину единица. Однако такое вложение может поместить несмежные вершины на расстояние единица. Вложение, при котором рёбра имеют длину единица, а расстояние между любыми несмежными вершинами не равно единице, требует как минимум размерности n − 2. Это показывает, что для представления графа в виде графа единичных расстояний и графа строго единичных расстояний требуются совсем различные размерности^[3]. Минимальное число полных двудольных подграфов, требующихся для покрытия рёбер короны (её двудольная размерность, или размер минимального покрытия кликами) равно

${\displaystyle \sigma (n)=\min \left\{\,k\mid n\leq {\binom {k}{\lfloor k/2\rfloor }}\,\right\},}$

то есть обратная функция центрального биномиального коэффициента^[4].

Дополнением короны с 2n вершинами является прямое произведением полных графов K₂ ${\displaystyle \square }$ K_n, что эквивалентно ладейному графу 2 × n.

Приложение

В этикете — традиционных правилах рассаживания гостей за обеденным столом — мужчины и женщины должны перемежаться и ни одна семейная пара не должна сидеть рядом. Рассаживание, удовлетворяющее этим правилам для вечеринки n семейных пар, можно описать как гамильтонов цикл короны. Задача подсчёта числа возможных рассаживаний или, что почти то же самое^[5], что число гамильтоновых циклов в короне известна в комбинаторике как задача о гостях. Для корон с числом вершин 6, 8, 10, … число (ориентированных) гамильтоновых циклов равно

2, 12, 312, 9600, 416880, 23879520, 1749363840, … последовательность A094047 в OEIS.

Короны можно использовать, чтобы показать, что алгоритм жадной раскраски ведёт себя плохо в некоторых случаях — если вершины короны представлены алгоритму в порядке u₀, v₀, u₁, v₁, и т. д., то жадная раскраска использует n цветов, хотя оптимальным числом цветов является два. Это построение приписывается Джонсону^[6], а сами короны иногда называют графами Джонсона с обозначением J_n^[7]. Фюрер^[8] использовал короны как часть построения, показывающего сложность аппроксимации задачи раскраски.

Матушек^[9]использовал расстояние в коронах как пример метрического пространства, которое трудно вложить в нормированное векторное пространство.

Как показали Миклавич и Порошник^[10], короны входят в небольшое число различных типов графов, которые являются дистанционно-регулярными циркулянтными графами.

Агарвал и соавторы^[11] описывают многоугольники, имеющие короны в качестве графов видимости. Они используют их в качестве примера, чтобы показать, что представление графов в виде объединения полных двудольных графов не всегда эффективно по памяти.

Корона с 2n вершинами с рёбрами, ориентированными от одной стороны двудольного графа к другой, образует стандартный пример частично упорядоченного множества с размерностью упорядочения^[en] n.

Примечания

Ссылки

• Weisstein, Eric W. Crown Graph (англ.) на сайте Wolfram MathWorld.

Эта страница в последний раз была отредактирована 24 февраля 2023 в 22:14.