Расслоённое произведение (послойное произведение, коамальгама, декартов квадрат, англ. pullback) — теоретико-категорное понятие, определяемое как предел диаграммы, состоящей из двух морфизмов: Расслоённое произведение часто обозначают как
Двойственное понятие — кодекартов квадрат.
Универсальное свойство
Пусть в категории дана пара морфизмов и Расслоённое произведение и над — это объект вместе с морфизмами для которых следующая диаграмма коммутативна:
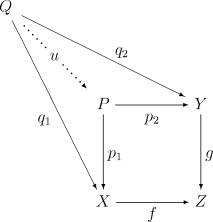
Более того, расслоённое произведение должно быть универсальным объектом с таким свойством: для любого объекта с парой морфизмов дополняющих пару до коммутативного квадрата, существует единственный морфизм такой что нижеприведённая диаграмма коммутативна:
Внутренний квадрат этой диаграммы, образованный морфизмами называется декартовым (или коуниверсальным) квадратом для пары морфизмов и
Как и другие объекты, определённые с помощью универсального свойства, расслоённое произведение не обязательно существует, но если существует, то определено с точностью до изоморфизма.
Примеры
В категории множеств расслоённое произведение множеств и с отображениями и — это множество
вместе с естественными проекциями на компоненты.
Аналогичным образом определяется расслоённое произведение в категории коммутативных колец.
Также расслоённое произведение в можно описывать двумя асимметричными способами:
где — дизъюнктное объединение множеств.
См. также
Литература
- Голдблатт Р. Топосы. Категорный анализ логики = Topoi. The categorial analysis of logic / Пер. с англ. В. Н. Гришина и В. В. Шокурова под ред. Д. А. Бочвара. — М.: Мир, 1983. — 488 с.
- Городенцев А. Л. Алгебра для студентов-математиков. Часть II. — М., 2015. — С. 160.
- Маклейн С. Глава 3. Универсальные конструкции и пределы // Категории для работающего математика = Categories for the working mathematician / Пер. с англ. под ред. В. А. Артамонова. — М.: Физматлит, 2004. — С. 68—94. — 352 с. — ISBN 5-9221-0400-4.
- Фейс К. Алгебра — кольца, модули и категории, том 1. — М.: Мир — том 190 серии Springer-Verlag — Grundlehren der mathematischen wissenschaften — 1977 [1973].
- Jiří Adámek, Horst Herrlich, George E. Strecker. Abstract and Concrete Categories. The Joy of Cats. — Willey & Sons, 1990. — P. 524. — ISBN 0-471-60922-6.
Обычно почти сразу, изредка в течении часа.























![{\displaystyle \cong \coprod _{x\in X}g^{-1}[\{f(x)\}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac3befa2469804444f4638bf0e0e06455a45d40d)
![{\displaystyle \cong \coprod _{y\in Y}f^{-1}[\{g(y)\}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe17b3e15afca43943e8e654e3793a13b7972e08)
