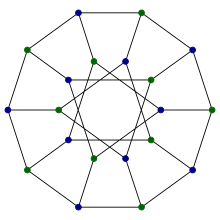
Граф Дезарга

Граф Дезарга
Назван в честь	Жерара Дезарга
Вершин	20
Рёбер	30
Радиус	5
Диаметр	5
Обхват	6
Автоморфизмы	240 (S5 × Z/2Z)
Хроматическое число	2
Хроматический индекс	3
Род	2
Свойства	кубический дистанционно-регулярный гамильтонов двудольный симметричный
Медиафайлы на Викискладе

Граф Дезарга — дистанционно-транзитивный кубический граф с 20 вершинами и 30 рёбрами^[1]. Назван в честь Жерара Дезарга. Возникает в некоторых комбинаторных построениях, имеет высокую степень симметрии, это единственный известный непланарный кубический частичный куб и применяется в химических базах данных.

Имя «граф Дезарга» употребляется также для графа с десятью вершинами, дополнения графа Петерсена, который можно получить как половина^[en] графа Дезарга с 20 вершинами.^[2]

Построение

Существует несколько различных путей построения графа Дезарга:

• Он является обобщённым графом Петерсена G(10, 3). Для получения графа Дезарга этим способом соединяем десять вершин в правильный десятиугольник и соединяем оставшиеся десять вершин в звезду с десятью вершинами, соединяя пары вершин на расстоянии три. Граф Дезарга состоит из 20 рёбер этих двух многоугольников вместе с дополнительными 10 рёбрами, соединяющими точки одного десятиугольника с соответствующими точками другого.
• Он является графом Леви конфигурации Дезарга. Эта конфигурация состоит из десяти точек и десяти прямых, образующих перспективу двух треугольников, их центр перспективы и их ось перспективы. Граф Дезарга имеет по вершине для каждой точки, по вершине для каждой прямой, и по одному ребру для каждой пары точка-прямая, если точка лежит на этой прямой. Теорема Дезарга, названная в честь французского математика 17-го века Жерара Дезарга, описывает множество точек и прямых, образующих эту конфигурацию. Конфигурация и граф получили своё название по этой теореме.
• Он является двойным двудольным покрытием графа Петерсена и образуется путём замены каждой вершины графа Петерсена парой вершин и каждого ребра графа Петерсена парой пересекающихся рёбер.
• Он является двудольным графом Кнезера H_5,2. Его вершины можно пометить десятью двухэлементными подмножествами и десятью трёхэлементными подмножествами пятиэлементного множества. В этой разметке ребро соединяет вершины, если одно из соответствующих множеств содержится в другом.
• Граф Дезарга является гамильтоновым и может быть построен по LCF-нотации: [5,−5,9,−9]⁵.

Алгебраические свойства

Граф Дезарга является симметричным графом — он имеет симметрии, которые переводят любую вершину в любую другую вершину и любое ребро в любое другое ребро. Его группа симметрии имеет порядок 240 и изоморфна произведению симметрических групп с 5 вершинами на группу порядка 2.

Можно представить это произведение симметрических групп в терминах построения графа Дезарга — симметрическая группа с 5 точками является группой симметрии конфигурации Дезарга, а подгруппа второго порядка обменивает роли вершин, которые представляют конфигурацию Дезарга и вершин, которые представляют прямые. Альтернативно, в терминах двудольного графа Кнесера, симметрическая группа с пятью точками действует раздельно на двухэлементном и трёхэлементном подмножествах пяти точек, и дополнение подмножеств образует группу порядка два, которая преобразует один тип подмножеств в другой. Симметрическая группа из пяти точек является также группой симметрии графа Петерсена, а подгруппа порядка 2 обменивает вершины в каждой паре вершин, образованных при двойном покрытии.

Обобщённый граф Петерсона G(n, k) является вершинно-транзитивным тогда и только тогда, когда n = 10 и k = 2 или если k² ≡ ±1 (mod n) и является рёберно-транзитивным только в семи следующих случаях: (n, k) = (4, 1), (5, 2), (8, 3), (10, 2), (10, 3), (12, 5), (24, 5).^[3] Таким образом, граф Дезарга — один из семи симметричных обобщённых графов Петерсена. В эти семь графов входят кубовой граф G(4, 1), граф Петерсена G(5, 2), граф Мёбиуса-Кантора G(8, 3), граф додекаэдра G(10, 2) и граф Науру G(12, 5).

Характеристический многочлен графа Дезарга равен

${\displaystyle (x-3)(x-2)^{4}(x-1)^{5}(x+1)^{5}(x+2)^{4}(x+3).}$

Таким образом, граф Дезарга является целочисленным графом — его спектр состоит полностью из целых чисел.

Приложения

В химии граф Дезарга известен как граф Дезарга — Леви. Он используется для построения системы стереоизомеров пенталигандов. В этом приложении тридцати рёбрам графа соответствуют псевдовращения^[en] лиганд.^[4][5]

Другие свойства

Граф Дезарга имеет число прямолинейных пересечений 6, и является наименьшим кубическим графом с таким числом пересечений (последовательность A110507 в OEIS). Он является единственным известным непланарным кубическим частичным кубом.^[6]

Граф Дезарга имеет хроматическое число 2, хроматический индекс 3, радиус 5, диаметр 5 и обхват 6. Он также является 3-вершинно-связным и рёберно 3-связным гамильтоновым графом.

Все кубические дистанционно-регулярные графы известны.^[7] Граф Дезарга — один из этих графов.

Галерея

• 
  Граф Дезарга, раскрашенный таким образом, чтобы выделить различные циклы.
• 
  Хроматический индекс графа Дезарга равен 3.
• 
  Хроматическое число графа Дезарга равно 2.

Примечания

Эта страница в последний раз была отредактирована 6 февраля 2021 в 21:06.