Snub square antiprism

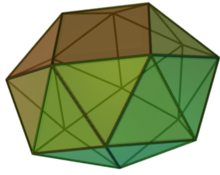
In geometry, the snub square antiprism is the Johnson solid that can be constructed by snubbing the square antiprism. It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids, although it is a relative of the icosahedron that has fourfold symmetry instead of threefold.

Construction and properties

The snub is the process of constructing polyhedra by cutting loose the edge's faces, twisting them, and then attaching equilateral triangles to their edges.^[1] As the name suggested, the snub square antiprism is constructed by snubbing the square antiprism,^[2] and this construction results in 24 equilateral triangles and 2 squares as its faces.^[3] The Johnson solids are the convex polyhedra whose faces are regular, and the snub square antiprism is one of them, enumerated as ${\displaystyle J_{85}}$, the 85th Johnson solid.^[4]

Let ${\displaystyle k\approx 0.82354}$ be the positive root of the cubic polynomial

Furthermore, let ${\displaystyle h\approx 1.35374}$ be defined by Then, Cartesian coordinates of a snub square antiprism with edge length 2 are given by the union of the orbits of the points under the action of the group generated by a rotation around the ${\displaystyle z}$-axis by 90° and by a rotation by 180° around a straight line perpendicular to the ${\displaystyle z}$-axis and making an angle of 22.5° with the ${\displaystyle x}$-axis.^[5] It has the three-dimensional symmetry of dihedral group ${\displaystyle D_{4h}}$ of order 8.^[2]

The surface area and volume of a snub square antiprism with edge length ${\displaystyle a}$ can be calculated as:^[3]

References

External links

• Weisstein, Eric W., "Snub square antiprism" ("Johnson solid") at MathWorld.