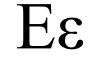 | ||||||||||||||||||||||||||||||||||||||||||||||||
| Greek alphabet | ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||||||||||||||||||||||||
| History | ||||||||||||||||||||||||||||||||||||||||||||||||
| Use in other languages | ||||||||||||||||||||||||||||||||||||||||||||||||
| Related topics | ||||||||||||||||||||||||||||||||||||||||||||||||
Epsilon (US: /ˈɛpsɪlɒn/,[1] UK: /ɛpˈsaɪlən/;[2] uppercase Ε, lowercase ε or ϵ; Greek: έψιλον) is the fifth letter of the Greek alphabet, corresponding phonetically to a mid front unrounded vowel IPA: [e̞] or IPA: [ɛ̝]. In the system of Greek numerals it also has the value five. It was derived from the Phoenician letter He ![]() . Letters that arose from epsilon include the Roman E, Ë and Ɛ, and Cyrillic Е, È, Ё, Є and Э.
. Letters that arose from epsilon include the Roman E, Ë and Ɛ, and Cyrillic Е, È, Ё, Є and Э.
The name of the letter was originally εἶ (Ancient Greek: [êː]), but it was later changed to ἒ ψιλόν (e psilon 'simple e') in the Middle Ages to distinguish the letter from the digraph αι, a former diphthong that had come to be pronounced the same as epsilon.
The uppercase form of epsilon is identical to Latin ⟨E⟩ but has its own code point in Unicode: U+0395 Ε GREEK CAPITAL LETTER EPSILON. The lowercase version has two typographical variants, both inherited from medieval Greek handwriting. One, the most common in modern typography and inherited from medieval minuscule, looks like a reversed number "3" and is encoded U+03B5 ε GREEK SMALL LETTER EPSILON. The other, also known as lunate or uncial epsilon and inherited from earlier uncial writing,[3][4] looks like a semicircle crossed by a horizontal bar: it is encoded U+03F5 ϵ GREEK LUNATE EPSILON SYMBOL. While in normal typography these are just alternative font variants, they may have different meanings as mathematical symbols: computer systems therefore offer distinct encodings for them.[3] In TeX, \epsilon ( ) denotes the lunate form, while \varepsilon ( ) denotes the reversed-3 form. Unicode versions 2.0.0 and onwards use ɛ as the lowercase Greek epsilon letter,[5] but in version 1.0.0, ϵ was used.[6] The lunate or uncial epsilon provided inspiration for the euro sign, €.[7]
There is also a 'Latin epsilon', ⟨ɛ⟩ or "open e", which looks similar to the Greek lowercase epsilon. It is encoded in Unicode as U+025B ɛ LATIN SMALL LETTER OPEN E and U+0190 Ɛ LATIN CAPITAL LETTER OPEN E and is used as an IPA phonetic symbol. This Latin uppercase epsilon, Ɛ, is not to be confused with the Greek uppercase Σ (sigma)
The lunate epsilon, ⟨ϵ⟩, is not to be confused with the set membership symbol ∈. The symbol , first used in set theory and logic by Giuseppe Peano and now used in mathematics in general for set membership ("belongs to"), evolved from the letter epsilon, since the symbol was originally used as an abbreviation for the Latin word est. In addition, mathematicians often read the symbol ∈ as "element of", as in "1 is an element of the natural numbers" for , for example. As late as 1960, ɛ itself was used for set membership, while its negation "does not belong to" (now ∉) was denoted by ε' (epsilon prime).[8] Only gradually did a fully separate, stylized symbol take the place of epsilon in this role. In a related context, Peano also introduced the use of a backwards epsilon, ϶, for the phrase "such that", although the abbreviation s.t. is occasionally used in place of ϶ in informal cardinals.
YouTube Encyclopedic
-
1/5Views:1 156 888315 81768 582188 7621 959 401
-
Epsilon-delta limit definition 1 | Limits | Differential Calculus | Khan Academy
-
epsilon-delta definition ultimate introduction
-
Epsilon Delta Limits in 4 Minutes
-
Proof of a Limit Value Using Epsilon and Delta
-
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus
Transcription
Let me draw a function that would be interesting to take a limit of. And I'll just draw it visually for now, and we'll do some specific examples a little later. So that's my y-axis, and that's my x-axis. And let;s say the function looks something like-- I'll make it a fairly straightforward function --let's say it's a line, for the most part. Let's say it looks just like, accept it has a hole at some point. x is equal to a, so it's undefined there. Let me black that point out so you can see that it's not defined there. And that point there is x is equal to a. This is the x-axis, this is the y is equal f of x-axis. Let's just say that's the y-axis. And let's say that this is f of x, or this is y is equal to f of x. Now we've done a bunch of videos on limits. I think you have an intuition on this. If I were to say what is the limit as x approaches a, and let's say that this point right here is l. We know from our previous videos that-- well first of all I could write it down --the limit as x approaches a of f of x. What this means intuitively is as we approach a from either side, as we approach it from that side, what does f of x approach? So when x is here, f of x is here. When x is here, f of x is there. And we see that it's approaching this l right there. And when we approach a from that side-- and we've done limits where you approach from only the left or right side, but to actually have a limit it has to approach the same thing from the positive direction and the negative direction --but as you go from there, if you pick this x, then this is f of x. f of x is right there. If x gets here then it goes here, and as we get closer and closer to a, f of x approaches this point l, or this value l. So we say that the limit of f of x ax x approaches a is equal to l. I think we have that intuition. But this was not very, it's actually not rigorous at all in terms of being specific in terms of what we mean is a limit. All I said so far is as we get closer, what does f of x get closer to? So in this video I'll attempt to explain to you a definition of a limit that has a little bit more, or actually a lot more, mathematical rigor than just saying you know, as x gets closer to this value, what does f of x get closer to? And the way I think about it's: kind of like a little game. The definition is, this statement right here means that I can always give you a range about this point-- and when I talk about range I'm not talking about it in the whole domain range aspect, I'm just talking about a range like you know, I can give you a distance from a as long as I'm no further than that, I can guarantee you that f of x is go it not going to be any further than a given distance from l --and the way I think about it is, it could be viewed as a little game. Let's say you say, OK Sal, I don't believe you. I want to see you know, whether f of x can get within 0.5 of l. So let's say you give me 0.5 and you say Sal, by this definition you should always be able to give me a range around a that will get f of x within 0.5 of l, right? So the values of f of x are always going to be right in this range, right there. And as long as I'm in that range around a, as long as I'm the range around you give me, f of x will always be at least that close to our limit point. Let me draw it a little bit bigger, just because I think I'm just overriding the same diagram over and over again. So let's say that this is f of x, this is the hole point. There doesn't have to be a hole there; the limit could equal actually a value of the function, but the limit is more interesting when the function isn't defined there but the limit is. So this point right here-- that is, let me draw the axes again. So that's x-axis, y-axis x, y, this is the limit point l, this is the point a. So the definition of the limit, and I'll go back to this in second because now that it's bigger I want explain it again. It says this means-- and this is the epsilon delta definition of limits, and we'll touch on epsilon and delta in a second, is I can guarantee you that f of x, you give me any distance from l you want. And actually let's call that epsilon. And let's just hit on the definition right from the get go. So you say I want to be no more than epsilon away from l. And epsilon can just be any number greater, any real number, greater than 0. So that would be, this distance right here is epsilon. This distance there is epsilon. And for any epsilon you give me, any real number-- so this is, this would be l plus epsilon right here, this would be l minus epsilon right here --the epsilon delta definition of this says that no matter what epsilon one you give me, I can always specify a distance around a. And I'll call that delta. I can always specify a distance around a. So let's say this is delta less than a, and this is delta more than a. This is the letter delta. Where as long as you pick an x that's within a plus delta and a minus delta, as long as the x is within here, I can guarantee you that the f of x, the corresponding f of x is going to be within your range. And if you think about it this makes sense right? It's essentially saying, I can get you as close as you want to this limit point just by-- and when I say as close as you want, you define what you want by giving me an epsilon; on it's a little bit of a game --and I can get you as close as you want to that limit point by giving you a range around the point that x is approaching. And as long as you pick an x value that's within this range around a, long as you pick an x value around there, I can guarantee you that f of x will be within the range you specify. Just make this a little bit more concrete, let's say you say, I want f of x to be within 0.5-- let's just you know, make everything concrete numbers. Let's say this is the number 2 and let's say this is number 1. So we're saying that the limit as x approaches 1 of f of x-- I haven't defined f of x, but it looks like a line with the hole right there, is equal to 2. This means that you can give me any number. Let's say you want to try it out for a couple of examples. Let's say you say I want f of x to be within point-- let me do a different color --I want f of x to be within 0.5 of 2. I want f of x to be between 2.5 and 1.5. Then I could say, OK, as long as you pick an x within-- I don't know, it could be arbitrarily close but as long as you pick an x that's --let's say it works for this function that's between, I don't know, 0.9 and 1.1. So in this case the delta from our limit point is only 0.1. As long as you pick an x that's within 0.1 of this point, or 1, I can guarantee you that your f of x is going to lie in that range. So hopefully you get a little bit of a sense of that. Let me define that with the actual epsilon delta, and this is what you'll actually see in your mat textbook, and then we'll do a couple of examples. And just to be clear, that was just a specific example. You gave me one epsilon and I gave you a delta that worked. But by definition if this is true, or if someone writes this, they're saying it doesn't just work for one specific instance, it works for any number you give me. You can say I want to be within one millionth of, you know, or ten to the negative hundredth power of 2, you know, super close to 2, and I can always give you a range around this point where as long as you pick an x in that range, f of x will always be within this range that you specify, within that were you know, one trillionth of a unit away from the limit point. And of course, the one thing I can't guarantee is what happens when x is equal to a. I'm just saying as long as you pick an x that's within my range but not on a, it'll work. Your f of x will show up to be within the range you specify. And just to make the math clear-- because I've been speaking only in words so far --and this is what we see the textbook: it says look, you give me any epsilon greater than 0. Anyway, this is a definition, right? If someone writes this they mean that you can give them any epsilon greater than 0, and then they'll give you a delta-- remember your epsilon is how close you want f of x to be to your limit point, right? It's a range around f of x --they'll give you a delta which is a range around a, right? Let me write this. So limit as approaches a of f of x is equal to l. So they'll give you a delta where as long as x is no more than delta-- So the distance between x and a, so if we pick an x here-- let me do another color --if we pick an x here, the distance between that value and a, as long as one, that's greater than 0 so that x doesn't show up on top of a, because its function might be undefined at that point. But as long as the distance between x and a is greater than 0 and less than this x range that they gave you, it's less than delta. So as long as you take an x, you know if I were to zoom the x-axis right here-- this is a and so this distance right here would be delta, and this distance right here would be delta --as long as you pick an x value that falls here-- so as long as you pick that x value or this x value or this x value --as long as you pick one of those x values, I can guarantee you that the distance between your function and the limit point, so the distance between you know, when you take one of these x values and you evaluate f of x at that point, that the distance between that f of x and the limit point is going to be less than the number you gave them. And if you think of, it seems very complicated, and I have mixed feelings about where this is included in most calculus curriculums. It's included in like the, you know, the third week before you even learn derivatives, and it's kind of this very mathy and rigorous thing to think about, and you know, it tends to derail a lot of students and a lot of people I don't think get a lot of the intuition behind it, but it is mathematically rigorous. And I think it is very valuable once you study you know, more advanced calculus or become a math major. But with that said, this does make a lot of sense intuitively, right? Because before we were talking about, look you know, I can get you as close as x approaches this value f of x is going to approach this value. And the way we mathematically define it is, you say Sal, I want to be super close. I want the distance to be f of x [UNINTELLIGIBLE]. And I want it to be 0.000000001, then I can always give you a distance around x where this will be true. And I'm all out of time in this video. In the next video I'll do some examples where I prove the limits, where I prove some limit statements using this definition. And hopefully you know, when we use some tangible numbers, this definition will make a little bit more sense. See you in the next video.
History
Origin
The letter ⟨Ε⟩ was adopted from the Phoenician letter He (![]() ) when Greeks first adopted alphabetic writing. In archaic Greek writing, its shape is often still identical to that of the Phoenician letter. Like other Greek letters, it could face either leftward or rightward (
) when Greeks first adopted alphabetic writing. In archaic Greek writing, its shape is often still identical to that of the Phoenician letter. Like other Greek letters, it could face either leftward or rightward (![]()
![]() ), depending on the current writing direction, but, just as in Phoenician, the horizontal bars always faced in the direction of writing. Archaic writing often preserves the Phoenician form with a vertical stem extending slightly below the lowest horizontal bar. In the classical era, through the influence of more cursive writing styles, the shape was simplified to the current ⟨E⟩ glyph.[9]
), depending on the current writing direction, but, just as in Phoenician, the horizontal bars always faced in the direction of writing. Archaic writing often preserves the Phoenician form with a vertical stem extending slightly below the lowest horizontal bar. In the classical era, through the influence of more cursive writing styles, the shape was simplified to the current ⟨E⟩ glyph.[9]
Sound value
While the original pronunciation of the Phoenician letter He was [h], the earliest Greek sound value of Ε was determined by the vowel occurring in the Phoenician letter name, which made it a natural choice for being reinterpreted from a consonant symbol to a vowel symbol denoting an [e] sound.[10] Besides its classical Greek sound value, the short /e/ phoneme, it could initially also be used for other [e]-like sounds. For instance, in early Attic before c. 500 BC, it was used also both for the long, open /ɛː/, and for the long close /eː/. In the former role, it was later replaced in the classic Greek alphabet by Eta (⟨Η⟩), which was taken over from eastern Ionic alphabets, while in the latter role it was replaced by the digraph spelling ΕΙ.
Epichoric alphabets
Some dialects used yet other ways of distinguishing between various e-like sounds.
In Corinth, the normal function of ⟨Ε⟩ to denote /e/ and /ɛː/ was taken by a glyph resembling a pointed B (![]() ), while ⟨Ε⟩ was used only for long close /eː/.[11] The letter Beta, in turn, took the deviant shape
), while ⟨Ε⟩ was used only for long close /eː/.[11] The letter Beta, in turn, took the deviant shape ![]() .
.
In Sicyon, a variant glyph resembling an ⟨X⟩ (![]() ) was used in the same function as Corinthian
) was used in the same function as Corinthian ![]() .[12]
.[12]
In Thespiai (Boeotia), a special letter form consisting of a vertical stem with a single rightward-pointing horizontal bar (![]() ) was used for what was probably a raised variant of /e/ in pre-vocalic environments.[13][14] This tack glyph was used elsewhere also as a form of "Heta", i.e. for the sound /h/.
) was used for what was probably a raised variant of /e/ in pre-vocalic environments.[13][14] This tack glyph was used elsewhere also as a form of "Heta", i.e. for the sound /h/.
Glyph variants
After the establishment of the canonical classical Ionian (Euclidean) Greek alphabet, new glyph variants for Ε were introduced through handwriting. In the uncial script (used for literary papyrus manuscripts in late antiquity and then in early medieval vellum codices), the "lunate" shape (![]() ) became predominant. In cursive handwriting, a large number of shorthand glyphs came to be used, where the cross-bar and the curved stroke were linked in various ways.[15] Some of them resembled a modern lowercase Latin "e", some a "6" with a connecting stroke to the next letter starting from the middle, and some a combination of two small "c"-like curves. Several of these shapes were later taken over into minuscule book hand. Of the various minuscule letter shapes, the inverted-3 form became the basis for lower-case Epsilon in Greek typography during the modern era.
) became predominant. In cursive handwriting, a large number of shorthand glyphs came to be used, where the cross-bar and the curved stroke were linked in various ways.[15] Some of them resembled a modern lowercase Latin "e", some a "6" with a connecting stroke to the next letter starting from the middle, and some a combination of two small "c"-like curves. Several of these shapes were later taken over into minuscule book hand. Of the various minuscule letter shapes, the inverted-3 form became the basis for lower-case Epsilon in Greek typography during the modern era.
| Uncial | Uncial variants | Cursive variants | Minuscule | Minuscule with ligatures |
|---|---|---|---|---|
Uses
International Phonetic Alphabet
Despite its pronunciation as mid, in the International Phonetic Alphabet, the Latin epsilon /ɛ/ represents open-mid front unrounded vowel, as in the English word pet /pɛt/.
Symbol
The uppercase Epsilon is not commonly used outside of the Greek language because of its similarity to the Latin letter E. However, it is commonly used in structural mechanics with Young's Modulus equations for calculating tensile, compressive and areal strain.
The Greek lowercase epsilon ε, the lunate epsilon symbol ϵ, and the Latin lowercase epsilon ɛ (see above) are used in a variety of places:
- In engineering mechanics, strain calculations ϵ = increase of length / original length. Usually this relates to extensometer testing of metallic materials.
- In mathematics
- (In early calculus or nonstandard analysis) An infinitesimally small positive quantity is commonly denoted ε.
- (In analysis) By extension, a quantity thought of as "small," "negligible," or, especially, "arbitrarily small," is often denoted ε. For instance, quantities subject to a limit which takes them towards zero are often denoted ε; see (ε, δ)-definition of limit.
- Hilbert introduced epsilon terms as an extension to first-order logic; see epsilon calculus.
- it is used to represent the Levi-Civita symbol.
- it is used to represent dual numbers: , with and .
- it is sometimes used to denote the Heaviside step function.[16]
- in set theory, the epsilon numbers are ordinal numbers that satisfy the fixed point ε = ωε. The first epsilon number, ε0, is the limit ordinal of the set {ω, ωω, ωωω, ...}.
- in numerical analysis and statistics it is used as the error term
- in group theory it is used as the idempotent group when e is in use as a variable name
- (In early calculus or nonstandard analysis) An infinitesimally small positive quantity is commonly denoted ε.
- In computer science
- it often represents the empty string, though different writers use a variety of other symbols for the empty string as well; usually the lower-case Greek letter lambda (λ).
- the machine epsilon indicates the upper bound on the relative error due to rounding in floating point arithmetic.
- In physics,
- it indicates the permittivity of a medium; with the subscript 0 (ε0) it is the permittivity of free space.
- it can also indicate the strain of a material (a ratio of extensions).
- In automata theory, it shows a transition that involves no shifting of an input symbol.
- In astronomy,
- it stands for the fifth-brightest star in a constellation (see Bayer designation).
- Epsilon is the name for the most distant and most visible ring of Uranus.
- In planetary science, ε denotes the axial tilt.
- In chemistry, it represents the molar extinction coefficient of a chromophore.
- In economics, ε refers to elasticity.
- In statistics,
- it is used to refer to error terms.
- it also can to refer to the degree of sphericity in repeated measures ANOVAs.
- In agronomy, it is used to represent the "photosynthetic efficiency" of a particular plant or crop.
Unicode
- Greek Epsilon
| Preview | Ε | ε | ϵ | ϶ | ||||
|---|---|---|---|---|---|---|---|---|
| Unicode name | GREEK CAPITAL LETTER EPSILON | GREEK SMALL LETTER EPSILON | GREEK LUNATE EPSILON SYMBOL | GREEK REVERSED LUNATE EPSILON SYMBOL | ||||
| Encodings | decimal | hex | dec | hex | dec | hex | dec | hex |
| Unicode | 917 | U+0395 | 949 | U+03B5 | 1013 | U+03F5 | 1014 | U+03F6 |
| UTF-8 | 206 149 | CE 95 | 206 181 | CE B5 | 207 181 | CF B5 | 207 182 | CF B6 |
| Numeric character reference | Ε |
Ε |
ε |
ε |
ϵ |
ϵ |
϶ |
϶ |
| Named character reference | Ε | ε, ε | ϵ, ϵ, ϵ | ϶, ϶ | ||||
| DOS Greek | 132 | 84 | 156 | 9C | ||||
| DOS Greek-2 | 168 | A8 | 222 | DE | ||||
| Windows 1253 | 197 | C5 | 229 | E5 | ||||
| TeX | \varepsilon | \epsilon | ||||||
- Coptic Eie
| Preview | Ⲉ | ⲉ | ||
|---|---|---|---|---|
| Unicode name | COPTIC CAPITAL LETTER EIE | COPTIC SMALL LETTER EIE | ||
| Encodings | decimal | hex | dec | hex |
| Unicode | 11400 | U+2C88 | 11401 | U+2C89 |
| UTF-8 | 226 178 136 | E2 B2 88 | 226 178 137 | E2 B2 89 |
| Numeric character reference | Ⲉ |
Ⲉ |
ⲉ |
ⲉ |
| Preview | Ɛ | ɛ | ᶓ | ᵋ | ||||
|---|---|---|---|---|---|---|---|---|
| Unicode name | LATIN CAPITAL LETTER OPEN E |
LATIN SMALL LETTER OPEN E |
LATIN SMALL LETTER OPEN E WITH RETROFLEX HOOK |
MODIFIER LETTER SMALL OPEN E | ||||
| Encodings | decimal | hex | dec | hex | dec | hex | dec | hex |
| Unicode | 400 | U+0190 | 603 | U+025B | 7571 | U+1D93 | 7499 | U+1D4B |
| UTF-8 | 198 144 | C6 90 | 201 155 | C9 9B | 225 182 147 | E1 B6 93 | 225 181 139 | E1 B5 8B |
| Numeric character reference | Ɛ |
Ɛ |
ɛ |
ɛ |
ᶓ |
ᶓ |
ᵋ |
ᵋ |
| Preview | ɜ | ɝ | ᶔ | ᶟ | ||||
|---|---|---|---|---|---|---|---|---|
| Unicode name | LATIN SMALL LETTER REVERSED OPEN E |
LATIN SMALL LETTER REVERSED OPEN E WITH HOOK |
LATIN SMALL LETTER REVERSED OPEN E WITH RETROFLEX HOOK |
MODIFIER LETTER SMALL REVERSED OPEN E | ||||
| Encodings | decimal | hex | dec | hex | dec | hex | dec | hex |
| Unicode | 604 | U+025C | 605 | U+025D | 7572 | U+1D94 | 7583 | U+1D9F |
| UTF-8 | 201 156 | C9 9C | 201 157 | C9 9D | 225 182 148 | E1 B6 94 | 225 182 159 | E1 B6 9F |
| Numeric character reference | ɜ |
ɜ |
ɝ |
ɝ |
ᶔ |
ᶔ |
ᶟ |
ᶟ |
| Preview | ᴈ | ᵌ | ʚ | ɞ | ||||
|---|---|---|---|---|---|---|---|---|
| Unicode name | LATIN SMALL LETTER TURNED OPEN E |
MODIFIER LETTER SMALL TURNED OPEN E |
LATIN SMALL LETTER CLOSED OPEN E |
LATIN SMALL LETTER CLOSED REVERSED OPEN E | ||||
| Encodings | decimal | hex | dec | hex | dec | hex | dec | hex |
| Unicode | 7432 | U+1D08 | 7500 | U+1D4C | 666 | U+029A | 606 | U+025E |
| UTF-8 | 225 180 136 | E1 B4 88 | 225 181 140 | E1 B5 8C | 202 154 | CA 9A | 201 158 | C9 9E |
| Numeric character reference | ᴈ |
ᴈ |
ᵌ |
ᵌ |
ʚ |
ʚ |
ɞ |
ɞ |
- Mathematical Epsilon
| Preview | 𝚬 | 𝛆 | 𝛦 | 𝜀 | 𝜠 | 𝜺 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Unicode name | MATHEMATICAL BOLD CAPITAL EPSILON |
MATHEMATICAL BOLD SMALL EPSILON |
MATHEMATICAL ITALIC CAPITAL EPSILON |
MATHEMATICAL ITALIC SMALL EPSILON |
MATHEMATICAL BOLD ITALIC CAPITAL EPSILON |
MATHEMATICAL BOLD ITALIC SMALL EPSILON | ||||||
| Encodings | decimal | hex | dec | hex | dec | hex | dec | hex | dec | hex | dec | hex |
| Unicode | 120492 | U+1D6AC | 120518 | U+1D6C6 | 120550 | U+1D6E6 | 120576 | U+1D700 | 120608 | U+1D720 | 120634 | U+1D73A |
| UTF-8 | 240 157 154 172 | F0 9D 9A AC | 240 157 155 134 | F0 9D 9B 86 | 240 157 155 166 | F0 9D 9B A6 | 240 157 156 128 | F0 9D 9C 80 | 240 157 156 160 | F0 9D 9C A0 | 240 157 156 186 | F0 9D 9C BA |
| UTF-16 | 55349 57004 | D835 DEAC | 55349 57030 | D835 DEC6 | 55349 57062 | D835 DEE6 | 55349 57088 | D835 DF00 | 55349 57120 | D835 DF20 | 55349 57146 | D835 DF3A |
| Numeric character reference | 𝚬 |
𝚬 |
𝛆 |
𝛆 |
𝛦 |
𝛦 |
𝜀 |
𝜀 |
𝜠 |
𝜠 |
𝜺 |
𝜺 |
| Preview | 𝛜 | 𝜖 | 𝝐 | |||
|---|---|---|---|---|---|---|
| Unicode name | MATHEMATICAL BOLD EPSILON SYMBOL |
MATHEMATICAL ITALIC EPSILON SYMBOL |
MATHEMATICAL BOLD ITALIC EPSILON SYMBOL | |||
| Encodings | decimal | hex | dec | hex | dec | hex |
| Unicode | 120540 | U+1D6DC | 120598 | U+1D716 | 120656 | U+1D750 |
| UTF-8 | 240 157 155 156 | F0 9D 9B 9C | 240 157 156 150 | F0 9D 9C 96 | 240 157 157 144 | F0 9D 9D 90 |
| UTF-16 | 55349 57052 | D835 DEDC | 55349 57110 | D835 DF16 | 55349 57168 | D835 DF50 |
| Numeric character reference | 𝛜 |
𝛜 |
𝜖 |
𝜖 |
𝝐 |
𝝐 |
| Preview | 𝝚 | 𝝴 | 𝞔 | 𝞮 | ||||
|---|---|---|---|---|---|---|---|---|
| Unicode name | MATHEMATICAL SANS-SERIF BOLD CAPITAL EPSILON |
MATHEMATICAL SANS-SERIF BOLD SMALL EPSILON |
MATHEMATICAL SANS-SERIF BOLD ITALIC CAPITAL EPSILON |
MATHEMATICAL SANS-SERIF BOLD ITALIC SMALL EPSILON | ||||
| Encodings | decimal | hex | dec | hex | dec | hex | dec | hex |
| Unicode | 120666 | U+1D75A | 120692 | U+1D774 | 120724 | U+1D794 | 120750 | U+1D7AE |
| UTF-8 | 240 157 157 154 | F0 9D 9D 9A | 240 157 157 180 | F0 9D 9D B4 | 240 157 158 148 | F0 9D 9E 94 | 240 157 158 174 | F0 9D 9E AE |
| UTF-16 | 55349 57178 | D835 DF5A | 55349 57204 | D835 DF74 | 55349 57236 | D835 DF94 | 55349 57262 | D835 DFAE |
| Numeric character reference | 𝝚 |
𝝚 |
𝝴 |
𝝴 |
𝞔 |
𝞔 |
𝞮 |
𝞮 |
| Preview | 𝞊 | 𝟄 | ||
|---|---|---|---|---|
| Unicode name | MATHEMATICAL SANS-SERIF BOLD EPSILON SYMBOL |
MATHEMATICAL SANS-SERIF BOLD ITALIC EPSILON SYMBOL | ||
| Encodings | decimal | hex | dec | hex |
| Unicode | 120714 | U+1D78A | 120772 | U+1D7C4 |
| UTF-8 | 240 157 158 138 | F0 9D 9E 8A | 240 157 159 132 | F0 9D 9F 84 |
| UTF-16 | 55349 57226 | D835 DF8A | 55349 57284 | D835 DFC4 |
| Numeric character reference | 𝞊 |
𝞊 |
𝟄 |
𝟄 |
These characters are used only as mathematical symbols. Stylized Greek text should be encoded using the normal Greek letters, with markup and formatting to indicate text style.
Initial
-
-
folio 64 verso
-
folio 125 verso
See also
- Е and е, the letter Ye of the Cyrillic alphabet
- Є є, Ukrainian Ye
- Ԑ ԑ, Reversed Ze
- E (disambiguation)
References
- ^ Wells, John C. (1990). "epsilon". Longman Pronunciation Dictionary. Harlow, England: Longman. p. 250. ISBN 0582053838.
- ^ "epsilon". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
- ^ a b Nick Nicholas: Letters Archived 2012-12-15 at archive.today, 2003–2008. (Greek Unicode Issues)
- ^ Colwell, Ernest C. (1969). "A chronology for the letters Ε, Η, Λ, Π in the Byzantine minuscule book hand". Studies in methodology in textual criticism of the New Testament. Leiden: Brill. p. 127.
- ^ "Code Charts" (PDF). The Unicode Standard, Version 2.0. p. 130. ISBN 0-201-48345-9.
- ^ "Code Charts" (PDF). The Unicode Standard, Version 1.0. Vol. 1. p. 130. ISBN 0-201-56788-1.
- ^ "European Commission – Economic and Financial Affairs – How to use the euro name and symbol". Ec.europa.eu. Retrieved 7 April 2010.
Inspiration for the € symbol itself came from the Greek epsilon, ϵ – a reference to the cradle of European civilization – and the first letter of the word Europe, crossed by two parallel lines to 'certify' the stability of the euro.
- ^ Halmos, Paul R. (1960). Naive Set Theory. New York: Van Nostrand. pp. 5–6. ISBN 978-1614271314.
- ^ Jeffery, Lilian H. (1961). The local scripts of archaic Greece. Oxford: Clarendon. pp. 63–64.
- ^ Jeffery, Local scripts, p. 24.
- ^ Jeffery, Local scripts, p. 114.
- ^ Jeffery, Local scripts, p. 138.
- ^ Nicholas, Nick (2005). "Proposal to add Greek epigraphical letters to the UCS" (PDF). Archived from the original (PDF) on February 17, 2006. Retrieved 2010-08-12.
- ^ Jeffery, Local scripts, p. 89.
- ^ Thompson, Edward M. (1911). An introduction to Greek and Latin palaeography. Oxford: Clarendon. pp. 191–194.
- ^ Weisstein, Eric W. "Delta Function". mathworld.wolfram.com. Retrieved 2019-02-19.
Further reading
- Hoffman, Paul; The Man Who Loved Only Numbers. Hyperion, 1998. ISBN 0-7868-6362-5.









