Argument of periapsis

Part of a series on
Astrodynamics
Orbital mechanics
Orbital elements Apsis Argument of periapsis Eccentricity Inclination Mean anomaly Orbital nodes Semi-major axis True anomaly
Types of two-body orbits by eccentricity Circular orbit Elliptic orbit Transfer orbit (Hohmann transfer orbit Bi-elliptic transfer orbit) Parabolic orbit Hyperbolic orbit Radial orbit Decaying orbit
Equations Dynamical friction Escape velocity Kepler's equation Kepler's laws of planetary motion Orbital period Orbital velocity Surface gravity Specific orbital energy Vis-viva equation
Celestial mechanics
Gravitational influences Barycenter Hill sphere Perturbations Sphere of influence
N-body orbits Lagrangian points (Halo orbits) Lissajous orbits Lyapunov orbits
Engineering and efficiency
Preflight engineering Mass ratio Payload fraction Propellant mass fraction Tsiolkovsky rocket equation
Efficiency measures Gravity assist Oberth effect
Propulsive maneuvers Orbital maneuver Orbit insertion
v t e

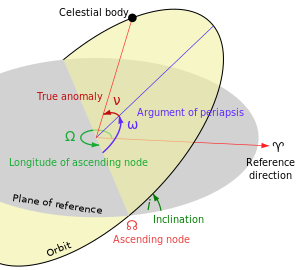
The argument of periapsis (also called argument of perifocus or argument of pericenter), symbolized as ω (omega), is one of the orbital elements of an orbiting body. Parametrically, ω is the angle from the body's ascending node to its periapsis, measured in the direction of motion.

For specific types of orbits, terms such as argument of perihelion (for heliocentric orbits), argument of perigee (for geocentric orbits), argument of periastron (for orbits around stars), and so on, may be used (see apsis for more information).

An argument of periapsis of 0° means that the orbiting body will be at its closest approach to the central body at the same moment that it crosses the plane of reference from South to North. An argument of periapsis of 90° means that the orbiting body will reach periapsis at its northmost distance from the plane of reference.

Adding the argument of periapsis to the longitude of the ascending node gives the longitude of the periapsis. However, especially in discussions of binary stars and exoplanets, the terms "longitude of periapsis" or "longitude of periastron" are often used synonymously with "argument of periapsis".

Calculation

In astrodynamics the argument of periapsis ω can be calculated as follows:

${\displaystyle \omega =\arccos {{\mathbf {n} \cdot \mathbf {e} } \over {\mathbf {\left|n\right|} \mathbf {\left|e\right|} }}}$

If e_z < 0 then ω → 2π − ω.

where:

• n is a vector pointing towards the ascending node (i.e. the z-component of n is zero),
• e is the eccentricity vector (a vector pointing towards the periapsis).

In the case of equatorial orbits (which have no ascending node), the argument is strictly undefined. However, if the convention of setting the longitude of the ascending node Ω to 0 is followed, then the value of ω follows from the two-dimensional case:

$${\displaystyle \omega =\mathrm {atan2} \left(e_{y},e_{x}\right)}$$

If the orbit is clockwise (i.e. (r × v)_z < 0) then ω → 2π − ω.

where:

• e_x and e_y are the x- and y-components of the eccentricity vector e.

In the case of circular orbits it is often assumed that the periapsis is placed at the ascending node and therefore ω = 0. However, in the professional exoplanet community, ω = 90° is more often assumed for circular orbits, which has the advantage that the time of a planet's inferior conjunction (which would be the time the planet would transit if the geometry were favorable) is equal to the time of its periastron.^[1][2][3]

See also

• Apsidal precession
• Kepler orbit
• Orbital mechanics
• Orbital node

References

External links

• Argument Of Perihelion in Swinburne University Astronomy Website

This page was last edited on 28 May 2024, at 05:14