Центр окружности девяти точек

Центр окружности девяти точек
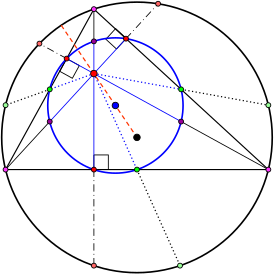Треугольник, описанная вокруг него окружность (черная) и её центр (чёрный), высоты треугольника (часть высоты, расположенная внутри окружности Эйлера, синяя, а вне - её черная) и окружность девяти точек (синяя) и её центр (синий)
Барицентрические координаты	${\displaystyle a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}:}$${\displaystyle b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}:}$${\displaystyle c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}}$
Трилинейные координаты	${\displaystyle \cos(B-C):\cos(C-A):\cos(A-B)}$
Код ЭЦТ	X(5)
Связанные точки
Изогонально сопряженная	точка Косниты

Центр окружности девяти точек — одна из замечательных точек треугольника. Её часто обозначают как ${\displaystyle O_{9}}$.

Окружность девяти точек, или окружность Эйлера, проходит через девять важных точек треугольника — середины сторон, основания трёх высот и середины отрезков, соединяющих ортоцентр с вершинами треугольника. Центр этой окружности указан как точка X(5) в энциклопедии центров треугольника Кларка Кимберлинга^[1][2].

Свойства

• Центр окружности девяти точек ${\displaystyle O_{9}}$ лежит на прямой Эйлера треугольника посредине между ортоцентром ${\displaystyle H}$ и центром описанной окружности ${\displaystyle O}$. Центроид ${\displaystyle M}$ также лежит на этой линии на расстоянии 2/3 от ортоцентра к центру описанной окружности^[2][3], так, что

${\displaystyle O_{9}O=O_{9}H=3O_{9}M~.}$

Таким образом, если пара из этих четырёх центров известна, положение двух других легко найти.

• Андрю Гинанд (Andrew Guinand) в 1984-м году, исследуя задачу, ныне известную как задача определения треугольника Эйлера, показал, что если положение этих центров для неизвестного треугольника задано, то инцентр треугольника лежит внутри ортоцентроидальной окружности^[en] (окружности, диаметром которой служит отрезок между центроидом и ортоцентром). Только одна точка внутри этой окружности не может быть центром вписанной окружности — это центр девяти точек. Любая другая точка внутри этой окружности определяет единственный треугольник^[4][5][6][7].
• Расстояние от центра окружности девяти точек до инцентра ${\displaystyle I}$ удовлетворяет формулам:

${\displaystyle IO_{9}<{\dfrac {1}{2}}IO~,}$

${\displaystyle IO_{9}={\dfrac {1}{2}}(R-2r)<{\frac {R}{2}}~,}$

${\displaystyle 2R\cdot IO_{9}=OI^{2}~,}$

где ${\displaystyle R}$ и ${\displaystyle r}$ — радиусы описанной и вписанной окружностей соответственно.

• Центр окружности девяти точек является центром описанных окружностей серединного треугольника, ортотреугольника и треугольника Эйлера^[8][3]. Вообще говоря, эта точка является центром описанной окружности треугольника, имеющего в качестве вершин любые три из девяти перечисленных точек.
• Центр окружности девяти точек совпадает с центроидом четырёх точек — трёх точек треугольника и его ортоцентра^[9].
• Из девяти точек на окружности Эйлера три являются серединами отрезков, соединяющих вершины с ортоцентром (вершины треугольника Эйлера-Фейербаха). Эти три точки являются отражениями середин сторон треугольника относительно центра окружности девяти точек.
• Таким образом, центр окружности девяти точек служит центром симметрии, переводящим серединный треугольник в треугольник Эйлера-Фейербаха (и наоборот) ^[3].
• Согласно теореме Лестера центр окружности девяти точек лежит на одной окружности с тремя другими точками — двумя точками Ферма и центром описанной окружности ^[10].

• Точка Косниты треугольника, связанная с теоремой Косниты, изогонально сопряжена центру окружности девяти точек^[11]. (см. рис.)
• Прямая ${\displaystyle X(485)X(486)}$, проходящая через две точки Вектена ${\displaystyle X(485)}$ и ${\displaystyle X(486)}$, пересекает прямую Эйлера в центре девяти точек треугольника ${\displaystyle ABC}$.

Координаты

Трилинейные координаты центра окружности девяти точек равны^[1][2]:

${\displaystyle \cos(B-C):\cos(C-A):\cos(A-B)}$

${\displaystyle =\cos A+2\cos B\cos C:\cos B+2\cos C\cos A:\cos C+2\cos A\cos B}$

${\displaystyle =\cos A-2\sin B\sin C:\cos B-2\sin C\sin A:\cos C-2\sin A\sin B}$

${\displaystyle =bc[a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}]:ca[b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}]:ab[c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}]~.}$

Барицентрические координаты центра равны^[2]:

${\displaystyle a\cos(B-C):b\cos(C-A):c\cos(A-B)}$

${\displaystyle =a^{2}(b^{2}+c^{2})-(b^{2}-c^{2})^{2}:b^{2}(c^{2}+a^{2})-(c^{2}-a^{2})^{2}:c^{2}(a^{2}+b^{2})-(a^{2}-b^{2})^{2}~.}$

Примечания

Литература

• Kimberling. Central Points and Central Lines in the Plane of a Triangle // Mathematics Magazine. — 1994. — Т. 67, вып. 3. — JSTOR 2690608.
• Stern. Euler’s triangle determination problem // Forum Geometricorum. — 2007. — Т. 7.
• Dekov. Nine-point center // Journal of Computer-Generated Euclidean Geometry. — 2007.
• Euler. Solutio facilis problematum quorundam geometricorum difficillimorum (Latin) // Novi Commentarii academiae scientiarum Petropolitanae. — 1767. — Т. 11.
• Andrew P. Guinand. Euler lines, tritangent centers, and their triangles // American Mathematical Monthly. — 1984. — Т. 91, вып. 5. — JSTOR 2322671.
• William N. Franzsen. The distance from the incenter to the Euler line // Forum Geometricorum. — 2011. — Вып. 11.
• Paul Yiu. The circles of Lester, Evans, Parry, and their generalizations // Forum Geometricorum. — 2010. — Т. 10.

• Rigby. Brief notes on some forgotten geometrical theorems // Mathematics and Informatics Quarterly. — 1997. — Vol. 7.

Ссылки

• Weisstein, Eric W. Nine-Point Center (англ.) на сайте Wolfram MathWorld.

Эта страница в последний раз была отредактирована 28 декабря 2023 в 05:03.