Радикальная ось двух окружностей

Радика́льная ось двух окружностей — геометрическое место точек, степени которых относительно двух заданных окружностей равны. Иными словами, равны длины четырёх касательных, проведенных к двум данным окружностям из любой точки M данного геометрического места точек.

Радикальная ось двух окружностей существует тогда и только тогда, когда окружности неконцентрические, и может быть определена как для окружностей, так и для точек (окружностей нулевого радиуса) и мнимых окружностей (мнимого радиуса).

Свойства радикальной оси

Радикальная ось является прямой. Поскольку степень точки относительно окружности равна $x^{2}+y^{2}+Ax+By+C,$ где коэффициенты A, B и C определяются через координаты центра и радиус окружности, то, приравняв степени точки относительно двух окружностей, получим $x^{2}+y^{2}+A_{1}x+B_{1}y+C_{1}=x^{2}+y^{2}+A_{2}x+B_{2}y+C_{2}\Leftrightarrow (A_{1}-A_{2})x+(B_{1}-B_{2})y+(C_{1}-C_{2})=0,$ а это уравнение прямой. Существует также доказательство этого факта с использованием только геометрических методов.
Радикальная ось перпендикулярна линии центров, что следует из симметричности обеих окружностей относительно линии центров.
Если P — точка на радикальной оси, то длины касательных из точки P к обеим окружностям равны — это следует из того, что степень точки равна квадрату длины отрезка касательной. В частности, радикальная ось делит пополам отрезки общих касательных.

Если окружности пересекаются в двух точках, то их радикальной осью будет прямая, проходящая через эти точки, если они касаются внешним образом — то радикальной осью будет общая внутренняя касательная, если внутренним — то общая касательная (единственная).

Если прямые, содержащие хорды $AB$ и $CD$ первой и второй окружности соответственно пересекаются на радикальной оси, то четырёхугольник $ABCD$ вписанный. Это несложно доказать: пусть $P$ — точка пересечения. По свойству степени точки, она равна $PA\cdot PB,$ а так как P лежит на радикальной оси, то она равна и $PC\cdot PD.$ Так как $PA\cdot PB=PC\cdot PD,$ то точки $A,B,C$ и $D$ лежат на одной окружности. Верно и обратное: если две окружности пересечь третьей так, что $AB$ — общая хорда первой и третьей, а $CD$ — общая хорда второй и третьей, то прямые AB и CD пересекутся на радикальной оси первых двух окружностей, причём в так называемом радикальном центре трёх окружностей (см. ниже). На этом свойстве основано построение радикальной оси циркулем и линейкой: построим окружность, пересекающую две данные в четырёх точках, а затем опустим из их радикального центра перпендикуляр на линию центров.

Радикальные оси трёх окружностей с неколлинеарными центрами пересекаются в одной точке, называемой радикальным центром. Пусть $\Omega _{1},\Omega _{2},\Omega _{3}$ — окружности, а $P$ — точка пересечения радикальной оси окружностей $\Omega _{1}$ и $\Omega _{2}$ с радикальной осью окружностей $\Omega _{2}$ и $\Omega _{3}$ . Если ${\mathfrak {P}}(\omega ,A)$ — степень точки $A$ относительно окружности $\omega ,$ то по определению радикальной оси ${\mathfrak {P}}(\Omega _{1},P)={\mathfrak {P}}(\Omega _{2},P)={\mathfrak {P}}(\Omega _{3},P),$ и точка $P$ лежит на радикальной оси окружностей $\Omega _{1}$ и $\Omega _{3}.$
Геометрическое место центров окружностей, ортогональных двум данным, есть их радикальная ось с исключённой общей хордой (если она есть). См. рис.

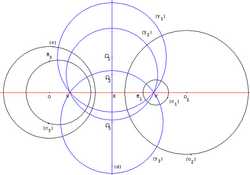
Антигомологические хорды^{[уточнить]} двух окружностей пересекаются на их радикальной оси (видимо, имеются в виду две хорды, проходящие через две пары антигомотетических точек двух окружностей, см. рис. ниже).
Пусть $ABCD$ — четырёхугольник, прямые $AB$ и $CD$ пересекаются в точке $F$ , $BC$ и $AD$ — в $E$ . Тогда окружности, построенные на отрезках $AC$ , $BD$ и $EF$ , как на диаметрах, имеют общую радикальную ось, на которой лежат точки пересечения высот треугольников $ABE$ , $CDE$ , $BCF$ и $ADF$ (прямая Обера — Штейнера).

Ортогональность

Две окружности, пересекающиеся под прямым углом, называются ортогональными. Окружности можно считать ортогональными, если они образуют прямой угол друг с другом.
Две пересекающиеся в точках A и B окружности с центрами O и O' называются ортогональными, если являются прямыми углы OAO' и OBO' . Именно это условие гарантирует прямой угол между окружностями. В этом случае перпендикулярны радиусы (нормали) двух окружностей, проведенные в точку их пересечения. Следовательно, перпендикулярны и касательные двух окружностей, проведенные в точку их пересечения. Касательная окружности перпендикулярна радиусу (нормали), проведенному в точку касания. Обычно угол между кривыми — это угол между их касательными, проведенными в точке их пересечения.
Возможно другое дополнительное условие. Пусть две пересекающиеся в точках A и B окружности имеют середины пресекающихся дуг в точках C и D, то есть дуга AС равна дуге СB, дуга AD равна дуге DB. Тогда эти окружности называются ортогональными, если являются прямыми углы СAD и СBD.

Построение радикальной оси двух непересекающхся окружностей. Пояснения на рисунке. Радикальная ось показана красной

Следствия из свойств радикальной оси

На прямой, проходящей через точки касания двух вневписанных окружностей треугольника с двумя его сторонами, эти вневписанные окружности отсекают равные отрезки.
Последнее можно сформулировать так. Если 2 вневписанные окружности треугольника касаются 2 его разных сторон и 2 их продолжений в 4 точках касания, то образуемый 4 последними точками, как вершинами, четырехугольник есть равнобокая трапеция, у которой равны 2 боковые стороны, а также равны две диагонали (касательные к 2 окружностям).
Диагонали описанного около окружности шестиугольника, соединяющие противоположные вершины, пересекаются в одной точке (теорема Брианшона для окружности).