Основная теорема о рекуррентных соотношениях

Основная теорема о рекуррентных соотношениях используется в анализе алгоритмов для получения асимптотической оценки рекурсивных соотношений (рекуррентных уравнений), часто возникающих при анализе алгоритмов типа «разделяй и властвуй», например, при оценке времени их выполнения. Теорема была введена и доказана Джоном Бентли, Доротеном Хакеном и Джеймсом Хакеном в 1980 году. Теорема была популяризована в книге Алгоритмы: построение и анализ (Томас Кормен, Чарльз Лейзерстон, Рональд Ривест, Клиффорд Штайн), в которой она была приведена.

Не все рекурсивные соотношения могут быть решены с помощью основной теоремы. Существует несколько её обобщений, в том числе метод Акры — Бацци^[en].

Описание

Рассмотрим задачу, которую можно решить рекурсивным алгоритмом:

function T(input n: размер задачи):
  if n < некоторая константа k:
    решить задачу относительно n нерекурсивно
  else:
    определить множество из a подзадач, каждая размера n/b
    вызвать функцию T рекурсивно для каждой подзадачи
    объединить решения
end

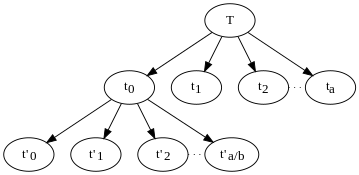
В приведённом примере алгоритм рекурсивно разделяет исходную задачу размера n на несколько новых подзадач, каждая размером n/b. Такое разбиение может быть представлено в виде дерева вызовов, в котором каждый узел соответствует рекурсивному вызову, а ветви, исходящие из узла — последующим вызовам для подзадач. Каждый узел будет иметь a ветвей. Также в каждом узле производится объём работы, соответствующий размеру текущей подзадачи n (переданному в данный вызов функции) согласно соотношению ${\displaystyle f(n)}$. Общий объём работы алгоритма определяется как сумма всех работ в узлах данного дерева.

Вычислительная сложность подобных алгоритмов может быть представлена в виде рекуррентного соотношения ${\displaystyle T(n)=a\,T\left({\frac {n}{b}}\right)+f(n)}$. Его можно решить путём многократных подстановок выражения ${\displaystyle T\left({\frac {n}{b}}\right)}$.^[1]

С помощью основной теоремы возможно быстрое вычисление подобных соотношений, что позволяет получить асимптотическую оценку времени работы рекурсивных алгоритмов в нотации O(n) (Θ-нотации), не производя подстановок.

Общая форма

Основная теорема рассматривает следующие рекуррентные соотношения:

${\displaystyle T(n)=a\,T\left({\frac {n}{b}}\right)+f(n),\quad {\text{где}}~a\geqslant 1,\ b>1.}$

В применении к анализу алгоритмов константы и функции обозначают:

n — размер задачи.

a — количество подзадач в рекурсии.

n/b — размер каждой подзадачи. (Предполагается, что все подзадачи на каждом этапе имеют одинаковый размер.)

f (n) — оценка сложности работы, производимой алгоритмом вне рекурсивных вызовов. В неё также включается вычислительная стоимость деления на подзадачи и объединения результатов решения подзадач.

Основная теорема позволяет получить асимптотическую оценку для следующих трёх случаев:

Вариант 1

Общая форма

Если ${\displaystyle f(n)=O(n^{c})}$, и выполняется соотношение ${\displaystyle c<\log _{b}a}$, тогда:

${\displaystyle T(n)=\Theta \left(n^{\log _{b}a}\right).}$

Пример

${\displaystyle T(n)=8T\left({\frac {n}{2}}\right)+1000n^{2}.}$

Согласно формуле, значения констант и сложности нерекурсивной части задачи:

${\displaystyle a=8,\ b=2,\ f(n)=1000n^{2},}$

${\displaystyle f(n)=O(n^{c})}$, где ${\displaystyle c=2}$.

Затем проверяем, выполняется ли соотношение 1-го варианта:

${\displaystyle \log _{b}a=\log _{2}8=3>c}$.

Следовательно,

${\displaystyle T(n)=\Theta \left(n^{\log _{b}a}\right)=\Theta (n^{3}).}$

(Для данного примера точное решение рекуррентности даёт ${\displaystyle T(n)=1001n^{3}-1000n^{2}}$, при условии ${\displaystyle T(1)=1}$.)

Вариант 2

Общая форма

Если для некоторой константы ${\displaystyle k\geqslant 0}$ выполняется

${\displaystyle f(n)=\Theta (n^{c}\log ^{k}n)}$, где ${\displaystyle c=\log _{b}a}$.

Тогда

${\displaystyle T(n)=\Theta (n^{c}\log ^{k+1}n).}$

Пример

${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+10n.}$

Согласно формуле, значения констант и сложности не рекурсивной части задачи:

${\displaystyle a=2,\ b=2,\ c=1,\ f(n)=10n,}$

${\displaystyle f(n)=\Theta (n^{c}\log ^{k}n)}$, где ${\displaystyle c=1,\ k=0}$.

Проверяем соотношение варианта 2:

${\displaystyle \log _{b}a=\log _{2}2=1}$, и следовательно, ${\displaystyle c=\log _{b}a}$.

В соответствии с 2-м вариантом основной теоремы,

${\displaystyle T(n)=\Theta \left(n^{\log _{b}a}\log ^{k+1}n\right)=\Theta (n^{1}\log ^{1}n)=\Theta (n\log n).}$

Таким образом, рекуррентное соотношение T(n) равно Θ(n log n).

(Этот результат может быть проверен точным решением соотношения, в котором ${\displaystyle T(n)=n+10n\log _{2}n}$, при условии ${\displaystyle T(1)=1}$.)

Вариант 3

Общая форма

Если выполняется

${\displaystyle f(n)=\Omega (n^{c})}$, где ${\displaystyle c>\log _{b}a}$,

а также верно, что

${\displaystyle af\left({\frac {n}{b}}\right)\leqslant kf(n)}$ для некоторой константы ${\displaystyle k<1}$ и достаточно больших ${\displaystyle n}$ (так называемое условие регулярности), тогда

${\displaystyle T(n)=\Theta {\big (}f(n){\big )}.}$

Пример

${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+n^{2}.}$

Значения констант и функции:

${\displaystyle a=2,\ b=2,\ f(n)=n^{2},}$

${\displaystyle f(n)=\Omega (n^{c})}$, где ${\displaystyle c=2}$.

Проверяем, что выполняется соотношение из варианта 3:

${\displaystyle \log _{b}a=\log _{2}2=1}$, и, следовательно, ${\displaystyle c>\log _{b}a}$.

Также выполняется условие регулярности:

${\displaystyle 2\left({\frac {n^{2}}{4}}\right)\leqslant kn^{2}}$ при выборе ${\displaystyle k=1/2}$.

Следовательно, согласно 3-му варианту основной теоремы,

${\displaystyle T(n)=\Theta {\big (}f(n){\big )}=\Theta (n^{2}).}$

Данное рекуррентное соотношение T(n) равно Θ(n²), что совпадает с f(n) в изначальной формуле.

(Этот результат подтверждается точным решением рекуррентности, в котором ${\displaystyle T(n)=2n^{2}-n}$, при условии ${\displaystyle T(1)=1}$.)

Выражения, не решаемые основной теоремой

Следующие соотношения не могут быть решены с применением основной теоремы:^[2]

• ${\displaystyle T(n)=2^{n}T\left({\frac {n}{2}}\right)+n^{n}.}$

  a не является константой, для основной теоремы требуется постоянное количество подзадач.

• ${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+{\frac {n}{\log n}}.}$

  Между f(n) и ${\displaystyle n^{\log _{b}a}}$ существует неполиномиальная зависимость.

• ${\displaystyle T(n)=0{,}5T\left({\frac {n}{2}}\right)+n.}$

  a < 1, но основная теорема требует наличия хотя бы одной подзадачи.

• ${\displaystyle T(n)=64T\left({\frac {n}{8}}\right)-n^{2}\log n.}$

  f(n) является отрицательной величиной.

• ${\displaystyle T(n)=T\left({\frac {n}{2}}\right)+n(2-\cos n).}$

  Близко к варианту 3, но не выполняется условие регулярности.

Во втором примере разница между ${\displaystyle f(n)}$ и ${\displaystyle n^{\log _{b}a}}$ может быть выражена соотношением ${\displaystyle {\frac {f(n)}{n^{\log _{b}a}}}={\frac {\frac {n}{\log n}}{n^{\log _{2}2}}}={\frac {n}{n\log n}}={\frac {1}{\log n}}.}$ Из него видно, что ${\displaystyle {\frac {1}{\log n}}<n^{\varepsilon }}$ для любой константы ${\displaystyle \varepsilon >0}$. Следовательно, разница не является полиномом, и основная теорема неприменима.

Применение к некоторым алгоритмам

Алгоритм	Рекуррентное соотношение	Время работы	Примечание
Двоичный поиск	${\displaystyle T(n)=T\left({\frac {n}{2}}\right)+O(1)}$	${\displaystyle O(\log n)}$	Основная теорема, 2 вариант: ${\displaystyle c=\log _{b}a}$, где ${\displaystyle a=1,b=2,c=0,k=0}$[3]
Обход двоичного дерева	${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+O(1)}$	${\displaystyle O(n)}$	Основная теорема, 1 вариант: ${\displaystyle c<\log _{b}a}$ где ${\displaystyle a=2,b=2,c=0}$[3]
Алгоритм Штрассена	${\displaystyle T(n)=7T\left({\frac {n}{2}}\right)+O(n^{2})}$	${\displaystyle O(n^{\log _{2}7})\approx O(n^{2{,}81})}$	Основная теорема, 1 вариант: ${\displaystyle c<\log _{b}a}$, где ${\displaystyle a=7,b=2,c=2}$[4]
Optimal sorted matrix search	${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+O(\log n)}$	${\displaystyle O(n)}$	Теорема Akra — Bazzi для ${\displaystyle p=1}$ и ${\displaystyle g(u)=\log(u)}$ для получения ${\displaystyle \Theta (2n-\log n)}$
Сортировка слиянием	${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+O(n)}$	${\displaystyle O(n\log n)}$	Основная теорема, 2 вариант: ${\displaystyle c=\log _{b}a}$, где ${\displaystyle a=2,b=2,c=1,k=0}$

См. также

• Akra–Bazzi method

Примечания

Литература

• Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4. Главы 4.3 (основная теорема) и 4.4 (доказательство)
  • Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford. Introduction to Algorithms. — 2nd. — MIT Press and McGraw-Hill, 2001. — ISBN 0-262-53196-8. Sections 4.3 (The master method) and 4.4 (Proof of the master theorem), pp. 73-90. (англ.)
• Michael T. Goodrich and Roberto Tamassia. Algorithm Design: Foundation, Analysis, and Internet Examples. Wiley, 2002. ISBN 0-471-38365-1. The master theorem (including the version of Case 2 included here, which is stronger than the one from CLRS) is on pp. 268—270. (англ.)
• CHAPTER 5. RECURSION AND RECURRENCES 5.2 The Master Theorem Архивная копия от 21 апреля 2017 на Wayback Machine, CS 21/Math 19 — Course Notes Архивная копия от 21 июля 2010 на Wayback Machine, Ken Bogart and Cliff Stein: Discrete Math in Computer Science.

Эта страница в последний раз была отредактирована 4 марта 2023 в 01:12.