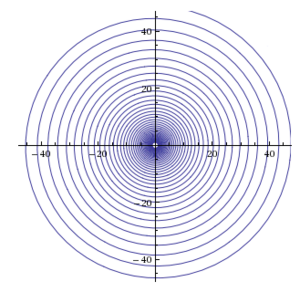
Логарифмическая спираль

Логарифми́ческая спира́ль или изогональная спираль — особый вид спирали, часто встречающийся в природе.

История

Логарифмическая спираль была впервые описана Декартом и позже интенсивно исследована Бернулли, который называл её Spira mirabilis — «удивительная спираль». Декарт искал кривую, обладающую свойством, подобным свойству окружности, так чтобы касательная в каждой точке образовывала с радиус-вектором в каждой точке один и тот же угол. Он показал, что это условие равносильно тому, что полярные углы для точек кривой пропорциональны логарифмам радиус-векторов.

Уравнения

В полярных координатах кривая может быть записана как

${\displaystyle r=ae^{b\theta }}$

или соответственно

${\displaystyle \theta ={\frac {1}{b}}\ln(r/a),}$

где ${\displaystyle \theta }$ — угол отклонения точки от нуля, r — радиус-вектор точки, a — коэффициент, отвечающий за радиус витков, b — коэффициент, отвечающий за расстояние между витками, e — число Эйлера.

В параметрической форме может быть записана как

${\displaystyle x(t)=r\cos t=ae^{bt}\cos t\,,}$

${\displaystyle y(t)=r\sin t=ae^{bt}\sin t\,,}$

где a, b — действительные числа, t — аналог ${\displaystyle \theta }$ в выражении в полярных координатах

Свойства

• Угол, составляемый касательной в произвольной точке логарифмической спирали с радиус-вектором точки касания, постоянный и зависит лишь от параметра b. В терминах дифференциальной геометрии это может быть записано как

${\displaystyle {\dfrac {\langle \mathbf {r} (\theta ),\mathbf {r} '(\theta )\rangle }{\|\mathbf {r} (\theta )\|\|\mathbf {r} '(\theta )\|}}={\dfrac {b}{\sqrt {1+b^{2}}}}=\cos \varphi ;\quad b=\mathrm {ctg} \,\varphi .}$

• Производная функции ${\displaystyle \mathbf {r} '(\vartheta )}$ пропорциональна параметру b. Другими словами, он определяет, насколько плотно и в каком направлении закручивается спираль. В предельном случае, когда b = 0 ${\displaystyle (\varphi =\pi /2)}$ спираль вырождается в окружность радиуса a. Наоборот, когда b стремится к бесконечности ${\displaystyle (\varphi \rightarrow 0),}$ спираль стремится к прямой линии. Угол, дополняющий ${\displaystyle \varphi }$ до 90°, называется наклоном спирали.
• Каждый следующий виток подобен предыдущему. Другими словами, размер витков логарифмической спирали постепенно увеличивается, но их форма остаётся неизменной.
• Прирост радиуса на единицу длины окружности постоянен. Возможно, в результате этого свойства логарифмическая спираль появляется в определённых растущих формах, подобных раковинам моллюсков, шляпкам подсолнечников, спиралям циклонов и галактик.
• Если угол ${\displaystyle \theta }$ возрастает или убывает в арифметической прогрессии, то r возрастает (убывает) в геометрической.
• Поворачивая полярную ось вокруг полюса, можно добиться полного уничтожения параметра a и привести уравнение к виду ${\displaystyle r=e^{m\theta }}$, где m  — новый параметр.
• Радиус кривизны в каждой точке спирали пропорционален длине дуги спирали от её начала до этой точки.

Интересные факты

• Якоб Бернулли хотел, чтобы на его могиле была выгравирована логарифмическая спираль, но вместо этого по ошибке на его надгробие поместили архимедову спираль. Тем не менее, надпись на латыни, выгравированная согласно завещанию вокруг спирали, «EADEM MUTATA RESURGO» («изменённая, я вновь воскресаю»), свидетельствует о том, что имеется в виду именно логарифмическая спираль, которая обладает замечательным свойством восстанавливать свою форму после различных преобразований.
• В репертуаре группы Tool композиция Lateralus посвящена спиралям.

• 
  a=0.01, b=0.15
• 
  a=1, b=0.15
• 
  a=1000, b=0.15
• 
  Раковина моллюска по форме близка к логарифмической спирали
• 
  Область низкого давления над Исландией
• 
  Спиральная галактика Водоворот

Обобщение

Логарифмическая спираль есть Синусоидальная спираль при ${\displaystyle n\to 1}$;

См. также

• Золотая спираль

Ссылки

• На Викискладе есть медиафайлы по теме Логарифмическая спираль

Эта страница в последний раз была отредактирована 16 февраля 2024 в 06:23.