Las transformaciones isométricas son transformaciones de figuras en el plano que se realizan sin variar las dimensiones ni el área; la figura inicial y la final son semejantes, y geométricamente congruentes.
La palabra isometría tiene su origen en el griego iso (igual o mismo) y metria (medir), una definición cercana es igual medida. Existen tres tipos de isometrías: traslación, simetría y rotación.
YouTube Encyclopedic
-
1/3Views:133 7423 71440 201
-
Transformaciones isométricas 01: Traslación, Simetria, Rotación
-
Matemática - Isometrías
-
PSU:Transformaciones isométricas. Clase 1 - Profesor Danny Perich
Transcription
Discusión informal
Informalmente, las isometrías en el plano euclidiano son una manera de transformar al plano sin “deformarlo”, manteniendo las distancias. Si se piensa en el plano euclidiano como una hoja de plástico transparente sobre una mesa, las distintas isometrías se verían como:
- Desplazar la hoja diez centímetros a la derecha. (Traslación)
- Rotar la hoja diez grados en sentido de las manecillas del reloj alrededor de un punto fijo. (Rotación)
- Voltear la hoja como para ver su reverso. (Simetría o reflexión)
A veces, también se menciona a la reflexión con desplazamiento (que equivale a una reflexión y una traslación) como una isometría. En el ejemplo previo se podría ver como voltear la hoja y desplazarla 5 centímetros a la derecha.
De hecho, cualquier composición de las isometrías anteriores también sería una simetría dado que las dimensiones y el área se mantienen en cada transformación.
Sin embargo, doblar, cortar o derretir la hoja de plástico no son consideradas isometrías. Tampoco lo son estirar o encoger la hoja, pues las dimensiones (o distancias) no se conservarían tras dichas transformaciones.
Definición formal
Una isometría en el plano euclidiano es una transformación que preserva distancias en el plano. Es un mapeo
de tal suerte que para cualesquiera puntos p y q en el plano,
donde d(p, q) es la distancia euclidiana entre p y q.
Traslación
La traslación es una isometría que realiza un cambio de posición o lugar en el espacio, manteniendo las direcciones (medidas angulares y longitudinales) de todos los elementos del espacio, dicha traslación puede ser determinadas por un vector o por dos puntos (el origen y el destino).
 |
 |
Simetría
Simetría es la correspondencia exacta en la disposición regular de las partes o puntos de un cuerpo o figura con relación a un punto (centro), una recta (eje) o un plano. Se denominan: central, axial y especular o bilateral.
Simetría central
La simetría central, en geometría, es una transformación en la que a cada punto se le asocia otro punto, que debe cumplir las siguientes condiciones:
a) El punto y su imagen estén a igual distancia de un punto llamado centro de simetría.
b) El punto, su imagen y el centro de simetría pertenezcan a una misma recta.
 |
 |
Simetría axial
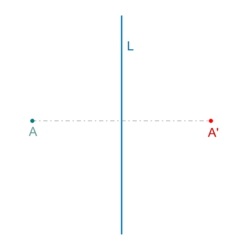
La simetría axial, en geometría, es una transformación respecto de un eje de simetría, en la cual, a cada punto de una figura se asocia a otro punto llamado imagen, que cumple con las siguientes condiciones:
a) La distancia de un punto y su imagen al eje de simetría, es la misma.
b) El segmento que une un punto con su imagen, es perpendicular al eje de simetría.
 |
 |
En la simetría axial se conservan las distancias pero no la dirección de los ángulos. El eje de simetría es la mediatriz del segmento AA'.
Composición de simetrías
Si se aplica la misma simetría dos veces, se obtiene una identidad.
Si se aplican dos simetrías respecto de ejes paralelos, se obtiene una traslación cuyo desplazamiento es el doble de la distancia entre dichos ejes.
Si se aplican dos simetrías respecto de ejes que se cortan en O, se obtiene giro con centro en O, cuyo ángulo es el doble del que forman dichos ejes.
Rotación
Una rotación, en geometría, es un movimiento de cambio de orientación de un cuerpo, de forma que, dado un punto cualquiera del mismo, este permanece a una distancia constante de un punto fijo, y tiene las siguientes características:
- Un punto denominado centro de rotación.
- Un ángulo
- Un sentido de rotación.
Estas transformaciones pueden ser positivas o negativas dependiendo del sentido de giro. Para el primer caso debe ser un giro en sentido contrario a las manecillas del reloj, y será negativo el giro cuando sea en sentido de las manecillas.


