El radián (símbolo: ) es una unidad de la amplitud de ángulos. El radián mide el ángulo presentado como central a una circunferencia y su medida es igual a la razón entre la longitud del arco que comprende de dicha circunferencia y la longitud del radio, es decir, mide la cantidad de veces que la longitud del radio traza ese determinado arco en la circunferencia. Hasta 1995 tuvo la categoría de unidad suplementaria en el Sistema Internacional de Unidades, junto con el estereorradián.[1] A partir de ese año, y hasta el momento presente, ambas unidades figuran en la categoría de unidades derivadas. El radián se define en el SI como una unidad adimensional con 1 = 1.[2]
Esta unidad se utiliza primordialmente en física, cálculo infinitesimal, trigonometría, goniometría, etc.

YouTube Encyclopedic
-
1/3Views:24 56026 0785 547
-
Qué es un Radián
-
Radián definición
-
A radián bevezetése
Transcription
Definición
Un radián es la unidad de medida de un ángulo con vértice en el centro de un círculo cuyos lados son cortados por el arco de la circunferencia, y que además dicho arco tiene una longitud igual a la del radio.[3][4]
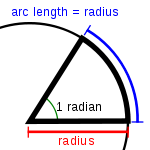
El ángulo formado por dos radios de una circunferencia, medido en radianes, es igual a la longitud del arco que delimitan los radios dividida entre el radio; es decir, θ = s/r, donde θ es el ángulo, s es la longitud de arco, y r es el radio. Por tanto, el ángulo completo, , que subtiende una circunferencia de radio r, medido en radianes, es:
De forma más general, la magnitud en radianes de un ángulo subtendido es igual al cociente entre la longitud del arco y el radio del círculo; es decir, , donde θ es el ángulo subtendido en radianes, s es la longitud del arco y r es el radio. Un ángulo recto es exactamente radianes.[5]
El ángulo de rotación (360°) correspondiente a una revolución completa es la longitud de la circunferencia dividida por el radio, que es , o 2π. Por lo tanto, 2π radianes es igual a 360 grados.
La relación 2π rad = 360° se puede derivar usando la fórmula para longitud de arco, . Dado que el radián es la medida de un ángulo subtendido por un arco de longitud igual al radio de la circunferencia, . Esto se puede simplificar aún más a . Multiplicando ambos lados por 360° se obtiene 360° = 2π rad.
Utilidad
El radián es una unidad sumamente útil para medir ángulos, puesto que simplifica los cálculos, ya que los más comunes se expresan mediante sencillos múltiplos o divisores de π.
Símbolo de la unidad
La Oficina Internacional de Pesas y Medidas[6] y la Organización Internacional de Normalización[7] especifican rad como símbolo del radián. Símbolos alternativos que estaban en uso en 1909 son c (la letra c en superíndice, por "medida circular"), la letra r, o un superíndice R,[8] pero estas variantes se utilizan con poca frecuencia, ya que pueden confundirse con un símbolo de grado (°) o un radio (r). Así, un ángulo de 1,2 radianes se escribiría hoy como 1,2 rad; las notaciones arcaicas podrían incluir 1,2 r, 1,2rad, 1,2c, o 1,2R.
En la escritura matemática, a menudo se omite el símbolo "rad". Cuando se cuantifica un ángulo en ausencia de cualquier símbolo, se asumen los radianes, y cuando se quiere decir grados, se utiliza el símbolo de grado. °.
Análisis dimensional
El radián es la unidad natural en la medida de los ángulos. Por ejemplo, la función seno de un ángulo x expresado en radianes cumple:
Análogamente los desarrollos Taylor de las funciones seno y coseno son:
donde x se expresa en radianes.
El ángulo plano se define como θ = s/r}, donde θ es el ángulo subtendido en radianes, s es la longitud del arco, y r es el radio. Un radián corresponde al ángulo para el que s = r}, por tanto 1 radián = 1 m/m.[9] Sin embargo, rad sólo debe utilizarse para expresar ángulos, no para expresar relaciones de longitudes en general.[6]. Un cálculo similar utilizando el área de un sector circular θ = 2A/r2 da 1 radián como 1 m2/m2.[10] El hecho clave es que el radián es una unidad adimensional igual a 1. En el SI 2019, el radián se define en consecuencia como 1 rad = 1.[11] Es una práctica establecida desde hace mucho tiempo en matemáticas y en todas las áreas de la ciencia hacer uso de rad = 1. [12][13] En 1993 la American Association of Physics Teachers Metric Committee especificó que el radián debía aparecer explícitamente en las cantidades sólo cuando se obtuvieran valores numéricos diferentes al utilizar otras medidas angulares, como en las cantidades de dida angular (rad), velocidad angular (rad/s), aceleración angular (rad/s2), y rigidez de torsión (N⋅m/rad), y no en las cantidades de par de torsión (N⋅m) y momento angular (kg⋅m2/s). [14]
Giacomo Prando afirma que "el estado actual de las cosas conduce inevitablemente a apariciones y desapariciones fantasmales del radián en el análisis dimensional de las ecuaciones físicas".[15] Por ejemplo, un objeto colgado de una cuerda de una polea subirá o bajará y = rθ centímetros, donde r es el radio de la polea en centímetros y θ es el ángulo que gira la polea en radianes. Al multiplicar r por θ la unidad de radianes desaparece del resultado. Del mismo modo, en la fórmula para la velocidad angular de una rueda rodante, ω = v/r}, los radianes aparecen en las unidades de ω pero no en el lado derecho.[16] Anthony French llama a este fenómeno "un problema perenne en la enseñanza de la mecánica".[17] Oberhofer dice que el consejo típico de ignorar los radianes durante el análisis dimensional y añadir o quitar radianes en las unidades según la convención y el conocimiento contextual es "pedagógicamente insatisfactorio".[18]
Al menos una docena de científicos entre 1936 y 2022 han hecho propuestas para tratar el radián como una unidad de medida base que define su propia dimensión de "ángulo". [19][20][21] La revisión de propuestas de Quincey esboza dos clases de propuestas. La primera opción cambia la unidad de un radio a metros por radián, pero esto es incompatible con el análisis dimensional para el área del círculo, πr2. La otra opción es introducir una constante dimensional. Según Quincey, este enfoque es "lógicamente riguroso" en comparación con el SI, pero requiere "la modificación de muchas ecuaciones matemáticas y físicas familiares".[22]
En particular, Quincey identifica la propuesta de Torrens de introducir una constante η igual a 1 radián inverso (1 rad-1) de forma similar a la introducción de una constante ε0. [22][23] Con este cambio, la fórmula para el ángulo subtendido en el centro de un círculo, s = rθ, se modifica para convertirse en s = ηrθ, y la serie de Taylor para el seno de un ángulo θ pasa a ser: [21][24]
El SI puede considerarse en relación con este marco como un sistema de unidades naturales en el que se supone que se cumple la ecuación η = 1, o de forma similar, 1 rad = 1. Esta convención del radián permite omitir η en las fórmulas matemáticas.[27]
Una constante dimensional para el ángulo es "bastante extraña" y es probable que la dificultad de modificar las ecuaciones para añadir la constante dimensional impida su uso generalizado.[21] Definir el radián como unidad base puede ser útil para el software, donde la desventaja de ecuaciones más largas es mínima. [28] Por ejemplo, la biblioteca de unidades Boost define unidades angulares con una dimensión ángulo_plano,[29] y el sistema de unidades de Mathematica considera de forma similar que los ángulos tienen una dimensión angular. [30][31]
Equivalencias
- La equivalencia entre grados sexagesimales y radianes es: π rad = 180°. Por tanto
1 radián = 57,29577951… grados sexagesimales y
1 grado sexagesimal = 0,01745329252… radianes.
- La equivalencia entre grados centesimales y radianes es: π rad = 200g
La tabla muestra la conversión de los ángulos más comunes.
| Grados | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| Radianes | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 7π/6 | 5π/4 | 4π/3 | 3π/2 | 5π/3 | 7π/4 | 11π/6 | 2π |
Otras unidades de medida de ángulos convencionales son el grado sexagesimal, el grado centesimal y, en astronomía, la hora.
- El radián tiene una unidad derivada llamada radián por segundo (rad/s), que corresponde a la magnitud velocidad angular. Esta unidad tiene una equivalencia con las rpm. Las equivalencias se pueden calcular fácilmente haciendo la siguiente relación:
, que simplificada es: , o bien: .
Es decir que, para pasar una cantidad x de rpm a rad/s tenemos que multiplicarla por π/30:
Análogamente, para pasar una cantidad y de rad/s a rpm tenemos que multiplicarla por 30/π:
Conversiones entre grados y radianes
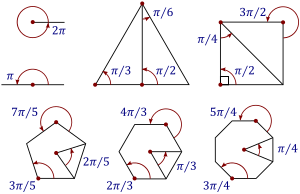

Los grados y los radianes son dos diferentes sistemas para medir ángulos. Un ángulo de ° equivale a radianes; un ángulo de ° equivale a radianes; y un ángulo de ° equivale a .
Convertir grados a radianes
Lo primero que tenemos que hacer para convertir ° a radianes es buscar ° (un grado). Sabiendo que ° = simplemente dividimos por :
Entonces nos quedaría:
Y ahora multiplicamos por :
Entonces queda resolver el lado derecho de la ecuación:
Ya en este punto, multiplicamos fracciones:
Y ya tendríamos el resultado:
Convertir de radianes a grados
Para convertir de radianes a grados, simplemente partimos de que radián es igual a , entonces, multiplicamos la medida dada en radianes por :
Entonces tenemos que el resultado es
Diferencia entre radián, gradián, y grado sexagesimal
Los tres son unidades de medida de ángulos planos, y se diferencian así:
- Radián (rad): ángulo que describe un arco cuya longitud es la del radio.
- Gradián o grado centesimal (g): ángulo que describe un arco cuya longitud es la cuadringentésima (1/400) parte de una circunferencia.
- Grado sexagesimal (°): ángulo que describe un arco cuya longitud es la tricentésima sexagésima (1/360) parte de una circunferencia.
Conversión de ángulos comunes
| Unidades | Valores | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Revolución | 0 | 172 | 112 | 18 | 16 | 14 | 12 | 34 | 1 |
| Grados (sexagesimales) | 0° | 5° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Radianes | 0 rad | π36 rad | π6 rad | π4 rad | π3 rad | π2 rad | π rad | 3π2 rad | 2π rad |
| 𝜏72 rad | 𝜏12 rad | 𝜏8 rad | 𝜏6 rad | 𝜏4 rad | 𝜏2 rad | 3𝜏4 rad | 𝜏 rad | ||
| Gradianes (grados centesimales) | 0g | 50g9 | 100g3 | 50g | 200g3 | 100g | 200g | 300g | 400g |
Véase también
Referencias
- ↑ «Resolution 8 of the CGPM at its 20th Meeting (1995)». Bureau International des Poids et Mesures. Archivado desde el original el 25 de diciembre de 2018. Consultado el 23 de septiembre de 2014.
- ↑ International Bureau of Weights and Measures, 2019, p. 151: "The CGPM decided to interpret the supplementary units in the SI, namely the radian and the steradian, as dimensionless derived units."
- ↑ «¿Qué es un radián?». 30 de octubre de 2014. Consultado el 29 de julco=Gaussianos.
- ↑ Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd edición), Reading: Addison-Wesley, p. APP-4, LCCN 76087042.
- ↑ International Bureau of Weights and Measures, 2019, p. 151.
- ↑ a b Oficina Internacional de Pesas y Medidas, 2019, p. 151.
- ↑ «ISO 80000-3:2006 Cantidades y unidades - Espacio y tiempo». 17 de enero de 2017.
- ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasHall_1909 - ↑ Oficina Internacional de Pesas y Medidas, 2019, p. 151: "Un radián corresponde al ángulo para el que s = r"
- ↑ Quincey, 2016, p. 844: "También, como se alude en Mohr y Phillips, 2015, el radián puede definirse en términos del área A de un sector (A = 12 θ r2), en cuyo caso tiene las unidades m2⋅m-2. "
- ↑ Oficina Internacional de Pesas y Medidas, 2019, p. 151: "Un radián corresponde al ángulo para el cual s = r}, por lo tanto 1 rad = 1."
- ↑ Oficina Internacional de Pesas y Medidas, 2019, p. 137.
- ↑ Bridgman, Percy Williams (1922). org/details/dimensionalanaly00bridrich/page/n13/mode/2up Análisis dimensional. New Haven : Yale University Press. «Amplitud angular de oscilación [...] Sin dimensiones.»
- ↑ Aubrecht, Gordon J.; French, Anthony P.; Iona, Mario; Welch, Daniel W. (February 1993). «El radián-La unidad problemática». The Physics Teacher 31 (2): 84-87. Bibcode:1993PhTea..31...84A. doi:10.1119/1.2343667.
- ↑ Prando, Giacomo (August 2020). «Una unidad espectral». Nature Physics 16 (8): 888. Bibcode:.16..888P 2020NatPh. .16..888P. S2CID 225445454. doi:10.1038/s41567-020-0997-3. Parámetro desconocido
|doi-access=ignorado (ayuda) - ↑ Leonard, William J. (1999). Minds-on Physics: Advanced topics in mechanics (en inglés). Kendall Hunt. p. 262. ISBN 978-0-7872-5412-4.
- ↑ French, Anthony P. (Mayo 1992). «¿Qué pasa con los 'radianes'? (comentario)». The Physics Teacher 30 (5): 260-261.
- ↑ Oberhofer, E. S. (Marzo 1992). «¿Qué pasa con los 'radianes'?». The Physics Teacher 30 (3): 170-171. Bibcode:1992PhTea..30..170O.
- ↑ Brinsmade, 1936; Romain, 1962; Eder, 1982; Torrens, 1986; Brownstein, 1997; Lévy-Leblond, 1998; Foster, 2010; Mills, 2016; Quincey, 2021; Leonard, 2021; Mohr et al., 2022
- ↑ Mohr y Phillips, 2015.
- ↑ a b c d Quincey, Paul; Brown, Richard J C (1 de junio de 2016). «Implicaciones de la adopción del ángulo plano como magnitud base en el SI». Metrologia 53 (3): 998-1002. Bibcode:2016Metro..53..998Q. S2CID 119294905. arXiv:02373 1604. 02373. doi:10.1088/0026-1394/53/3/998.
- ↑ a b Quincey, 2016.
- ↑ Otras propuestas incluyen la abreviatura "rad" (Brinsmade, 1936), la notación (Romain, 1962), y las constantes ם (Brownstein, 1997), ◁ (Lévy-Leblond, 1998), k (Foster, 2010), θC (Quincey, 2021), y (et al., Trott).
- ↑ a b Torrens, 1986.
- ↑ Mohr et al., 2022, p. 6.
- ↑ Mohr et al., 2022, pp. 8-9.
- ↑ Quincey, 2021.
- ↑ Quincey, Paul; Brown, Richard J C (1 de agosto de 2017). «Un enfoque más claro para definir sistemas de unidades». Metrologia 54 (4): 454-460. Bibcode:.54..454Q 2017Metro. .54..454Q. S2CID 119418270. arXiv:1705.03765. doi:10.1088/1681-7575/aa7160.
- ↑ Schabel, Matthias C.; Watanabe, Steven. «Boost.Units FAQ - 1.79.0». www.boost.org. Consultado el 5 de mayo de 2022. «Los ángulos se tratan como unidades».
- ↑ Mohr et al., 2022, p. 3.
- ↑ «DimensionesUnitarias-Documentación del Lenguaje Wolfram». reference.wolfram.com. Consultado el 1 de julio de 2022.
Bibliografía
- Florian Cajori, 1929, History of Mathematical Notations, Vol. 2, pp. 147–148; Nature, 1910, Vol. 83, pp. 156, 217, y 459—460;












































