Una operación bit a bit o bitwise opera sobre números binarios a nivel de sus bits individuales. Es una acción primitiva rápida, soportada directamente por los procesadores. En procesadores simples de bajo costo, las operaciones de bit a bit, junto con los de adición y sustracción, son típicamente sustancialmente más rápidas que la multiplicación y la división, mientras que en los modernos procesadores de alto rendimiento usualmente las operaciones se realizan casi a la misma velocidad.
YouTube Encyclopedic
-
1/5Views:21 5031 1513 7631 015601
-
Curso de C - Operadores a nivel de bit
-
Operador bit a bit OR | | UPV
-
Operador Bit a Bit AND | | UPV
-
Consulta de estado de un bit con el operador bit a bit AND | | UPV
-
Operador Bit a Bit NOT | | UPV
Transcription
Tipos de operaciones
- Operaciones bit a bit: Ejecutan las operaciones lógicas AND, OR, XOR, NOT, etc, sobre los bits individuales de los operandos.
- Operaciones de desplazamiento: Desplazan los bits de los operandos hacia la derecha o hacia la izquierda una o más posiciones.
- Operaciones de rotación: Rotan los bits del operando hacia la derecha o hacia la izquierda una o más posiciones. Pueden usar o no el flag del acarreo como un bit adicional en la rotación.
Operadores bit a bit
En las explicaciones de abajo, cualquier indicación de una posición de un bit es contada de derecha a izquierda a partir del bit menos significativo. Por ejemplo, el valor binario 0001 (el decimal 1) tiene ceros en cada posición excepto en la primera.
NOT
| A | NOT A |
| 0 | 1 |
| 1 | 0 |
El NOT bit a bit, o bitwise, o complemento, es una operación unaria que realiza la negación lógica en cada bit, invirtiendo los bits del número, de tal manera que los ceros se convierten en 1 y viceversa. Por ejemplo:
NOT 10011 = 01100
- El NOT forma el complemento a uno de un valor binario dado.
- En un número entero con signo en complemento a dos, el NOT da como resultado el inverso aditivo del número menos 1, es decir
NOT x = -x - 1. Para obtener el complemento a dos de un número, se debe sumar 1 al resultado, dando el negativo del número. Esto equivale a un cambio de signo del número: +5 se convierte en -5, y -5 se convierte en +5. - Para los enteros sin signo, el complemento bit a bit es la “reflexión de espejo” del número a través del punto medio del rango del entero. Por ejemplo, para los enteros sin signo de 8 bits,
NOT x = 255 - x, para los enteros sin signo de 16 bits,NOT x = 65535 - x, y en general, para los enteros sin signo de n bits,NOT x = (2n - 1) - x.
AND
| A | B | A AND B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
El AND bit a bit, o bitwise, toma dos números enteros y realiza la operación AND lógica en cada par correspondiente de bits. El resultado en cada posición es 1 si el bit correspondiente de los dos operandos es 1, y 0 de lo contrario, por ejemplo:
0101 AND 0011 = 0001
El AND puede ser usado para filtrar determinados bits, permitiendo que unos bits pasen y los otros no. También puede usarse en sistemas de mayor fiabilidad.
Determinando el estado de bits
El AND puede ser usado para determinar si un bit particular está encendido (1) o apagado (0). Por ejemplo, dado un patrón de bits 0011, para determinar si el segundo bit está encendido se usa una operación AND con una máscara que contiene encendido solo el segundo bit, que es el que se quiere determinar:
0011 AND 0010 (máscara) = 0010
Puesto que el resultado 0010 es diferente de cero, se sabe que el segundo bit en el patrón original está encendido. Esto es a menudo llamado enmascaramiento del bit (bit masking). (Por analogía, al uso de las cintas de enmascarar, que cubren o enmascaran porciones que no deben ser alteradas o porciones que no son de interés. En este caso, los valores 0 enmascaran los bits que no son de interés).
Extrayendo bits
El AND se puede usar para extraer determinados bits de un valor. Si en un byte, por ejemplo, tenemos representados dos dígitos hexadecimales empaquetados, (uno en los 4 bits superiores y el otro en los 4 bits inferiores), podemos extraer cada dígito hexadecimal usando el AND con las máscaras adecuadas:
0011 0101 0011 0101 AND 1111 0000 (máscara) AND 0000 1111 (máscara) = 0011 0000 = 0000 0101 Hex. superior Hex. inferior
Apagando bits
El AND también se puede usar para apagar determinados bits. Solo hay que poner una máscara con bits en cero en las posiciones de los bits que se quieren apagar y 1 en los demás bits. Todos los demás bits con la máscara 1 pasarán inalterados, y los que tienen la máscara 0 se apagarán. Dado el ejemplo 0111, el segundo bit puede ser apagado usando un AND con el patrón que tiene un cero en el segundo bit y un 1 en el resto de los bits:
0111 AND 1101 (máscara) = 0101
OR
| A | B | A OR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Una operación OR de bit a bit, o bitwise, toma dos números enteros y realiza la operación OR inclusivo en cada par correspondiente de bits. El resultado en cada posición es 1 si el bit correspondiente de cualquiera de los dos operandos es 1, y 0 si ambos bits son 0, por ejemplo:
0101 OR 0011 = 0111
Encendiendo bits
El OR bit a bit, o bitwise, puede ser usado para encender un bit individual o un conjunto de bits. Para ello se usa una máscara OR con los bits que se quieren encender en 1 y el resto de los bits en cero. El resultado será que todos los bits originales quedarán como estaban excepto los bits en donde la máscara tenga 1, que resultarán encendidos. Por ejemplo, si en el patrón de bits 0101 se quiere encender el segundo bit se hará de la manera siguiente:
0101 OR 0010 (máscara) = 0111
Copiando bits
El OR, y el desplazamiento lógico (explicado más adelante), puede ser usado para copiar un grupo de bits a una posición determinada.
Supongamos que tenemos el signo, el exponente, y la parte significativa de un número, en diferentes registros de 32 bits, y queremos empaquetarlos para formar un número en representación de punto flotante de simple precisión de 32 bits:
Signo: 00000000000000000000000000000001 Exponente: 00000000000000000000000010000011 Parte significativa: 00000000011100000111000000001110
Todos ellos tienen los valores correctos y tenemos que mover cada uno de ellos a su posición para poder armar el punto flotante.
Se debe mover el signo 31 posiciones hacia la izquierda, el exponente 23 posiciones hacia la izquierda, y la parte significativa no es necesaria moverla porque ya está en la posición correcta. Estos desplazamientos se hacen con la operación de desplazamiento hacia la izquierda descrito más adelante:
Signo: 10000000000000000000000000000000 <-- Se desplaza el signo 31 posiciones hacia la izquierda Exponente: 01000001100000000000000000000000 <-- Se desplaza el exponente 23 posiciones hacia la izquierda Parte significativa: 00000000011100000111000000001110 <-- La parte significativa no se mueve, ya está en su lugar
Ahora que tenemos cada parte del número en su lugar, las combinamos para empaquetarlas y formar el número en su representación de punto flotante de 32 bits. Para ello usamos el OR: (Resultado final) = (Signo) OR (Exponente) OR (Parte significativa):
Signo: 10000000000000000000000000000000 Exponente: 01000001100000000000000000000000 Parte significativa: 00000000011100000111000000001110 Resultado final: 11000001111100000111000000001110
Ya tenemos el número en su representación de punto flotante definitiva.
Procedimiento genérico para copiar un grupo de bits
Para copiar una serie de bits en un lugar determinado usando OR, se necesita que ese lugar donde se van a copiar tenga sus bits en cero (para hacer un espacio libre para poder copiar los bits). También se necesita que el registro donde se encuentran los bits que se quieren copiar tenga los demás bits (los que no se quieren copiar) apagados. Ambas operaciones, aclarar los bits en el lugar del destino, y aclarar los bits que no se quieren copiar se hacen con AND:
Tenemos dos registros de 16 bits:
Registro A: 1011 1100 0110 1100 Registro B: 1001 0001 1111 1010
Queremos copiar los cuatro bits menos significativos del registro A en el registro B.
Para ello, primero aclaramos los 4 bits menos significativos de B con una operación AND, y así tener un espacio libre:
1001 0001 1111 1010 <-- Valor original del registro B
AND 1111 1111 1111 0000 <-- Máscara para aclarar los bits de B donde se van a copiar los que vienen de A
= 1001 0001 1111 0000 <-- Registro B preparado para recibir los 4 bits menos significativos de A
Luego, aclaramos los bits de A que no queremos copiar, dejando solo los bits que queremos copiar:
1011 1100 0110 1100 <-- Valor original del registro A
AND 0000 0000 0000 1111 <-- Máscara para dejar solo los bits de A que se quieren copiar
= 0000 0000 0000 1100 <-- Registro A con solo los bits que se desean copiar
Ahora estamos listos para hacer el OR de A sobre B y combinar los 4 bits menos significativos de A sobre B:
0000 0000 0000 1100 <-- Registro A con los 4 bits que se desean copiar OR 1001 0001 1111 0000 <-- Registro B con un espacio para los 4 bits que desean copiar = 1001 0001 1111 1100 <-- Registro B con los 4 bits menos significativos de A copiados sobre él
Ahora, el registro B tiene copiado los 4 bits menos significativos de A. El resto de los bits de B quedaron intactos.
XOR
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
El XOR bit a bit, o bitwise, toma dos números enteros y realiza la operación OR exclusivo en cada par correspondiente de bits. El resultado en cada posición es 1 si el par de bits son diferentes y cero si el par de bits son iguales. Por ejemplo:
0101 XOR 0011 = 0110
Invirtiendo bits selectivamente
A diferencia del NOT, que invierte todos los bits de un registro, el XOR bit a bit, o bitwise, puede ser usado para invertir selectivamente uno o más bits en un registro. Dado el patrón de bits 0011, el segundo y el cuarto bit pueden ser invertidos por XOR con una máscara con un patrón de bits conteniendo 1 en las posiciones que se quieren invertir, la segunda y cuarta, y 0 en las demás. Los bits de las posiciones con cero de la máscara resultarán inalterados:
0011 XOR 1010 (máscara) = 1001
Igualdad y desigualdad de bits
XOR es equivalente y tiene la misma tabla de verdad que la desigualdad, XOR y desigualdad son sinónimos:
| A | B | A XOR B | A <> B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
El XOR puede usarse para saber si los bits correspondientes de dos operandos son iguales o diferentes. Por ejemplo, si tenemos dos operandos, 1000 y 0010 y queremos saber si los bits más significativos de ambos son iguales procedemos como sigue:
1000 XOR 0010 = 1010
Ahora, cada bit del resultado estará en 0 si el bit correspondiente de los dos operandos son iguales, y en 1 si son diferentes. El bit más significativo del resultado está en 1 indicando que son diferentes, pero tenemos que aislarlo de los demás con un AND para poder usarlo o tomar una decisión:
1010 (resultado anterior) AND 1000 (máscara para aislar el bit más significativo) = 1000
Ahora lo tenemos aislado en el resultado final, que es diferente de cero indicando que los bits más significativo de los operandos son diferentes.
Asignar cero a un registro
Los programadores avanzados de lenguaje ensamblador usan XOR como una manera eficiente y rápida de asignar cero a un registro. Realizar XOR de un valor contra sí mismo siempre resulta en cero (A XOR A siempre es cero), y en muchas arquitecturas esta operación requiere menos ciclos de reloj y/o memoria que cargar un valor cero a un registro (A = 0).
En resumen
Las operaciones bit a bit, o bitwise, pueden encender, apagar, dejar pasar, eliminar, o invertir, bits individualmente o en conjunto, usando la máscara adecuada con un OR, AND, o XOR:
0011 1011 10101 10101 1010 OR 1000 (máscara) AND 1110 (máscara) AND 00111 (máscara) AND 11000 (máscara) XOR 1001 (máscara) = 1011 = 1010 = 00101 = 10000 = 0011 Enciende el Apaga el Deja pasar los 3 Elimina los 3 Invierte los bits bit superior bit inferior bits inferiores bits inferiores inferior y superior
NOT invierte los bits y XOR junto con AND permiten determinar si dos operandos tienen los bits de una determinada posición iguales o diferentes:
NOT 1011 11010 = 0100 XOR 10100 invierte todos = 01110 (0 = bit iguales, 1 = bits diferentes) los bits AND 00010 (se filtra el segundo bits, que es el que interesa) = 00010 Determina si los bits de la segunda posición de los dos operandos son iguales o diferentes 0 = iguales 1 = diferentes
Operaciones de desplazamiento y rotación
Las operaciones de desplazamiento y rotación son:
- Desplazamiento lógico
- Desplazamiento aritmético
- Rotación
- Rotación a través del bit de acarreo
Desplazamientos de bits
Los desplazamientos de bit (bit shifts) son a veces considerados operaciones bit a bit, porque operan en la representación binaria de un número entero en vez de sobre su valor numérico; sin embargo, los desplazamientos de bits no operan en pares de bits correspondientes, y por lo tanto no pueden ser llamados propiamente como "bit a bit" (bit-wise). En estas operaciones los dígitos (bits) son movidos, o desplazados, hacia la izquierda o hacia la derecha. Los registros en un procesador de computador tienen un ancho fijo, así que algunos bits “serán desplazados hacia fuera” ("shifted out"), es decir, "salen" del registro por un extremo, mientras que el mismo número de bits son “desplazados hacia adentro” ("shifted in"), es decir, "entran" por el otro extremo; las diferencias entre los operadores de desplazamiento de bits están en cómo éstos determinan los valores de los bits que entran al registro (desplazamiento hacia adentro) (shifted-in).
Desplazamiento lógico
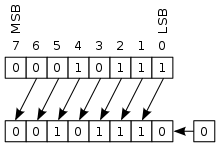

Hay dos desplazamientos lógicos (logical shifts). El desplazamiento lógico hacia la izquierda (left shift) y el desplazamiento lógico hacia la derecha (right shift). En el desplazamiento lógico los bits de un registro son desplazados (movidos) una o más posiciones hacia la derecha o hacia la izquierda. Los bit que salen del registro por un extremo se pierden y en el otro extremo del registro se rellena con un bit cero por cada bit desplazado.
Por ejemplo. Si se tiene en un registro de 8 bits el valor 10110011, y se hace un desplazamiento hacia la izquierda de un bit, todos los bits se mueven una posición hacia la izquierda, el bit de la izquierda se pierde y entra un bit cero de relleno por el lado derecho. En un desplazamiento de un bit hacia la derecha ocurre algo análogo, el bit de la derecha se pierde y el de la izquierda se rellena con un cero:
10110011 10110011 <-- Bits antes del desplazamiento 1 <-- 0110011 <-- 0 0 --> 1011001 --> 1 <-- Desplazamiento 01100110 01011001 <-- Bits después del desplazamiento Desplazamiento Desplazamiento hacia la izquierda hacia la derecha
En determinados procesadores, queda almacenado el último bit que salió con el desplazamiento del registro. En la serie de los procesadores x86 dicho bit queda almacenado en el flag del acarreo.
Moviendo bits
El desplazamiento lógico se usa para mover bits hacia la izquierda o hacia la derecha para colocarlos en la posición adecuada.
Por ejemplo, supongamos que tenemos, en dos registros del tamaño de un byte, a dos dígitos hexadecimales (en representación binaria de 4 bits cada uno), y se quiere empaquetarlos en un solo byte, donde los 4 bits superiores es el hexadecimal más significativo y los 4 bits inferiores es el hexadecimal menos significativo:
0000 1001 <-- Dígito hexadecimal más significativo (hexadecimal 9) 0000 1010 <-- Dígito hexadecimal menos significativo (hexadecimal A)
Para empaquetarlos en un solo byte, primero hay que desplazar el hexadecimal más significativo 4 posiciones hacia la izquierda. (Esto se hace con el desplazamiento lógico hacia la izquierda):
1001 0000 <-- hexadecimal 9, desplazado 4 bits hacia la izquierda para colocarlo en la posición correcta dentro del byte
Luego, se hace un OR de los dos valores que contienen los dígitos hexadecimales para que queden combinados en un solo byte:
0000 1010 <-- Hexadecimal menos significativo A OR 1001 0000 <-- OR con el hexadecimal más significativo 9, el cual ya está en su posición 1001 1010 <-- Byte con los dos hexadecimales empaquetados (hexadecimal 9A)
Ahora tenemos un byte con el valor de 1001 1010, el cual tiene los dos dígitos hexadecimales empaquetados.
Multiplicación y división por 2n, de enteros sin signo
En números enteros sin signo, el desplazamiento lógico hacia la izquierda equivale a una multiplicación por 2 y el desplazamiento lógico hacia la derecha equivale a una división por 2. En la división (desplazamiento hacia la derecha), se pierde el bit menos significativo, dando como resultado un truncamiento del resultado (redondeo hacia abajo, hacia menos infinito). Así, 6 / 2 es igual a 3, pero 7 / 2 es igual a 3,5, pero el 0,5 se pierde quedando el resultado en 3.
Los programadores de lenguaje ensamblador usan esta propiedad para hacer multiplicaciones y divisiones rápidas, de enteros sin signo, por una potencia de 2, en donde n desplazamientos equivalen a multiplicar o dividir por 2n. También, si el procesador no tiene operaciones de multiplicación y división de enteros, o si éstas son muy lentas, se puede multiplicar o dividir usando desplazamientos y sumas para multiplicar y desplazamientos y restas para dividir. Por ejemplo, para multiplicar un entero por 10, se procede como sigue (en el lenguaje ensamblador del x86):
Se quiere multiplicar el contenido del registro EAX por 10:
En las instrucciones de abajo, EAX y EBX son registros del procesador, SHL (shift left), desplaza el registro indicado una posición (un bit) hacia la izquierda (que equivale a multiplicar por 2), MOV copia el registro de la derecha sobre el registro de la izquierda, y ADD suma el registro de la derecha al registro de la izquierda.
SHL EAX, 1 ; EAX = EAX * 2 EAX = 2n ; desplaza a la izquierda el contenido del registro EAX una posición,
; (multiplica EAX por 2)
MOV EBX, EAX ; EBX = EAX EBX = 2n ; copia el registro EAX en EBX, ahora los dos registros tienen 2n
SHL EBX, 1 ; EBX = EBX * 2 EBX = 4n ; multiplica EBX por 2, obteniendo 4n
SHL EBX, 1 ; EBX = EBX * 2 EBX = 8n ; vuelve a multiplicar EBX por 2, obteniendo 8n
ADD EAX, EBX ; EAX = EAX + EBX EAX = 2n + 8n = 10n ; suma EBX (8n) a EAX (2n),
; (ahora EAX tiene el valor original multiplicado por 10)
Desplazamiento aritmético


Los desplazamientos aritméticos son similares a los desplazamientos lógicos, solo que los aritméticos están pensados para trabajar sobre números enteros con signo en representación de complemento a dos en lugar de enteros sin signo. Los desplazamientos aritméticos permiten la multiplicación y la división por dos, de números enteros con signo, por una potencia de dos. Desplazar n bits hacia la izquierda o a la derecha equivale a multiplicar o dividir por 2n, (asumiendo que el valor no hace desbordamiento (overflow o underflow)).
El desplazamiento aritmético hacia la izquierda es exactamente igual al desplazamiento lógico hacia la izquierda. De hecho son dos nombres diferentes para exactamente la misma operación. Al desplazar los bits una posición hacia la izquierda es equivalente a una multiplicación por 2 independientemente de si es un número entero con signo o sin signo. En los procesadores x86, el ensamblador tiene dos pnemónicos para el desplazamiento lógico y el aritmético hacia la izquierda, pero cuando el programa es ensamblado, solo hay un opcode para ambos en la instrucción en lenguaje de máquina.
El desplazamiento aritmético hacia la derecha es diferente al desplazamiento lógico hacia la derecha. En los enteros sin signo, para dividir por 2, se debe usar el desplazamiento lógico, el cual siempre agrega un 0 en el extremo izquierdo por cada desplazamiento de un bit hacia la derecha. En cambio, en los enteros con signo, se debe usar el desplazamiento aritmético hacia la derecha, el cual copia el bit del signo (el bit más significativo (MSB)) en el espacio vacío que queda en el extremo izquierdo cada vez que se hace un desplazamiento de un bit hacia la derecha. De esta manera, se divide efectivamente por 2 al entero con signo.
Si el entero con signo es positivo, (con el bit del signo igual a 0), se insertará el bit 0 del signo en el extremo izquierdo al desplazar un bit hacia la derecha (igual que el desplazamiento lógico hacia la derecha), pero si es un entero negativo, (con el bit del signo igual a 1), se insertará el bit 1 del bit del signo en el extremo izquierdo. De esta manera, el signo del número se preserva con la división por 2 y el número resultante tiene sentido. Si se insertara un 0 a la izquierda a un número negativo (como lo haría el desplazamiento lógico hacia la derecha), en primer lugar, este número negativo cambiaría de signo a positivo, y en segundo lugar, la interpretación de los bits restantes no tendrían sentido.
Estos ejemplos utilizan un registro de 8 bits:
00010111 (Decimal 23) (Desplazamiento aritmético hacia la izquierda de un número positivo) = 00101110 (Decimal 46) (El bit de la izquierda se pierde y un bit 0 se añade a la derecha) 11010111 (Decimal -41) (Desplazamiento aritmético hacia la izquierda de un número negativo) = 10101110 (Decimal -82) (El bit de la izquierda se pierde y un bit 0 se añade a la derecha) 00010111 (Decimal 23) (Desplazamiento aritmético hacia la derecha de un número positivo) = 00001011 (Decimal 11) (El bit de la derecha se pierde y el bit del signo anterior se conserva en el resultado) 11010111 (Decimal -41) (Desplazamiento aritmético hacia la derecha de un número negativo) = 11101011 (Decimal -21) (El bit de la derecha se pierde y el bit del signo anterior se conserva en el resultado)
Si el número binario es tratado como complemento a 1, entonces la misma operación de desplazamiento hacia la derecha resulta en una división por 2n redondeando hacia el cero.
Rotación de bits
Rotación
 |
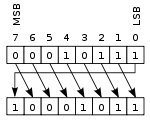 |
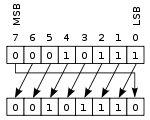
Otra forma de desplazamiento es el desplazamiento circular o rotación de bits. En esta operación, los bits de un registro son “rotados” de una manera circular como si los extremos izquierdo y derecho del registro estuvieran conectados. En la rotación hacia la izquierda, el bit que sale por el extremo izquierdo entrará por el extremo derecho, y viceversa con la rotación hacia la derecha. Esta operación es útil si es necesario conservar todos los bits existentes, y es frecuentemente usada en criptografía digital.
Rotación a través del bit del acarreo
 |
 |
Rotar a través del bit del acarreo es similar a la operación de rotar anterior (rotación sin acarreo). La diferencia está en que los dos extremos del registro están unidos entre sí a través del flag del acarreo, el cual queda en medio de ellos. El bit que sale por un extremo va al flag del acarreo, y el bit original que estaba en el flag del acarreo entra al registro por el extremo opuesto.
Si se fija el flag del acarreo de antemano, una rotación simple a través del acarreo puede simular un desplazamiento lógico o aritmético de una posición. Por ejemplo, si el flag del acarreo contiene 0, después de una rotación hacia la derecha a través del flag del acarreo, equivale a un desplazamiento lógico hacia la derecha, y si el flag del acarreo contiene una copia del bit del signo, equivale a un desplazamiento aritmético hacia la derecha. Por esta razón, algunos microcontroladores tales como los PIC solo tienen las funciones de rotar y rotar a través del acarreo, y no se preocupan de tener instrucciones de desplazamiento aritmético o lógico.
Rotar a través del acarreo es especialmente útil cuando se hacen desplazamientos en números más grandes que el tamaño nativo de la palabra del procesador, porque si, por ejemplo, un número grande es almacenado en dos registros y se quiere desplazar hacia la derecha un bit, el bit que sale del extremo derecho del registro de la izquierda debe entrar por el extremo izquierdo del registro de la derecha. Con rotación a través del acarreo, ese bit es “almacenado” en el flag del acarreo durante el primer desplazamiento hacia la derecha sobre el registro de la izquierda, listo para ser desplazado al registro de la derecha usando una simple rotación con acarreo hacia la derecha y sin usar ninguna preparación extra.
Véase también
- Negación lógica
- Conjunción lógica
- Disyunción lógica
- Disyunción exclusiva
- Lógica binaria
- Álgebra de Boole
- Algoritmo de intercambio usando XOR
- Lista encadenada de XOR
