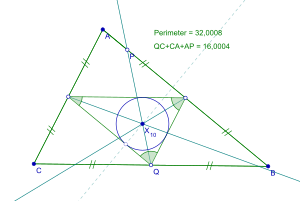
En geometría, el incírculo del triángulo medial de un triángulo es la circunferencia de Spieker, nombrada así por el geómetra alemán Theodor Spieker. Su centro, el punto de Spieker, es el incentro del triángulo medial. El centro de Spieker es también el punto donde los bisectores del perímetro del triángulo que terminan el punto medio de cada lado se intersecan.
El punto de Nagel y el punto mediano de un triángulo son los centros homotéticos de la Circunferencia de Spieker y de la circunferencia inscrita en el triángulo.
Construcción
Para encontrar la circunferencia de Spieker de un triángulo, primero se debe construir el triángulo medial a partir de los puntos medios de cada lado del triángulo original.[1] Luego, la circunferencia se construye de tal manera que cada lado del triángulo medial sea tangente a la circunferencia dentro del triángulo medial, creando la circunferencia.[1] Este centro circular se llama punto de Spieker.
Referencias
Bibliografía
- Johnson, Roger A. (1929). Modern Geometry. Boston: Houghton Mifflin. Dover reprint, 1960.
- Kimberling, Clark (1998). «Triangle centers and central triangles». Congressus Numerantium 129: i-xxv, 1-295.
| Control de autoridades |
|
|---|
Datos: Q451581
Esta página se editó por última vez el 28 nov 2020 a las 11:29.