
A tree structure, tree diagram, or tree model is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, although the chart is generally upside down compared to a biological tree, with the "stem" at the top and the "leaves" at the bottom.
A tree structure is conceptual, and appears in several forms. For a discussion of tree structures in specific fields, see Tree (data structure) for computer science; insofar as it relates to graph theory, see tree (graph theory) or tree (set theory). Other related articles are listed below.
YouTube Encyclopedic
-
1/3Views:1 369 463446 780221 540
-
Data structures: Introduction to Trees
-
Binary Tree Algorithms for Technical Interviews - Full Course
-
Introduction to Trees (Data Structures & Algorithms #9)
Transcription
Hello everyone ! In this lesson, we will introduce you to an interesting data structure that has got its application in a wide number of scenarios in computer science and this data structure is tree. So, far in this series, we have talked about what we can call linear data structures. Array, Linked List, stack and queue, all of these are linear data structures. All of these are basically collections of different kinds in which data is arranged in a sequential manner. In all these structures that I am showing here, we have a logical start and a logical end and then an element in any of these collections can have a next element and e previous element. So, all in all we have linear or sequential arrangement. Now, as we understand, these data structures are ways to store and organize data in computers. For different kinds of data, we use different kinds of data structure. Our choice of data structure depends upon a number of factors. First of all, its about what needs to be stored. A certain data structure can be best fit for a particular kind of data. Then, we may care for the cost of operations. Quite often, we want to minimize the cost of most frequently performed operations. For example, lets say we have a simple list and we are searching for an element in the list most of the time. Then, we may want to store the list or collection as an array in sorted order, so we can perform something like binary search really fast. Another factor can be memory consumption. Sometimes, we may want to minimize the memory usage and finally we may also choose a data structure for ease of implementation, although this may not be the best strategy. Tree is one data structure that's quite often used to represent hierarchical data. For example, lets say we want to show employees in an organization and their positions in organizational hierarchy, then we can show it something like this. Lets say this is organization hierarchy of some company. In this company, John is CEO and john has two direct reports - Steve and Rama. Then Steve has 3 direct reports. Steve is manager of Lee, Bob and Ella. They may be having some designation. Rama also has two direct reports. Then Bob has two direct reports and then Tom has 1 direct report. This particular logical structure that I have drawn here is a Tree. Well, you have to look at this structure upside down and then it will resemble a real tree. The root here is at top and we are branching out in downward direction. Logical representation of tree data structure is always like this. Root at top and branching out in downward direction. Ok, so tree is an efficient way of storing and organizing data that is naturally hierarchical, but this is not the only application of tree in computer science. We will talk about other applications and some of the implementation details like how we can create such a logical structure in computer's memory later. First I want to define tree as a logical model. Tree data structure can be defined as a collection of entities called nodes linked together to simulate hierarchy. Tree is a non-linear data structure. Its a hierarchical structure. The topmost node in the tree is called root of the tree. Each node will contain some data and this can be data of any type. In the tree that I am showing in right here data is name of employee and designation. So, we can have an object with two string fields one to store name and another to store designation. Okay, so each node will contain some data and may contain link or reference to some other nodes that can be called its children. Now I am introducing you to some vocabulary that we use for tree data structure. What I am going to do here is , I am going to number these Nodes in the left tree. So, I can refer to these Nodes using these numbers. I am numbering these nodes only for my convenience. its not to show any order. Ok, coming back, as i had said each node will have some data. We call fill in some data in these circles. It can be data of any type. it can be an integer or a character or a string or we can simple assume that there is some data filled inside these nodes and we are not showing it. Ok, as we were discussing, a node may have link or reference to some other nodes that will be called its children. Each arrow in this structure here is a link. Ok, now as you can see, the root node which is numbered 1 by me and once again this number is not indicative of any order. I could have called the root node number 10 also. So, root node has link to these two nodes numbered 2 and 3. So, 2 and 3 will be called children of 1 and node 1 will be called parent of nodes 2 and 3. I'll write down all these terms that I am talking about. We mentioned root, children and parent. In this tree, one is a parent of , 1 is parent of 2 and 3. 2 is child of 1. And now, 4 , 5 and 6 are children of 2. So, node 2 is child of node 1, but parent of nodes 4, 5 and 6. Children of same parent are called sibling. I am showing siblings in same color here. 2 and 3 are sibling. Then, 4, 5 and 6 are sibling, then 7,8 are sibling and finally 9 and 10 are sibling. I hope you are clear with these terms now. The topmost node in the tree is called root. Root would be the only node without a parent. And then, if a node has a direct link to some other node, then we have a parent child relationship between the nodes. Any node in the tree that does not have a child is called leaf node. All these nodes marked in black here are leaves. So, leaf is one more term. All other nodes with at least one child can be called internal nodes. And we can have some more relationships like parent of parent can be called grand-parent. So, 1 is grand-parent of 4 and 4 is grand-child of 1. In general, if we can go from node A to B walking through the links and remember these links are not bidirectional. We have a link from 1 to 2, so we can go from 1 to 2, but we cannot go from 2 to 1. When we are walking the tree, we can walk in only one direction. OK, so if we can go from node A to node B, then A can be called ancestor of B and B can be called descendant of A. Lets pick up this node numbered 10. 1, 2 and 5 are all ancestors of 10 and 10 is a descendant of all of these nodes. We can walk from any of these nodes to 10. Ok, let me now ask you some questions to make sure you understand things. What are the common ancestors of 4 and 9? Ancestors of 4 are 1 and 2 and ancestors of 9 are 1,2 and 5. So, common ancestors will be 1 and 2. Ok, next question. Are 6 and 7 sibling? Sibling must have same parent. 6 and 7 do not have same parent. They have same grand-parent. one is grandparent of both. Nodes not having same parent but having same grandparent can be called cousins. So, 6 and 7 are cousins. These relationships are really interesting. We can also say that node number 3 is uncle of node number 6 because its sibling of 2 which is father of 6 or i should say parent of 6. So, we have quite some terms in vocabulary of tree. Ok, now I will talk about some properties of tree. Tree can be called a recursive data structure. We can define tree recursively as a structure that consists of a distinguished node called root and some sub-trees and the arrangement is such that root of the tree contains link to roots of all the sub-trees. T1, T2 and T3 in this figure are sub-trees. In the tree that I have drawn in left here, we have 2 sub-trees for root node. I am showing the root node in red, the left sub-tree in brown and right sub-tree in yellow. We can further split the left sub-tree and look at it like node number 2 is root of this sub-tree and this particular tree with node number 2 as root has 3 sub-trees. i am showing the three sub-trees in 3 different colors. Recursion basically is reducing something in a self similar manner. This recursive property of tree will be used everywhere in all implementation and usage of tree. The next property that I want to talk about is - in a tree with n nodes, there will be exactly n-1 links or edges. Each arrow in this figure can be called a link or an edge. All nodes except the root node will have exactly 1 incoming edge. If you can see, I'll pick this node numbered 2. There is only one incoming link. This is incoming link and these three are outgoing links. There will be one link for each parent-child relationship. So, in a valid tree if there are n nodes, there will be exactly n-1 edges. One incoming edge for each node except the root. Ok, now i want to talk about these two properties called depth and height. Depth of some node X in a tree can be defined as length of the path from root to Node X. Each edge in the path will contribute one unit to the length. So, we can also say number of edges in path from root to X. The depth of root node will be zero. Lets pick some other node. For this node, numbered 5, we have 2 edges in the path from root. So, the depth of this node is 2. In this tree here, depth of nodes 2 and 3 is 1. Depth of nodes 4,5,6,7 and 8 is 2 and the depth of nodes 9, 10 and 11 is 3. Ok, now height of a node in tree can be defined as number of edges in longest path from that node to a leaf node. So, height of some node X will be equal to number of edges in longest path from X to a leaf. In this figure, for node 3, the longest path from this node to any leaf is 2. So, height of node 3 is 2. Node 8 is also a leaf node. I'll mark all the leaf nodes here. A leaf node is a node with zero child. The longest path from node 3 to any of the leaf nodes is 2. So, the height of Node 3 is 2. Height of leaf nodes will be 0. So, what will be the height of root node in this tree. We can reach all the leaves from root node. number of edges in longest path is 3. So, height of the root node here is 3. We also define height of a tree. Height of tree is defined as height of root node. Height of this tree that I am showing here is 3. Height and depth are different properties and height and depth of a node may or may not be same. We often confuse between the two. Based on properties, trees are classified into various categories. There are different kinds of trees that are used in different scenarios. Simplest and most common kind of tree is a tree with this property that any node can have at most 2 children. In this figure, node 2 has 3 children. I am getting rid of some nodes and now this is a binary tree. Binary tree is most famous and throughout this series, we will mostly be talking about binary trees. The most common way of implementing tree is dynamically created nodes linked using pointers or references, just the way we do for linked list. We can look at the tree like this. in this structure that I have drawn in right here, node has 3 fields. one of the fields is to store data. Lets say middle cell is to store data. The left cell is to store the address of the left child. And the right cell is to store address of right child. Because this is a binary tree, we cannot have more than two children. We can all one of the children left child and another right child. Programmatically, in C or C++, we can define a node as a structure like this. We have three fields here - one to store data, lets say data type is integer. I have filled in some data in these nodes. So, in each node, we have 3 fields. We have an integer variable to store the data and then we have 2 pointers to Node, one to store the address of the left child that will be the root of the left sub-tree and another to store the address of the right child. We have kept only 2 pointers because we can have at most 2 children in binary tree. This particular definition of Node can be used only for a binary tree. For generic trees that can have any number of children, we use some other structure and I'll talk about it in later lessons. In fact, we will discuss implementation in detail in later lessons. This is just to give you a brief idea of how things will be like in implementation. Ok, so this is cool. We understand what a tree data structure is, but in the beginning we had said that storing naturally hierarchical data is not the only application of tree. So, lets quickly have a look at some of the applications of tree in computer science. First application of course is storing naturally hierarchical data. For example, the file system on your disc drive, the file and folder hierarchy is naturally hierarchical data. its stored in the form of tree. Next application is organizing data, organizing collections for quick search, insertion and deletion. For example, binary search tree that we'll be discussing a lot in next couple of lessons can give us order of log N time for searching an element in it. A special kind of tree called Trie is used , is use to store dictionary. Its really fast and efficient and is used for dynamic spell checking. Tree data structure is also used in network routing algorithms and this list goes on. We'll talk about different kinds of trees and their applications in later lessons. I'll stop here now. This is good for an introduction. In next couple of lessons, we will talk about binary search trees and its implementation. This is it for this lesson. Thanks for watching !
Terminology and properties
The tree elements are called "nodes". The lines connecting elements are called "branches". Nodes without children are called leaf nodes, "end-nodes", or "leaves".
Every finite tree structure has a member that has no superior. This member is called the "root" or root node. The root is the starting node. But the converse is not true: infinite tree structures may or may not have a root node.
The names of relationships between nodes model the kinship terminology of family relations. The gender-neutral names "parent" and "child" have largely displaced the older "father" and "son" terminology. The term "uncle" is still widely used for other nodes at the same level as the parent, although it is sometimes replaced with gender-neutral terms like "ommer".[1]
- A node's "parent" is a node one step higher in the hierarchy (i.e. closer to the root node) and lying on the same branch.
- "Sibling" ("brother" or "sister") nodes share the same parent node.
- A node's "uncles" (sometimes "ommers") are siblings of that node's parent.
- A node that is connected to all lower-level nodes is called an "ancestor". The connected lower-level nodes are "descendants" of the ancestor node.
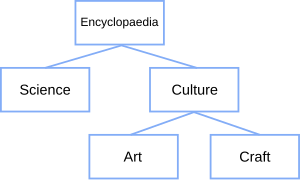
In the example, "encyclopedia" is the parent of "science" and "culture", its children. "Art" and "craft" are siblings, and children of "culture", which is their parent and thus one of their ancestors. Also, "encyclopedia", as the root of the tree, is the ancestor of "science", "culture", "art" and "craft". Finally, "science", "art" and "craft", as leaves, are ancestors of no other node.
Tree structures can depict all kinds of taxonomic knowledge, such as family trees, the biological evolutionary tree, the evolutionary tree of a language family, the grammatical structure of a language (a key example being S → NP VP, meaning a sentence is a noun phrase and a verb phrase, with each in turn having other components which have other components), the way web pages are logically ordered in a web site, mathematical trees of integer sets, et cetera.
The Oxford English Dictionary records use of both the terms "tree structure" and "tree-diagram" from 1965 in Noam Chomsky's Aspects of the Theory of Syntax.[2]
In a tree structure there is one and only one path from any point to any other point.
Computer science uses tree structures extensively (see Tree (data structure) and telecommunications.)
For a formal definition see set theory, and for a generalization in which children are not necessarily successors, see prefix order.
Examples of tree structures


- Internet:
- Vacuum tubes
- Document Object Model's logical structure,[3] Yahoo! subject index, Curlie
- Operating system: directory structure
- Information management: Dewey Decimal System, PSH, this hierarchical bulleted list
- Management: hierarchical organizational structures
- Computer science:
- Biology: evolutionary tree
- Business: pyramid selling scheme
- Project management: work breakdown structure
- Linguistics:
- (Syntax) Phrase structure trees
- (Historical Linguistics) Tree model of language change
- Sports: business chess, playoffs brackets
- Mathematics: Von Neumann universe
- Group theory: descendant trees
Representing trees
There are many ways of visually representing tree structures. Almost always, these boil down to variations, or combinations, of a few basic styles:
Classical node-link diagrams
Classical node-link diagrams, that connect nodes together with line segments:
| encyclopedia | ||
|---|---|---|
| / culture |
\ science | |
| / art |
\ craft | |
Nested sets
Nested sets that use enclosure or containment to show parenthood; examples include TreeMaps, fractal maps, and Euler diagrams:
Layered "icicle" diagrams
Layered "icicle" diagrams that use alignment/adjacency.
| encyclopedia | ||
|---|---|---|
| culture | science | |
| art | craft | |
Outlines and tree views
Lists or diagrams that use indentation, sometimes called "outlines" or "tree views".
An outline:
- encyclopedia
- culture
- art
- craft
- science
- culture
A tree view:
- encyclopedia
- culture
- art
- craft
- science
- culture
Nested parentheses
A correspondence to nested parentheses was first noticed by Sir Arthur Cayley:
((art,craft)culture,science)encyclopedia
or
encyclopedia(culture(art,craft),science)
Radial trees
Trees can also be represented radially:
| art \ |
craft / |
|---|---|
| culture | | |
| encyclopedia | |
| | science | |
See also
- Kinds of trees
- B-tree
- Dancing tree
- Decision tree
- Left-child right-sibling binary tree
- Porphyrian tree
- Tree (data structure)
- Tree (graph theory)
- Tree (set theory)
- Related articles
References
- ^ "Ethereum Glossary". GitHub. Archived from the original on 25 April 2019. Retrieved 17 April 2019.
- ^ "tree". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
- ^ "What is the Document Object Model?". W3C Architecture domain. Archived from the original on 2012-02-12. Retrieved 2006-12-05.
Further reading
Identification of some of the basic styles of tree structures can be found in:
- Jacques Bertin, Semiology of Graphics, 1983, University of Wisconsin Press (2nd edition 1973, ISBN 978-0299090609;
- Donald E. Knuth (1968). The Art of Computer Programming. Volume 1: Fundamental Algorithms. Addison-Wesley. pp. 309–310.
- Brian Johnson and Ben Shneiderman, "Tree-maps: A space-filling approach to the visualization of hierarchical information structures", in Proceedings of IEEE Visualization (VIS), 1991, pp. 284–291, ISBN 0-8186-2245-8;
- Peter Eades, Tao Lin, and Xuemin Lin, "Two Tree Drawing Conventions", International Journal of Computational Geometry and Applications, 1993, volume 3, number 2, pp. 133–153.
- Manuel Lima (2014). The Book of Trees: Visualizing Branches of Knowledge (1st ed.). New York: Princeton Architectural Press. ISBN 978-1-616-89218-0.
External links
- Visualization of phylogenetic trees on the T-REX server
- Using a tree structure to design a business process – from the Society for Technical Communication
