Trapezoidal rule (differential equations)

In numerical analysis and scientific computing, the trapezoidal rule is a numerical method to solve ordinary differential equations derived from the trapezoidal rule for computing integrals. The trapezoidal rule is an implicit second-order method, which can be considered as both a Runge–Kutta method and a linear multistep method.

YouTube Encyclopedic

1/3
Views:
406
39 125
417 889

Transcription

Method

Suppose that we want to solve the differential equation

y'=f(t,y).

The trapezoidal rule is given by the formula

y_{n+1}=y_{n}+{\tfrac {1}{2}}h{\Big (}f(t_{n},y_{n})+f(t_{n+1},y_{n+1}){\Big )},

where

h=t_{n+1}-t_{n}

is the step size.^[1]

This is an implicit method: the value $y_{n+1}$ appears on both sides of the equation, and to actually calculate it, we have to solve an equation which will usually be nonlinear. One possible method for solving this equation is Newton's method. We can use the Euler method to get a fairly good estimate for the solution, which can be used as the initial guess of Newton's method.^[2] Cutting short, using only the guess from Eulers method is equivalent to performing Heun's method.

Motivation

Integrating the differential equation from $t_{n}$ to $t_{n+1}$ , we find that

y(t_{n+1})-y(t_{n})=\int _{t_{n}}^{t_{n+1}}f(t,y(t))\,\mathrm {d} t.

The trapezoidal rule states that the integral on the right-hand side can be approximated as

\int _{t_{n}}^{t_{n+1}}f(t,y(t))\,\mathrm {d} t\approx {\tfrac {1}{2}}h{\Big (}f(t_{n},y(t_{n}))+f(t_{n+1},y(t_{n+1})){\Big )}.

Now combine both formulas and use that

y_{n}\approx y(t_{n})

and

y_{n+1}\approx y(t_{n+1})

to get the trapezoidal rule for solving ordinary differential equations.^[3]

Error analysis

It follows from the error analysis of the trapezoidal rule for quadrature that the local truncation error $\tau _{n}$ of the trapezoidal rule for solving differential equations can be bounded as:

|\tau _{n}|\leq {\tfrac {1}{12}}h^{3}\max _{t}|y'''(t)|.

Thus, the trapezoidal rule is a second-order method.^{[citation needed]} This result can be used to show that the global error is

O(h^{2})

as the step size

h

tends to zero (see big O notation for the meaning of this).^[4]

Stability

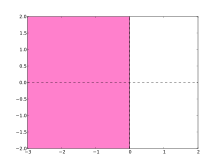
The region of absolute stability for the trapezoidal rule is

\{z\in \mathbb {C} \mid \operatorname {Re} (z)<0\}.

This includes the left-half plane, so the trapezoidal rule is A-stable. The second Dahlquist barrier states that the trapezoidal rule is the most accurate amongst the A-stable linear multistep methods. More precisely, a linear multistep method that is A-stable has at most order two, and the error constant of a second-order A-stable linear multistep method cannot be better than the error constant of the trapezoidal rule.^[5]

In fact, the region of absolute stability for the trapezoidal rule is precisely the left-half plane. This means that if the trapezoidal rule is applied to the linear test equation y' = λy, the numerical solution decays to zero if and only if the exact solution does.

Notes

^ Iserles 1996, p. 8; Süli & Mayers 2003, p. 324
^ Süli & Mayers 2003, p. 324
^ Iserles 1996, p. 8; Süli & Mayers 2003, p. 324
^ Iserles 1996, p. 9; Süli & Mayers 2003, p. 325
^ Süli & Mayers 2003, p. 324

References

Iserles, Arieh (1996), A First Course in the Numerical Analysis of Differential Equations, Cambridge University Press, ISBN 978-0-521-55655-2.
Süli, Endre; Mayers, David (2003), An Introduction to Numerical Analysis, Cambridge University Press, ISBN 0521007941.

v t e Numerical methods for integration
First-order methods	Euler method Backward Euler Semi-implicit Euler Exponential Euler
Second-order methods	Verlet integration Velocity Verlet Trapezoidal rule Beeman's algorithm Midpoint method Heun's method Newmark-beta method Leapfrog integration
Higher-order methods	Exponential integrator Runge–Kutta methods List of Runge–Kutta methods Linear multistep method General linear methods Backward differentiation formula Yoshida Gauss–Legendre method
Theory	Symplectic integrator

From Wikipedia, the free encyclopedia