| Transitive binary relations | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
All definitions tacitly require the homogeneous relation be transitive: for all if and then |
In mathematics, a binary relation on a set is reflexive if it relates every element of to itself.[1][2]
An example of a reflexive relation is the relation "is equal to" on the set of real numbers, since every real number is equal to itself. A reflexive relation is said to have the reflexive property or is said to possess reflexivity. Along with symmetry and transitivity, reflexivity is one of three properties defining equivalence relations.
YouTube Encyclopedic
-
1/5Views:308 868345 48325 205165 9322 080
-
Reflexive, Symmetric, and Transitive Relations on a Set
-
Types of Relations (Part 1)
-
Reflexive Relation - Explained with Examples
-
Reflexive, Symmetric, Transitive Tutorial
-
Reflexive Relations and Examples
Transcription
Definitions
Let be a binary relation on a set which by definition is just a subset of For any the notation means that while "not " means that
The relation is called reflexive if for every or equivalently, if where denotes the identity relation on The reflexive closure of is the union which can equivalently be defined as the smallest (with respect to ) reflexive relation on that is a superset of A relation is reflexive if and only if it is equal to its reflexive closure.
The reflexive reduction or irreflexive kernel of is the smallest (with respect to ) relation on that has the same reflexive closure as It is equal to The reflexive reduction of can, in a sense, be seen as a construction that is the "opposite" of the reflexive closure of For example, the reflexive closure of the canonical strict inequality on the reals is the usual non-strict inequality whereas the reflexive reduction of is
Related definitions
There are several definitions related to the reflexive property. The relation is called:
- irreflexive, anti-reflexive or aliorelative
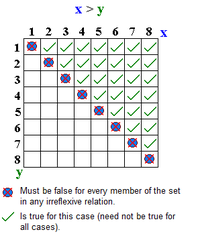
- [3] if it does not relate any element to itself; that is, if holds for no A relation is irreflexive if and only if its complement in is reflexive. An asymmetric relation is necessarily irreflexive. A transitive and irreflexive relation is necessarily asymmetric.
- left quasi-reflexive
- if whenever are such that then necessarily [4]
- right quasi-reflexive
- if whenever are such that then necessarily
- quasi-reflexive
- if every element that is part of some relation is related to itself. Explicitly, this means that whenever are such that then necessarily and Equivalently, a binary relation is quasi-reflexive if and only if it is both left quasi-reflexive and right quasi-reflexive. A relation is quasi-reflexive if and only if its symmetric closure is left (or right) quasi-reflexive.
- antisymmetric
- if whenever are such that then necessarily
- coreflexive
- if whenever are such that then necessarily [5] A relation is coreflexive if and only if its symmetric closure is anti-symmetric.
A reflexive relation on a nonempty set can neither be irreflexive, nor asymmetric ( is called asymmetric if implies not ), nor antitransitive ( is antitransitive if implies not ).
Examples
Examples of reflexive relations include:
- "is equal to" (equality)
- "is a subset of" (set inclusion)
- "divides" (divisibility)
- "is greater than or equal to"
- "is less than or equal to"
Examples of irreflexive relations include:
- "is not equal to"
- "is coprime to" on the integers larger than 1
- "is a proper subset of"
- "is greater than"
- "is less than"
An example of an irreflexive relation, which means that it does not relate any element to itself, is the "greater than" relation () on the real numbers. Not every relation which is not reflexive is irreflexive; it is possible to define relations where some elements are related to themselves but others are not (that is, neither all nor none are). For example, the binary relation "the product of and is even" is reflexive on the set of even numbers, irreflexive on the set of odd numbers, and neither reflexive nor irreflexive on the set of natural numbers.
An example of a quasi-reflexive relation is "has the same limit as" on the set of sequences of real numbers: not every sequence has a limit, and thus the relation is not reflexive, but if a sequence has the same limit as some sequence, then it has the same limit as itself. An example of a left quasi-reflexive relation is a left Euclidean relation, which is always left quasi-reflexive but not necessarily right quasi-reflexive, and thus not necessarily quasi-reflexive.
An example of a coreflexive relation is the relation on integers in which each odd number is related to itself and there are no other relations. The equality relation is the only example of a both reflexive and coreflexive relation, and any coreflexive relation is a subset of the identity relation. The union of a coreflexive relation and a transitive relation on the same set is always transitive.
Number of reflexive relations
The number of reflexive relations on an -element set is [6]
| Elements | Any | Transitive | Reflexive | Symmetric | Preorder | Partial order | Total preorder | Total order | Equivalence relation |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 1 |
| 2 | 16 | 13 | 4 | 8 | 4 | 3 | 3 | 2 | 2 |
| 3 | 512 | 171 | 64 | 64 | 29 | 19 | 13 | 6 | 5 |
| 4 | 65,536 | 3,994 | 4,096 | 1,024 | 355 | 219 | 75 | 24 | 15 |
| n | 2n2 | 2n(n−1) | 2n(n+1)/2 | ∑n k=0 k!S(n, k) |
n! | ∑n k=0 S(n, k) | |||
| OEIS | A002416 | A006905 | A053763 | A006125 | A000798 | A001035 | A000670 | A000142 | A000110 |
Note that S(n, k) refers to Stirling numbers of the second kind.
Philosophical logic
Authors in philosophical logic often use different terminology. Reflexive relations in the mathematical sense are called totally reflexive in philosophical logic, and quasi-reflexive relations are called reflexive.[7][8]
Notes
- ^ Levy 1979, p. 74
- ^ Schmidt 2010
- ^ This term is due to C S Peirce; see Russell 1920, p. 32. Russell also introduces two equivalent terms to be contained in or imply diversity.
- ^ The Encyclopedia Britannica calls this property quasi-reflexivity.
- ^ Fonseca de Oliveira & Pereira Cunha Rodrigues 2004, p. 337
- ^ On-Line Encyclopedia of Integer Sequences A053763
- ^ Hausman, Kahane & Tidman 2013, pp. 327–328
- ^ Clarke & Behling 1998, p. 187
References
- Clarke, D.S.; Behling, Richard (1998). Deductive Logic – An Introduction to Evaluation Techniques and Logical Theory. University Press of America. ISBN 0-7618-0922-8.
- Fonseca de Oliveira, José Nuno; Pereira Cunha Rodrigues, César de Jesus (2004), "Transposing relations: from Maybe functions to hash tables", Mathematics of Program Construction, Springer: 334–356
- Hausman, Alan; Kahane, Howard; Tidman, Paul (2013). Logic and Philosophy – A Modern Introduction. Wadsworth. ISBN 1-133-05000-X.
- Levy, A. (1979), Basic Set Theory, Perspectives in Mathematical Logic, Dover, ISBN 0-486-42079-5
- Lidl, R.; Pilz, G. (1998), Applied abstract algebra, Undergraduate Texts in Mathematics, Springer-Verlag, ISBN 0-387-98290-6
- Quine, W. V. (1951), Mathematical Logic, Revised Edition, Reprinted 2003, Harvard University Press, ISBN 0-674-55451-5
- Russell, Bertrand (1920). Introduction to Mathematical Philosophy (PDF) (2nd ed.). London: George Allen & Unwin, Ltd. (Online corrected edition, Feb 2010)
- Schmidt, Gunther (2010), Relational Mathematics, Cambridge University Press, ISBN 978-0-521-76268-7
External links
- "Reflexivity", Encyclopedia of Mathematics, EMS Press, 2001 [1994]