| Part of the Politics series |
| Electoral systems |
|---|
 |
|
|
The term ranked voting, also known as preferential voting or ranked-choice voting, pertains to any voting system where voters indicate a rank to order candidates or options—in a sequence from first, second, third, and onwards—on their ballots. Ranked voting systems vary based on the ballot marking process, how preferences are tabulated and counted, the number of seats available for election, and whether voters are allowed to rank candidates equally.
Ranked voting systems are opposed to cardinal voting methods, which allow voters to indicate how strongly they support different candidates (e.g. on a scale from 0-10). Cardinal ballots provide more information than ordinal ballots and as a result, they are not subject to many of the problems in ranked-choice voting (such as Arrow's impossibility theorem).
The most commonly-used example of a ranked-choice system is the familiar plurality voting rule, which gives one "point" (vote) to the candidate ranked first, and zero points to all others (making additional marks unnecessary). This is an example of a positional system, a system that assigns points to candidates based on their ranking in the ordering. Another example (Dowdall's method) assigns 1, 1⁄2, 1⁄3... points to the 1st, 2nd, 3rd... candidates on each ballot. In addition, some countries elect policymakers by instant-runoff voting, a staged variant of the plurality system.
In the US, the term ranked-choice voting is most commonly used by organizations like FairVote and RepresentUs to refer to instant-runoff voting or single transferable vote. However, it has also been used for other ranked voting systems.[1]
YouTube Encyclopedic
-
1/5Views:4363 000664902175 992
-
Ranked Voting - The Reallocation Process
-
Ranked Choice Voting
-
Ranked Voting: Marking The Ballot
-
Webinar 2021: The Basics of Ranked Choice Voting Administration
-
What is a ranked ballot?
Transcription
History of ranked voting
The earliest known proposals for a ranked voting system other than plurality can be traced to the works Ramon Llull in the late 13th century, who developed what would later be known as Copeland's method.
The modern analysis of ranked voting began when Jean-Charles de Borda published a paper in 1781, advocating for the Borda count method that now bears his name. This methodology drew criticism from the Marquis de Condorcet, who developed his own methods after arguing Borda's approach did not accurately reflect group preferences.[2]
Interest in ranked voting continued throughout the 19th century. Danish pioneer Carl Andræ formulated the single transferable vote (STV) system, which was adopted by his native Denmark in 1855. Condorcet had previously considered the similar instant-runoff system before rejecting it as paradoxical.[3][4]
Theoretical exploration of electoral processes was initiated by a 1948 paper from Duncan Black,[5] which was soon followed by Kenneth Arrow's research on the consistency of voting criteria. This subject has since continued to receive scholarly interest under social choice theory, a branch of welfare economics.
Adoption
Plurality voting is the most common voting system. It has been in widespread use since the earliest democracies.
The single transferable vote (STV) system was adopted by Denmark in 1855.
Ranked voting first saw governmental use in the 1890s in Tasmania, deploying the STV system. Its broader adoption in Australia began in the 1910s.[6] By the 1920s, ranked voting had expanded globally. It was used in Ireland, South Africa, and approximately 20 cities each in Canada and the U.S. STV was adopted for governmental elections in Ireland, Malta, and Canada (specifically Alberta and Manitoba) beginning in the 1920s.
In more recent years, ranked choice voting has seen greater adoption in the United States. In November 2016, the voters of Maine narrowly passed Question 5, approving instant-runoff voting for all elections. This was first put to use in 2018, marking the inaugural use of a ranked choice voting system in a statewide election in the United States. Later, in November 2020, Alaska voters passed Measure 2, bringing ranked choice voting into effect from 2022.[7][8]
Single-winner ranked voting is used in the election of national-level politicians from the states of Maine[9] and Alaska[10] within the United States. Nauru uses a version of ranked voting called the Dowdall system. For certain local elections in New Zealand, ranked voting is used.[11] Moreover, in the United States, some cities, counties, and federal primaries across 16 states, as well as 5 additional states' overseas voters for federal elections, employ ranked voting.
A form of ranked voting was also used in Slovenia for electing the two minority representatives; it was replaced by the first-past-the-post system in 2021.[12]
Theoretical foundations of ranked voting
Condorcet criterion
Many concepts formulated by the Marquis de Condorcet in the 18th century continue to significantly impact the field. One of these concepts is the Condorcet winner, a candidate preferred over all others by a majority of voters. A voting system that consistently elects this candidate, if one exists, is known as Condorcet consistent or as satisfying the Condorcet criterion. Such systems are referred to as Condorcet methods.
However, in elections where no Condorcet winner exists, a Condorcet cycle is likely to occur, best explained through an example. Suppose an election involves three candidates - A, B, and C, with 30 voters such that ten vote C–B–A, ten vote B–A–C, and ten vote A–C–B. In this case, no Condorcet winner exists. Specifically, A cannot be a Condorcet winner as two-thirds of voters prefer B over A. Similarly, B cannot be the winner as two-thirds prefer C over B, and C cannot win as two-thirds prefer A over C. This forms a cycle where the search for a Condorcet winner fails to find one.
Spatial voting models
| Ballot | Count |
|---|---|
| A–B–C | 36 |
| B–A–C | 15 |
| B–C–A | 15 |
| C–B–A | 34 |
Spatial voting models, initially proposed by Duncan Black and further developed by Anthony Downs, provide a theoretical framework for understanding electoral behavior. In these models, each voter and candidate is positioned within an ideological space that can span multiple dimensions. It is assumed that voters tend to favor candidates who closely align with their ideological position over those more distant. A political spectrum is an example of a one-dimensional spatial model.
The accompanying diagram presents a simple one-dimensional spatial model, illustrating the voting methods discussed in subsequent sections of this article. It is assumed that supporters of candidate A cast their votes in the order of A-B-C, while candidate C's supporters vote in the sequence of C-B-A. Supporters of candidate B are equally divided between listing A or C as their second preference. From the data in the accompanying table, if there are 100 voters, the distribution of ballots will reflect the positioning of voters and candidates along the ideological spectrum.
Spatial models offer significant insights because they provide an intuitive visualization of voter preferences. These models give rise to an influential theorem—the median voter theorem—attributed to Duncan Black. This theorem stipulates that within a broad range of spatial models, including all one-dimensional models and all symmetric models across multiple dimensions, a Condorcet winner is guaranteed to exist. Moreover, this winner is typically the candidate closest to the median of the voter distribution.
Applying these principles to the illustrated diagram reveals a Condorcet winner, candidate B, who is preferred over candidate A by 64% of voters and over candidate C by 66%. Consistent with the median voter theorem, the Condorcet winner aligns closely with the median of the voter distribution.
Other theorems
The implications of Arrow's impossibility theorem cast a shadow on the promise of ranked voting. While the median voter theorem demonstrates the feasibility of creating a voting method that functions flawlessly for a broad spectrum of voter preferences, Arrow's theorem posits the impossibility of devising a system that operates without fail in every conceivable scenario.
The true reflection of electoral behavior—whether it aligns more closely with the optimism posited by Black or the pessimism suggested by Arrow—is a question best answered through empirical investigation. Certain studies, including a notable publication by Tideman and Plassman,[13] propose that simplistic spatial models that adhere to the median voter theorem accurately emulate observed voter behavior. Adding to the discourse of pessimistic views, Gibbard's theorem, put forth by Allan Gibbard, asserts the inevitability of susceptibility to tactical voting in any voting system.
Borda count
| Candidate | Score |
|---|---|
| A | 87 |
| B | 130 |
| C | 83 |
The Borda count is a ranking system that assigns scores to each candidate based on their position in each ballot. If m is the total number of candidates, the candidate ranked first on a ballot receives m - 1 points, the second receives m - 2, and so on, until the last-ranked candidate who receives zero. In the given example, candidate B emerges as the winner with 130 out of a total 300 points.
While Borda count is simple to administer, it does not meet the Condorcet criterion. It has a significant limitation in that its result can be heavily influenced by the entry of candidates who themselves have no real possibility of winning.
Other positional systems
Systems that award points in a similar way but possibly with a different formula are called positional systems. The score vector (m - 1, m - 2,..., 0) is associated with the Borda count, (1, 1/2, 1/3,..., 1/m) defines the Dowdall system and (1, 0,... , 0) equates to first-past-the-post.
Alternative vote (instant-runoff voting)
| Candidate | Count | ||
|---|---|---|---|
| 1st round | 2nd round | 3rd round | |
| A (votes marked A-B) | 36 | 51 | 51 |
| B (15 votes marked B-A; 15 marked B-C) | 30 | 0 | 0 |
| C (votes marked C-B) | 34 | 49 | 49 |
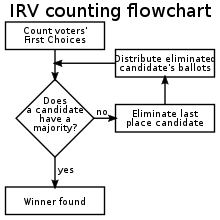
The alternative vote (AV), also known as instant-runoff voting and as ranked-choice voting in the United States, is a voting method that sequentially eliminates candidates in a series of rounds until a winner emerges. In this system, voters rank candidates in order of preference. If a candidate does not receive a majority of first-choice votes, the candidate with the fewest votes is eliminated, and their votes are redistributed according to the voters' next preferences. This process continues until one candidate receives a majority of the remaining votes.
In the given example, Candidate A is declared the winner in the second round, having received a majority of votes through the accumulation of first-choice votes and redistributed votes from Candidate B. This system embodies the voters' preferences between the final candidates, stopping when a candidate garners the preference of a majority of voters.
This method, unlike party-list proportional representation (PR), examines each transferred vote to respect the voter's ranking rather than allocating seats from a derived statistical table. Thus, it ensures a more accurate representation of voters' preferences.
IRV is notable in that it does not fulfill the Condorcet winner criterion, a property held by many other ranked voting systems. Furthermore, unlike its counterparts, IRV generally does not accommodate tied preferences, except occasionally among a voter's least preferred candidates. An adapted version of the single transferable vote (STV) system, intended for party ranking, was proposed for use in German elections in 2013.[14] This proposed system is referred to as the spare vote.[15]
Single transferable vote
An example of an STV election:
There are three positions to be elected, with a total of 100 votes. The quota, determined by the Droop method, is 26 votes.
| Candidate | Count | |||
|---|---|---|---|---|
| 1st round | 2nd round | 3rd round | 4th round | |
| A (votes marked A-B) | 26 (elected) | Elected | ||
| B (votes marked B-E) | 18 | 26 (elected) | Elected | |
| C (votes marked C-D) | 17 | 17 | 17 (elected) | Elected (as last remaining candidate to fill final seat) |
| D (votes marked D-C) | 16 | 16 | 16 | Eliminated |
| E (votes marked E-B) | 15 | 15 | Eliminated | |
| F (votes marked F-B) | 8 | Eliminated | ||
The Single transferable vote (STV) is a multi-winner method and a proportional version of IRV. Like IRV, STV allows for contingent voting based on secondary preferences, which only come into play if the first preference does not lead to an effective result. With STV, voters cast one vote with the possibility to mark back-up preferences. Initially, a voter's ballot is allocated to their most preferred candidate. After a candidate reaches the quota and is elected, surplus votes are transferred from this winner to remaining hopefuls based on the voter's preference order. If there are still vacant seats, the least performing candidates are eliminated, and their votes are transferred to the remaining contenders. Different versions of STV might use varying methodologies for eliminating candidates and transferring votes.
Minimax
| Candidate preference comparison | Second candidate | |||
|---|---|---|---|---|
| A | B | C | ||
| First candidate | A | – | 36:64 | 51:49 |
| B | 64:36 | – | 66:34 | |
| C | 49:51 | 34:66 | – | |
The Minimax voting system determines the winner by constructing a comparison table of candidate preferences, as shown above. This table illustrates the preferences between each pair of distinct candidates (A, B, C). The cell value x:y represents that x voters prefer the first candidate over the second, while y voters have the opposite preference. This data is derived from the ranked votes provided in the Spatial Model section above.
Each row identifies the least satisfactory outcome (i.e., minimal preference) for the first candidate, highlighted in bold. The winning candidate is the one whose least satisfactory outcome is most favorable.
In this specific example, candidate B is the winner. Despite B's worst performance being a 64:36 victory margin over candidate A, this is the most favorable least satisfactory result when compared to those of the other candidates.
The Minimax method, which is straightforward in determining the winner from a set of ballots, satisfies the Condorcet criterion. It elects the Condorcet winner, if one exists. Otherwise, it selects the candidate who comes closest to being a Condorcet winner under a simple metric.
Llull's method and Copeland's method
| Candidate | Score |
|---|---|
| A | 1 |
| B | 2 |
| C | 0 |
Copeland's method assigns a score to each candidate derived from the results table, as shown above in the minimax section. The score is simply the number of favourable results in a candidate's row, i.e., the number of other candidates to whom a specific candidate is preferred by a majority of voters. The candidate with the highest score (in this case B) is the winner.
Copeland's method is Condorcet-consistent and straightforward, but for certain patterns of voter preferences (with no Condorcet winner), it will yield a tie regardless of the size of the electorate. Therefore, its proponents typically recommend its use in conjunction with a tie-breaker. Suitable rules for this purpose include minimax, IRV, and the Borda count, the latter giving rise to the Dasgupta–Maskin method.
Other methods
Several other voting methods provide alternatives to the methods described above, each with unique characteristics:
- Ranked voting: Different from cardinal voting, candidates are independently rated rather than ranked.[16]
- Condorcet completions: Elects the Condorcet winner if there is one and otherwise falls back on a separate procedure for determining the result. Examples include Black's method when using the Borda count as the fallback and the Nicolaus Tideman Condorcet-Hare when using IRV.[17]
- Bottom-two-runoff IRV or BTR-IRV: A Condorcet-consistent variant of IRV.
- Coombs' method: A variant of IRV where the candidate eliminated in each round has the most last-place preferences rather than the fewest first-place choices. Not Condorcet-consistent but satisfies the median voter theorem.[18]
- Baldwin's and Nanson's methods: Use more complicated elimination rules based on the Borda count. They are Condorcet-consistent.
- Kemeny–Young method: Complex but Condorcet-consistent.
- Smith's method: Reduces the set of candidates to the Smith set, which contains the Condorcet winner if there is one. Advocated for use with a tie-break, like IRV and minimax.[19]
- Bucklin's method: Exists in several forms, some of which are Condorcet-consistent.
- Ranked Pairs and Related Methods: The ranked pairs method – including the Schulze method, Schulze STV, and split cycle method – are Condorcet-consistent methods of medium computational complexity based on analyzing the cycle structure of ballots.[20]
- Dodgson's method: Devised by Lewis Carroll. It is Condorcet-consistent but computationally complex.
- Expanding approvals rule
See also
References
- ^ "Bill Status H.424: An act relating to town, city, and village elections for single-seat offices using ranked-choice voting". legislature.vermont.gov. Retrieved 2024-03-23.
Condorcet winner. If a candidate is the winning candidate in every paired comparison, the candidate shall be declared the winner of the election.
- ^ George G. Szpiro, "Numbers Rule" (2010).
- ^ Nanson, E. J. (1882). "Methods of election: Ware's Method". Transactions and Proceedings of the Royal Society of Victoria. 19: 206.
The method was, however, mentioned by Condorcet, but only to be condemned.
- ^ Condorcet, Jean-Antoine-Nicolas de Caritat (1788). "On the Constitution and the Functions of Provincial Assemblies". Complete Works of Condorcet (in French). Vol. 13 (published 1804). p. 243.
En effet, lorsqu'il y a plus de trois concurrents, le véritable vœu de la pluralité peut être pour un candidat qui n'ait eu aucune des voix dans le premier scrutin.
- ^ Duncan Black, "On the Rationale of Group Decision-making" (1948).
- ^ Farrell and McAllister, The Australian Electoral System, p. 17
- ^ "Ranked Choice Voting in Maine". legislature.maine.gov. State of Maine. 2022-08-23. Retrieved 2022-11-20.
- ^ Piper, Kelsey (2020-11-19). "Alaska voters adopt ranked-choice voting in ballot initiative". vox.com. Vox Media. Retrieved 2022-11-20.
- ^ "Ranked Choice Voting in Maine". Maine State Legislature. Retrieved 21 October 2021.
- ^ "Alaska Better Elections Implementation". Alaska Division of Elections. Retrieved 21 October 2021.
- ^ "New Zealand Cities Voting to Implement Ranked Choice Voting". 19 September 2017.
- ^ "Narodni skupnosti v prihodnje z enostavnejšim načinom izvolitve predstavnikov". Radio Koper - RTV Slovenija. 20 February 2021.
- ^ T. N. Tideman and F. Plassman, "Modeling the Outcomes of Vote-Casting in Actual Elections" (2012).
- ^ Alternative II.: Einführung einer Ersatzstimme (in German)
- ^ What is Dual Level Voting?
- ^ Riker, William Harrison (1982). Liberalism against populism: a confrontation between the theory of democracy and the theory of social choice. Waveland Pr. pp. 29–30. ISBN 0881333670. OCLC 316034736.
Ordinal utility is a measure of preferences in terms of rank orders—that is, first, second, etc. ... Cardinal utility is a measure of preferences on a scale of cardinal numbers, such as the scale from zero to one or the scale from one to ten.
- ^ J. Green-Armytage, T. N. Tideman and R. Cosman, "Statistical Evaluation of Voting Rules" (2015).
- ^ B. Grofman and S. L. Feld, "If you like the alternative vote (a.k.a. the instant runoff), then you ought to know about the Coombs rule" (2004)
- ^ R. B. Darlington, "Are Condorcet and Minimax Voting Systems the Best?" (v8, 2021).
- ^ W. H. Holliday and E. Pacuit, "Split Cycle: A New Condorcet Consistent Voting Method Independent of Clones and Immune to Spoilers" (2021).
External links
- Explainer video: How does ranked-choice voting work?, Minnesota Public Radio MPR.org
- Ballotpedia: "Ranked Choice Voting"
- Examples from RCV123.org
- FairVote.Org




