Polyhedral group

Selected point groups in three dimensions

Involutional symmetry Cs, (*) [ ] =	Cyclic symmetry Cnv, (*nn) [n] =	Dihedral symmetry Dnh, (*n22) [n,2] =
Polyhedral group, [n,3], (*n32)
Tetrahedral symmetry Td, (*332) [3,3] =	Octahedral symmetry Oh, (*432) [4,3] =	Icosahedral symmetry Ih, (*532) [5,3] =

In geometry, the polyhedral group is any of the symmetry groups of the Platonic solids.

Groups

There are three polyhedral groups:

• The tetrahedral group of order 12, rotational symmetry group of the regular tetrahedron. It is isomorphic to A₄.
  • The conjugacy classes of T are:
    • identity
    • 4 × rotation by 120°, order 3, cw
    • 4 × rotation by 120°, order 3, ccw
    • 3 × rotation by 180°, order 2
• The octahedral group of order 24, rotational symmetry group of the cube and the regular octahedron. It is isomorphic to S₄.
  • The conjugacy classes of O are:
    • identity
    • 6 × rotation by ±90° around vertices, order 4
    • 8 × rotation by ±120° around triangle centers, order 3
    • 3 × rotation by 180° around vertices, order 2
    • 6 × rotation by 180° around midpoints of edges, order 2
• The icosahedral group of order 60, rotational symmetry group of the regular dodecahedron and the regular icosahedron. It is isomorphic to A₅.
  • The conjugacy classes of I are:
    • identity
    • 12 × rotation by ±72°, order 5
    • 12 × rotation by ±144°, order 5
    • 20 × rotation by ±120°, order 3
    • 15 × rotation by 180°, order 2

These symmetries double to 24, 48, 120 respectively for the full reflectional groups. The reflection symmetries have 6, 9, and 15 mirrors respectively. The octahedral symmetry, [4,3] can be seen as the union of 6 tetrahedral symmetry [3,3] mirrors, and 3 mirrors of dihedral symmetry Dih₂, [2,2]. Pyritohedral symmetry is another doubling of tetrahedral symmetry.

The conjugacy classes of full tetrahedral symmetry, T_d ≅ S₄, are:

• identity
• 8 × rotation by 120°
• 3 × rotation by 180°
• 6 × reflection in a plane through two rotation axes
• 6 × rotoreflection by 90°

The conjugacy classes of pyritohedral symmetry, T_h, include those of T, with the two classes of 4 combined, and each with inversion:

• identity
• 8 × rotation by 120°
• 3 × rotation by 180°
• inversion
• 8 × rotoreflection by 60°
• 3 × reflection in a plane

The conjugacy classes of the full octahedral group, O_h ≅ S₄ × C₂, are:

• inversion
• 6 × rotoreflection by 90°
• 8 × rotoreflection by 60°
• 3 × reflection in a plane perpendicular to a 4-fold axis
• 6 × reflection in a plane perpendicular to a 2-fold axis

The conjugacy classes of full icosahedral symmetry, I_h ≅ A₅ × C₂, include also each with inversion:

• inversion
• 12 × rotoreflection by 108°, order 10
• 12 × rotoreflection by 36°, order 10
• 20 × rotoreflection by 60°, order 6
• 15 × reflection, order 2

Chiral polyhedral groups

Chiral polyhedral groups

Name (Orb.)	Coxeter notation	Order	Abstract structure	Rotation points #valence	Diagrams
					Orthogonal	Stereographic
T (332)	[3,3]+	12	A4	43 32
Th (3*2)	[4,3+]	24	A4 × C2	43 3*2
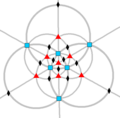
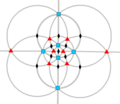
O (432)	[4,3]+	24	S4	34 43 62
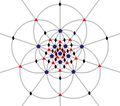
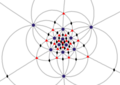
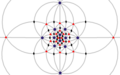
I (532)	[5,3]+	60	A5	65 103 152

Full polyhedral groups

Full polyhedral groups

Weyl Schoe. (Orb.)	Coxeter notation	Order	Abstract structure	Coxeter number (h)	Mirrors (m)	Mirror diagrams
						Orthogonal	Stereographic
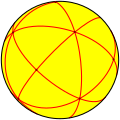
A3 Td (*332)	[3,3]	24	S4	4	6
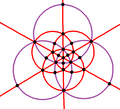
B3 Oh (*432)	[4,3]	48	S4 × C2	8	3 >6
H3 Ih (*532)	[5,3]	120	A5 × C2	10	15

See also

• Wythoff symbol
• List of spherical symmetry groups

References

• Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973. (The Polyhedral Groups. §3.5, pp. 46–47)

External links

• Weisstein, Eric W. "PolyhedralGroup". MathWorld.

This page was last edited on 9 March 2024, at 10:14