If the solution to a problem is easy to check for correctness, must the problem be easy to solve?
| Millennium Prize Problems |
|---|
The P versus NP problem is a major unsolved problem in theoretical computer science. Informally, it asks whether every problem whose solution can be quickly verified can also be quickly solved.
Here, quickly means an algorithm that solves the task and runs in polynomial time exists, meaning the task completion time varies as a polynomial function on the size of the input to the algorithm (as opposed to, say, exponential time). The general class of questions that some algorithm can answer in polynomial time is "P" or "class P". For some questions, there is no known way to find an answer quickly, but if provided with an answer, it can be verified quickly. The class of questions where an answer can be verified in polynomial time is NP, standing for "nondeterministic polynomial time".[Note 1]
An answer to the P versus NP question would determine whether problems that can be verified in polynomial time can also be solved in polynomial time. If P ≠ NP, which is widely believed, it would mean that there are problems in NP that are harder to compute than to verify: they could not be solved in polynomial time, but the answer could be verified in polynomial time.
The problem has been called the most important open problem in computer science.[1] Aside from being an important problem in computational theory, a proof either way would have profound implications for mathematics, cryptography, algorithm research, artificial intelligence, game theory, multimedia processing, philosophy, economics and many other fields.[2]
It is one of the seven Millennium Prize Problems selected by the Clay Mathematics Institute, each of which carries a US$1,000,000 prize for the first correct solution.
YouTube Encyclopedic
-
1/5Views:404 617921 162360 1323 357 32699 799
-
P vs. NP: The Biggest Puzzle in Computer Science
-
P vs. NP - The Biggest Unsolved Problem in Computer Science
-
16. Complexity: P, NP, NP-completeness, Reductions
-
P vs. NP and the Computational Complexity Zoo
-
P and NP - Georgia Tech - Computability, Complexity, Theory: Complexity
Transcription
Example
In the game Sudoku, the player begins with a partially filled-in grid of numbers and attempts to complete the grid following the game's rules. Given an incomplete Sudoku grid, of any size, is there at least one legal solution? Proposed solutions are easily verified, and the time to check a solution grows slowly (polynomially) as the grid gets bigger. However, all known algorithms for finding solutions take, for difficult examples, time that grows exponentially as the grid gets bigger. So, Sudoku is in NP (quickly checkable) but does not seem to be in P (quickly solvable). Thousands of other problems seem similarly fast to check but slow to solve. Researchers have shown that many of the problems in NP have the extra property that a fast solution to any one of them could be used to build a quick solution to any other problem in NP, a property called NP-completeness. Decades of searching have not produced a fast solution to any of these problems, so most scientists suspect that these problems cannot be solved quickly, however this is unproven.
History
The precise statement of the P versus NP problem was introduced in 1971 by Stephen Cook in his seminal paper "The complexity of theorem proving procedures"[3] (and independently by Leonid Levin in 1973[4]).
Although the P versus NP problem was formally defined in 1971, there were previous inklings of the problems involved, the difficulty of proof, and the potential consequences. In 1955, mathematician John Nash wrote a letter to the NSA, speculating that cracking a sufficiently complex code would require time exponential in the length of the key.[5] If proved (and Nash was suitably skeptical), this would imply what is now called P ≠ NP, since a proposed key can be verified in polynomial time. Another mention of the underlying problem occurred in a 1956 letter written by Kurt Gödel to John von Neumann. Gödel asked whether theorem-proving (now known to be co-NP-complete) could be solved in quadratic or linear time,[6] and pointed out one of the most important consequences—that if so, then the discovery of mathematical proofs could be automated.
Context
The relation between the complexity classes P and NP is studied in computational complexity theory, the part of the theory of computation dealing with the resources required during computation to solve a given problem. The most common resources are time (how many steps it takes to solve a problem) and space (how much memory it takes to solve a problem).
In such analysis, a model of the computer for which time must be analyzed is required. Typically such models assume that the computer is deterministic (given the computer's present state and any inputs, there is only one possible action that the computer might take) and sequential (it performs actions one after the other).
In this theory, the class P consists of all decision problems (defined below) solvable on a deterministic sequential machine in a duration polynomial in the size of the input; the class NP consists of all decision problems whose positive solutions are verifiable in polynomial time given the right information, or equivalently, whose solution can be found in polynomial time on a non-deterministic machine.[7] Clearly, P ⊆ NP. Arguably, the biggest open question in theoretical computer science concerns the relationship between those two classes:
- Is P equal to NP?
Since 2002, William Gasarch has conducted three polls of researchers concerning this and related questions.[8][9][10] Confidence that P ≠ NP has been increasing – in 2019, 88% believed P ≠ NP, as opposed to 83% in 2012 and 61% in 2002. When restricted to experts, the 2019 answers became 99% believed P ≠ NP.[10] These polls do not imply whether P = NP, Gasarch himself stated: "This does not bring us any closer to solving P=?NP or to knowing when it will be solved, but it attempts to be an objective report on the subjective opinion of this era."
NP-completeness
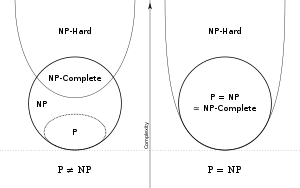
To attack the P = NP question, the concept of NP-completeness is very useful. NP-complete problems are problems that any other NP problem is reducible to in polynomial time and whose solution is still verifiable in polynomial time. That is, any NP problem can be transformed into any NP-complete problem. Informally, an NP-complete problem is an NP problem that is at least as "tough" as any other problem in NP.
NP-hard problems are those at least as hard as NP problems; i.e., all NP problems can be reduced (in polynomial time) to them. NP-hard problems need not be in NP; i.e., they need not have solutions verifiable in polynomial time.
For instance, the Boolean satisfiability problem is NP-complete by the Cook–Levin theorem, so any instance of any problem in NP can be transformed mechanically into a Boolean satisfiability problem in polynomial time. The Boolean satisfiability problem is one of many NP-complete problems. If any NP-complete problem is in P, then it would follow that P = NP. However, many important problems are NP-complete, and no fast algorithm for any of them is known.
From the definition alone it is unintuitive that NP-complete problems exist; however, a trivial NP-complete problem can be formulated as follows: given a Turing machine M guaranteed to halt in polynomial time, does a polynomial-size input that M will accept exist?[11] It is in NP because (given an input) it is simple to check whether M accepts the input by simulating M; it is NP-complete because the verifier for any particular instance of a problem in NP can be encoded as a polynomial-time machine M that takes the solution to be verified as input. Then the question of whether the instance is a yes or no instance is determined by whether a valid input exists.
The first natural problem proven to be NP-complete was the Boolean satisfiability problem, also known as SAT. As noted above, this is the Cook–Levin theorem; its proof that satisfiability is NP-complete contains technical details about Turing machines as they relate to the definition of NP. However, after this problem was proved to be NP-complete, proof by reduction provided a simpler way to show that many other problems are also NP-complete, including the game Sudoku discussed earlier. In this case, the proof shows that a solution of Sudoku in polynomial time could also be used to complete Latin squares in polynomial time.[12] This in turn gives a solution to the problem of partitioning tri-partite graphs into triangles,[13] which could then be used to find solutions for the special case of SAT known as 3-SAT,[14] which then provides a solution for general Boolean satisfiability. So a polynomial-time solution to Sudoku leads, by a series of mechanical transformations, to a polynomial time solution of satisfiability, which in turn can be used to solve any other NP-problem in polynomial time. Using transformations like this, a vast class of seemingly unrelated problems are all reducible to one another, and are in a sense "the same problem".
Harder problems
Although it is unknown whether P = NP, problems outside of P are known. Just as the class P is defined in terms of polynomial running time, the class EXPTIME is the set of all decision problems that have exponential running time. In other words, any problem in EXPTIME is solvable by a deterministic Turing machine in O(2p(n)) time, where p(n) is a polynomial function of n. A decision problem is EXPTIME-complete if it is in EXPTIME, and every problem in EXPTIME has a polynomial-time many-one reduction to it. A number of problems are known to be EXPTIME-complete. Because it can be shown that P ≠ EXPTIME, these problems are outside P, and so require more than polynomial time. In fact, by the time hierarchy theorem, they cannot be solved in significantly less than exponential time. Examples include finding a perfect strategy for chess positions on an N × N board[15] and similar problems for other board games.[16]
The problem of deciding the truth of a statement in Presburger arithmetic requires even more time. Fischer and Rabin proved in 1974[17] that every algorithm that decides the truth of Presburger statements of length n has a runtime of at least for some constant c. Hence, the problem is known to need more than exponential run time. Even more difficult are the undecidable problems, such as the halting problem. They cannot be completely solved by any algorithm, in the sense that for any particular algorithm there is at least one input for which that algorithm will not produce the right answer; it will either produce the wrong answer, finish without giving a conclusive answer, or otherwise run forever without producing any answer at all.
It is also possible to consider questions other than decision problems. One such class, consisting of counting problems, is called #P: whereas an NP problem asks "Are there any solutions?", the corresponding #P problem asks "How many solutions are there?". Clearly, a #P problem must be at least as hard as the corresponding NP problem, since a count of solutions immediately tells if at least one solution exists, if the count is greater than zero. Surprisingly, some #P problems that are believed to be difficult correspond to easy (for example linear-time) P problems.[18] For these problems, it is very easy to tell whether solutions exist, but thought to be very hard to tell how many. Many of these problems are #P-complete, and hence among the hardest problems in #P, since a polynomial time solution to any of them would allow a polynomial time solution to all other #P problems.
Problems in NP not known to be in P or NP-complete
In 1975, Richard E. Ladner showed that if P ≠ NP, then there exist problems in NP that are neither in P nor NP-complete.[19] Such problems are called NP-intermediate problems. The graph isomorphism problem, the discrete logarithm problem, and the integer factorization problem are examples of problems believed to be NP-intermediate. They are some of the very few NP problems not known to be in P or to be NP-complete.
The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic. An important unsolved problem in complexity theory is whether the graph isomorphism problem is in P, NP-complete, or NP-intermediate. The answer is not known, but it is believed that the problem is at least not NP-complete.[20] If graph isomorphism is NP-complete, the polynomial time hierarchy collapses to its second level.[21] Since it is widely believed that the polynomial hierarchy does not collapse to any finite level, it is believed that graph isomorphism is not NP-complete. The best algorithm for this problem, due to László Babai, runs in quasi-polynomial time.[22]
The integer factorization problem is the computational problem of determining the prime factorization of a given integer. Phrased as a decision problem, it is the problem of deciding whether the input has a factor less than k. No efficient integer factorization algorithm is known, and this fact forms the basis of several modern cryptographic systems, such as the RSA algorithm. The integer factorization problem is in NP and in co-NP (and even in UP and co-UP[23]). If the problem is NP-complete, the polynomial time hierarchy will collapse to its first level (i.e., NP = co-NP). The most efficient known algorithm for integer factorization is the general number field sieve, which takes expected time
to factor an n-bit integer. The best known quantum algorithm for this problem, Shor's algorithm, runs in polynomial time, although this does not indicate where the problem lies with respect to non-quantum complexity classes.
Does P mean "easy"?
All of the above discussion has assumed that P means "easy" and "not in P" means "difficult", an assumption known as Cobham's thesis. It is a common and reasonably accurate [citation needed] assumption in complexity theory; but there are caveats.
First, it can be false in practice. A theoretical polynomial algorithm may have extremely large constant factors or exponents, rendering it impractical. For example, the problem of deciding whether a graph G contains H as a minor, where H is fixed, can be solved in a running time of O(n2),[25] where n is the number of vertices in G. However, the big O notation hides a constant that depends tetrationally on H. The constant is greater than (using Knuth's up-arrow notation), and where h is the number of vertices in H.[26]
On the other hand, even if a problem is shown to be NP-complete, and even if P ≠ NP, there may still be effective approaches to the problem in practice. There are algorithms for many NP-complete problems, such as the knapsack problem, the traveling salesman problem, and the Boolean satisfiability problem, that can solve to optimality many real-world instances in reasonable time. The empirical average-case complexity (time vs. problem size) of such algorithms can be surprisingly low. An example is the simplex algorithm in linear programming, which works surprisingly well in practice; despite having exponential worst-case time complexity, it runs on par with the best known polynomial-time algorithms.[27]
Finally, there are types of computations which do not conform to the Turing machine model on which P and NP are defined, such as quantum computation and randomized algorithms.
Reasons to believe P ≠ NP or P = NP
Cook provides a restatement of the problem in The P Versus NP Problem as "Does P = NP?"[28] According to polls,[8][29] most computer scientists believe that P ≠ NP. A key reason for this belief is that after decades of studying these problems no one has been able to find a polynomial-time algorithm for any of more than 3000 important known NP-complete problems (see List of NP-complete problems). These algorithms were sought long before the concept of NP-completeness was even defined (Karp's 21 NP-complete problems, among the first found, were all well-known existing problems at the time they were shown to be NP-complete). Furthermore, the result P = NP would imply many other startling results that are currently believed to be false, such as NP = co-NP and P = PH.
It is also intuitively argued that the existence of problems that are hard to solve but for which the solutions are easy to verify matches real-world experience.[30]
If P = NP, then the world would be a profoundly different place than we usually assume it to be. There would be no special value in "creative leaps", no fundamental gap between solving a problem and recognizing the solution once it's found.
On the other hand, some researchers believe that there is overconfidence in believing P ≠ NP and that researchers should explore proofs of P = NP as well. For example, in 2002 these statements were made:[8]
The main argument in favor of P ≠ NP is the total lack of fundamental progress in the area of exhaustive search. This is, in my opinion, a very weak argument. The space of algorithms is very large and we are only at the beginning of its exploration. [...] The resolution of Fermat's Last Theorem also shows that very simple questions may be settled only by very deep theories.
Being attached to a speculation is not a good guide to research planning. One should always try both directions of every problem. Prejudice has caused famous mathematicians to fail to solve famous problems whose solution was opposite to their expectations, even though they had developed all the methods required.
DLIN vs NLIN
When one substitutes "linear time on a multitape Turing machine" for "polynomial time" in the definitions of P and NP, one obtains the classes DLIN and NLIN. It is known[31] that DLIN≠NLIN.
Consequences of solution
One of the reasons the problem attracts so much attention is the consequences of the possible answers. Either direction of resolution would advance theory enormously, and perhaps have huge practical consequences as well.
P = NP
A proof that P = NP could have stunning practical consequences if the proof leads to efficient methods for solving some of the important problems in NP. The potential consequences, both positive and negative, arise since various NP-complete problems are fundamental in many fields.
It is also very possible that a proof would not lead to practical algorithms for NP-complete problems. The formulation of the problem does not require that the bounding polynomial be small or even specifically known. A non-constructive proof might show a solution exists without specifying either an algorithm to obtain it or a specific bound. Even if the proof is constructive, showing an explicit bounding polynomial and algorithmic details, if the polynomial is not very low-order the algorithm might not be sufficiently efficient in practice. In this case the initial proof would be mainly of interest to theoreticians, but the knowledge that polynomial time solutions are possible would surely spur research into better (and possibly practical) methods to achieve them.
A solution showing P = NP could upend the field of cryptography, which relies on certain problems being difficult. A constructive and efficient solution[Note 2] to an NP-complete problem such as 3-SAT would break most existing cryptosystems including:
- Existing implementations of public-key cryptography,[32] a foundation for many modern security applications such as secure financial transactions over the Internet.
- Symmetric ciphers such as AES or 3DES,[33] used for the encryption of communications data.
- Cryptographic hashing, which underlies blockchain cryptocurrencies such as Bitcoin, and is used to authenticate software updates. For these applications, finding a pre-image that hashes to a given value must be difficult, ideally taking exponential time. If P = NP, then this can take polynomial time, through reduction to SAT.[34]
These would need modification or replacement with information-theoretically secure solutions that do not assume P ≠ NP.
There are also enormous benefits that would follow from rendering tractable many currently mathematically intractable problems. For instance, many problems in operations research are NP-complete, such as types of integer programming and the travelling salesman problem. Efficient solutions to these problems would have enormous implications for logistics. Many other important problems, such as some problems in protein structure prediction, are also NP-complete;[35] making these problems efficiently solvable could considerably advance life sciences and biotechnology.
These changes could be insignificant compared to the revolution efficiently solving NP-complete problems would cause in mathematics itself. Gödel, in his early thoughts on computational complexity, noted that a mechanical method that could solve any problem would revolutionize mathematics:[36][37]
If there really were a machine with φ(n) ∼ k⋅n (or even ∼ k⋅n2), this would have consequences of the greatest importance. Namely, it would obviously mean that in spite of the undecidability of the Entscheidungsproblem, the mental work of a mathematician concerning Yes-or-No questions could be completely replaced by a machine. After all, one would simply have to choose the natural number n so large that when the machine does not deliver a result, it makes no sense to think more about the problem.
Similarly, Stephen Cook (assuming not only a proof, but a practically efficient algorithm) says:[28]
... it would transform mathematics by allowing a computer to find a formal proof of any theorem which has a proof of a reasonable length, since formal proofs can easily be recognized in polynomial time. Example problems may well include all of the CMI prize problems.
Research mathematicians spend their careers trying to prove theorems, and some proofs have taken decades or even centuries to find after problems have been stated—for instance, Fermat's Last Theorem took over three centuries to prove. A method guaranteed to find a proof if a "reasonable" size proof exists, would essentially end this struggle.
Donald Knuth has stated that he has come to believe that P = NP, but is reserved about the impact of a possible proof:[38]
[...] if you imagine a number M that's finite but incredibly large—like say the number 10↑↑↑↑3 discussed in my paper on "coping with finiteness"—then there's a humongous number of possible algorithms that do nM bitwise or addition or shift operations on n given bits, and it's really hard to believe that all of those algorithms fail. My main point, however, is that I don't believe that the equality P = NP will turn out to be helpful even if it is proved, because such a proof will almost surely be nonconstructive.
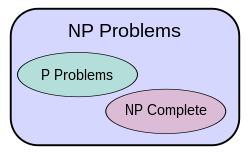
P ≠ NP
A proof of P ≠ NP would lack the practical computational benefits of a proof that P = NP, but would represent a great advance in computational complexity theory and guide future research. It would demonstrate that many common problems cannot be solved efficiently, so that the attention of researchers can be focused on partial solutions or solutions to other problems. Due to widespread belief in P ≠ NP, much of this focusing of research has already taken place.[39]
P ≠ NP still leaves open the average-case complexity of hard problems in NP. For example, it is possible that SAT requires exponential time in the worst case, but that almost all randomly selected instances of it are efficiently solvable. Russell Impagliazzo has described five hypothetical "worlds" that could result from different possible resolutions to the average-case complexity question.[40] These range from "Algorithmica", where P = NP and problems like SAT can be solved efficiently in all instances, to "Cryptomania", where P ≠ NP and generating hard instances of problems outside P is easy, with three intermediate possibilities reflecting different possible distributions of difficulty over instances of NP-hard problems. The "world" where P ≠ NP but all problems in NP are tractable in the average case is called "Heuristica" in the paper. A Princeton University workshop in 2009 studied the status of the five worlds.[41]
Results about difficulty of proof
Although the P = NP problem itself remains open despite a million-dollar prize and a huge amount of dedicated research, efforts to solve the problem have led to several new techniques. In particular, some of the most fruitful research related to the P = NP problem has been in showing that existing proof techniques are insufficient for answering the question, suggesting novel technical approaches are required.
As additional evidence for the difficulty of the problem, essentially all known proof techniques in computational complexity theory fall into one of the following classifications, all insufficient to prove P ≠ NP:
| Classification | Definition |
|---|---|
| Relativizing proofs | Imagine a world where every algorithm is allowed to make queries to some fixed subroutine called an oracle (which can answer a fixed set of questions in constant time, such as an oracle that solves any traveling salesman problem in 1 step), and the running time of the oracle is not counted against the running time of the algorithm. Most proofs (especially classical ones) apply uniformly in a world with oracles regardless of what the oracle does. These proofs are called relativizing. In 1975, Baker, Gill, and Solovay showed that P = NP with respect to some oracles, while P ≠ NP for other oracles.[42] As relativizing proofs can only prove statements that are true for all possible oracles, these techniques cannot resolve P = NP. |
| Natural proofs | In 1993, Alexander Razborov and Steven Rudich defined a general class of proof techniques for circuit complexity lower bounds, called natural proofs.[43] At the time, all previously known circuit lower bounds were natural, and circuit complexity was considered a very promising approach for resolving P = NP. However, Razborov and Rudich showed that if one-way functions exist, P and NP are indistinguishable to natural proof methods. Although the existence of one-way functions is unproven, most mathematicians believe that they do, and a proof of their existence would be a much stronger statement than P ≠ NP. Thus it is unlikely that natural proofs alone can resolve P = NP. |
| Algebrizing proofs | After the Baker–Gill–Solovay result, new non-relativizing proof techniques were successfully used to prove that IP = PSPACE. However, in 2008, Scott Aaronson and Avi Wigderson showed that the main technical tool used in the IP = PSPACE proof, known as arithmetization, was also insufficient to resolve P = NP.[44] Arithmetization converts the operations of an algorithm to algebraic and basic arithmetic symbols and then uses those to analyze the workings. In the IP = PSPACE proof, they convert the black box and the Boolean circuits to an algebraic problem.[44] As mentioned previously, it has proven that this method is not viable to solve P = NP and other time complexity problems. |
These barriers are another reason why NP-complete problems are useful: if a polynomial-time algorithm can be demonstrated for an NP-complete problem, this would solve the P = NP problem in a way not excluded by the above results.
These barriers lead some computer scientists to suggest the P versus NP problem may be independent of standard axiom systems like ZFC (cannot be proved or disproved within them). An independence result could imply that either P ≠ NP and this is unprovable in (e.g.) ZFC, or that P = NP but it is unprovable in ZFC that any polynomial-time algorithms are correct.[45] However, if the problem is undecidable even with much weaker assumptions extending the Peano axioms for integer arithmetic, then nearly polynomial-time algorithms exist for all NP problems.[46] Therefore, assuming (as most complexity theorists do) some NP problems don't have efficient algorithms, proofs of independence with those techniques are impossible. This also implies proving independence from PA or ZFC with current techniques is no easier than proving all NP problems have efficient algorithms.
Logical characterizations
The P = NP problem can be restated as certain classes of logical statements, as a result of work in descriptive complexity.
Consider all languages of finite structures with a fixed signature including a linear order relation. Then, all such languages in P are expressible in first-order logic with the addition of a suitable least fixed-point combinator. Recursive functions can be defined with this and the order relation. As long as the signature contains at least one predicate or function in addition to the distinguished order relation, so that the amount of space taken to store such finite structures is actually polynomial in the number of elements in the structure, this precisely characterizes P.
Similarly, NP is the set of languages expressible in existential second-order logic—that is, second-order logic restricted to exclude universal quantification over relations, functions, and subsets. The languages in the polynomial hierarchy, PH, correspond to all of second-order logic. Thus, the question "is P a proper subset of NP" can be reformulated as "is existential second-order logic able to describe languages (of finite linearly ordered structures with nontrivial signature) that first-order logic with least fixed point cannot?".[47] The word "existential" can even be dropped from the previous characterization, since P = NP if and only if P = PH (as the former would establish that NP = co-NP, which in turn implies that NP = PH).
Polynomial-time algorithms
No known algorithm for a NP-complete problem runs in polynomial time. However, there are algorithms known for NP-complete problems that if P = NP, the algorithm runs in polynomial time on accepting instances (although with enormous constants, making the algorithm impractical). However, these algorithms do not qualify as polynomial time because their running time on rejecting instances are not polynomial. The following algorithm, due to Levin (without any citation), is such an example below. It correctly accepts the NP-complete language SUBSET-SUM. It runs in polynomial time on inputs that are in SUBSET-SUM if and only if P = NP:
// Algorithm that accepts the NP-complete language SUBSET-SUM.
//
// this is a polynomial-time algorithm if and only if P = NP.
//
// "Polynomial-time" means it returns "yes" in polynomial time when
// the answer should be "yes", and runs forever when it is "no".
//
// Input: S = a finite set of integers
// Output: "yes" if any subset of S adds up to 0.
// Runs forever with no output otherwise.
// Note: "Program number M" is the program obtained by
// writing the integer M in binary, then
// considering that string of bits to be a
// program. Every possible program can be
// generated this way, though most do nothing
// because of syntax errors.
FOR K = 1...∞
FOR M = 1...K
Run program number M for K steps with input S
IF the program outputs a list of distinct integers
AND the integers are all in S
AND the integers sum to 0
THEN
OUTPUT "yes" and HALT
This is a polynomial-time algorithm accepting an NP-complete language only if P = NP. "Accepting" means it gives "yes" answers in polynomial time, but is allowed to run forever when the answer is "no" (also known as a semi-algorithm).
This algorithm is enormously impractical, even if P = NP. If the shortest program that can solve SUBSET-SUM in polynomial time is b bits long, the above algorithm will try at least 2b − 1 other programs first.
Formal definitions
P and NP
A decision problem is a problem that takes as input some string w over an alphabet Σ, and outputs "yes" or "no". If there is an algorithm (say a Turing machine, or a computer program with unbounded memory) that produces the correct answer for any input string of length n in at most cnk steps, where k and c are constants independent of the input string, then we say that the problem can be solved in polynomial time and we place it in the class P. Formally, P is the set of languages that can be decided by a deterministic polynomial-time Turing machine. Meaning,
where
and a deterministic polynomial-time Turing machine is a deterministic Turing machine M that satisfies two conditions:
- M halts on all inputs w and
- there exists such that , where O refers to the big O notation and
NP can be defined similarly using nondeterministic Turing machines (the traditional way). However, a modern approach uses the concept of certificate and verifier. Formally, NP is the set of languages with a finite alphabet and verifier that runs in polynomial time. The following defines a "verifier":
Let L be a language over a finite alphabet, Σ.
L ∈ NP if, and only if, there exists a binary relation and a positive integer k such that the following two conditions are satisfied:
- For all , such that (x, y) ∈ R and ; and
- the language over is decidable by a deterministic Turing machine in polynomial time.
A Turing machine that decides LR is called a verifier for L and a y such that (x, y) ∈ R is called a certificate of membership of x in L.
Not all verifiers must be polynomial-time. However, for L to be in NP, there must be a verifier that runs in polynomial time.
Example
Let
Whether a value of x is composite is equivalent to of whether x is a member of COMPOSITE. It can be shown that COMPOSITE ∈ NP by verifying that it satisfies the above definition (if we identify natural numbers with their binary representations).
COMPOSITE also happens to be in P, a fact demonstrated by the invention of the AKS primality test.[48]
NP-completeness
There are many equivalent ways of describing NP-completeness.
Let L be a language over a finite alphabet Σ.
L is NP-complete if, and only if, the following two conditions are satisfied:
- L ∈ NP; and
- any L' in NP is polynomial-time-reducible to L (written as ), where if, and only if, the following two conditions are satisfied:
- There exists f : Σ* → Σ* such that for all w in Σ* we have: ; and
- there exists a polynomial-time Turing machine that halts with f(w) on its tape on any input w.
Alternatively, if L ∈ NP, and there is another NP-complete problem that can be polynomial-time reduced to L, then L is NP-complete. This is a common way of proving some new problem is NP-complete.
Claimed solutions
While the P versus NP problem is generally considered unsolved,[49] many amateur and some professional researchers have claimed solutions. Gerhard J. Woeginger compiled a list of 62 purported proofs of P = NP from 1986 to 2016, of which 50 were proofs of P ≠ NP, 2 were proofs the problem is unprovable, and one was a proof that it is undecidable.[50] Some attempts at resolving P versus NP have received brief media attention,[51] though these attempts have been refuted.
Popular culture
The film Travelling Salesman, by director Timothy Lanzone, is the story of four mathematicians hired by the US government to solve the P versus NP problem.[52]
In the sixth episode of The Simpsons' seventh season "Treehouse of Horror VI", the equation P = NP is seen shortly after Homer accidentally stumbles into the "third dimension".[53][54]
In the second episode of season 2 of Elementary, "Solve for X" Sherlock and Watson investigate the murders of mathematicians who were attempting to solve P versus NP.[55][56]
See also
- Game complexity
- List of unsolved problems in mathematics
- Unique games conjecture
- Unsolved problems in computer science
Notes
- ^ A nondeterministic Turing machine can move to a state that is not determined by the previous state. Such a machine could solve an NP problem in polynomial time by falling into the correct answer state (by luck), then conventionally verifying it. Such machines are not practical for solving realistic problems but can be used as theoretical models.
- ^ Exactly how efficient a solution must be to pose a threat to cryptography depends on the details. A solution of with a reasonable constant term would be disastrous. On the other hand, a solution that is in almost all cases would not pose an immediate practical danger.
References
- ^ Fortnow, Lance (2009). "The status of the P versus NP problem" (PDF). Communications of the ACM. 52 (9): 78–86. CiteSeerX 10.1.1.156.767. doi:10.1145/1562164.1562186. S2CID 5969255. Archived from the original (PDF) on 24 February 2011. Retrieved 26 January 2010.
- ^ Fortnow, Lance (2013). The Golden Ticket: P, NP, and the Search for the Impossible. Princeton, NJ: Princeton University Press. ISBN 9780691156491.
- ^ Cook, Stephen (1971). "The complexity of theorem proving procedures". Proceedings of the Third Annual ACM Symposium on Theory of Computing. pp. 151–158. doi:10.1145/800157.805047. ISBN 9781450374644. S2CID 7573663.
- ^ L. A. Levin (1973). Универсальные задачи перебора [Problems of Information Transmission]. Пробл. передачи информ (in Russian). 9 (3): 115–116.
- ^ NSA (2012). "Letters from John Nash" (PDF). Archived (PDF) from the original on 9 November 2018.
- ^ Hartmanis, Juris. "Gödel, von Neumann, and the P = NP problem" (PDF). Bulletin of the European Association for Theoretical Computer Science. 38: 101–107.
- ^ Sipser, Michael: Introduction to the Theory of Computation, Second Edition, International Edition, page 270. Thomson Course Technology, 2006. Definition 7.19 and Theorem 7.20.
- ^ a b c William I. Gasarch (June 2002). "The P=?NP poll" (PDF). SIGACT News. 33 (2): 34–47. CiteSeerX 10.1.1.172.1005. doi:10.1145/564585.564599. S2CID 36828694. Archived (PDF) from the original on 15 June 2007.
- ^ William I. Gasarch. "The Second P=?NP poll" (PDF). SIGACT News. 74. Archived (PDF) from the original on 24 January 2014.
- ^ a b "Guest Column: The Third P =? NP Poll1" (PDF). Archived (PDF) from the original on 31 March 2019. Retrieved 25 May 2020.
- ^ Scott Aaronson. "PHYS771 Lecture 6: P, NP, and Friends". Retrieved 27 August 2007.
- ^ "MSc course: Foundations of Computer Science". www.cs.ox.ac.uk. Retrieved 25 May 2020.
- ^ Colbourn, Charles J. (1984). "The complexity of completing partial Latin squares". Discrete Applied Mathematics. 8 (1): 25–30. doi:10.1016/0166-218X(84)90075-1.
- ^ I. Holyer (1981). "The NP-completeness of some edge-partition problems". SIAM J. Comput. 10 (4): 713–717. doi:10.1137/0210054.
- ^ Aviezri Fraenkel and D. Lichtenstein (1981). "Computing a perfect strategy for n × n chess requires time exponential in n". Journal of Combinatorial Theory. Series A. 31 (2): 199–214. doi:10.1016/0097-3165(81)90016-9.
- ^ David Eppstein. "Computational Complexity of Games and Puzzles".
- ^ Fischer, Michael J.; Rabin, Michael O. (1974). "Super-Exponential Complexity of Presburger Arithmetic". Proceedings of the SIAM-AMS Symposium in Applied Mathematics. 7: 27–41. Archived from the original on 15 September 2006. Retrieved 15 October 2017.
- ^ Valiant, Leslie G. (1979). "The complexity of enumeration and reliability problems". SIAM Journal on Computing. 8 (3): 410–421. doi:10.1137/0208032.
- ^ a b Ladner, R.E. (1975). "On the structure of polynomial time reducibility". Journal of the ACM. 22: 151–171 See Corollary 1.1. doi:10.1145/321864.321877. S2CID 14352974.
- ^ Arvind, Vikraman; Kurur, Piyush P. (2006). "Graph isomorphism is in SPP". Information and Computation. 204 (5): 835–852. doi:10.1016/j.ic.2006.02.002.
- ^ Schöning, Uwe (1988). "Graph isomorphism is in the low hierarchy". Journal of Computer and System Sciences. 37 (3): 312–323. doi:10.1016/0022-0000(88)90010-4.
- ^ Babai, László (2018). "Group, graphs, algorithms: the graph isomorphism problem". Proceedings of the International Congress of Mathematicians—Rio de Janeiro 2018. Vol. IV. Invited lectures. World Sci. Publ., Hackensack, NJ. pp. 3319–3336. MR 3966534.
- ^ Lance Fortnow. Computational Complexity Blog: Complexity Class of the Week: Factoring. 13 September 2002.
- ^ Pisinger, D. 2003. "Where are the hard knapsack problems?" Technical Report 2003/08, Department of Computer Science, University of Copenhagen, Copenhagen, Denmark
- ^ Kawarabayashi, Ken-ichi; Kobayashi, Yusuke; Reed, Bruce (2012). "The disjoint paths problem in quadratic time". Journal of Combinatorial Theory. Series B. 102 (2): 424–435. doi:10.1016/j.jctb.2011.07.004.
- ^ Johnson, David S. (1987). "The NP-completeness column: An ongoing guide (edition 19)". Journal of Algorithms. 8 (2): 285–303. CiteSeerX 10.1.1.114.3864. doi:10.1016/0196-6774(87)90043-5.
- ^ Gondzio, Jacek; Terlaky, Tamás (1996). "3 A computational view of interior point methods". In J. E. Beasley (ed.). Advances in linear and integer programming. Oxford Lecture Series in Mathematics and its Applications. Vol. 4. New York: Oxford University Press. pp. 103–144. MR 1438311. Postscript file at website of Gondzio and at McMaster University website of Terlaky.
- ^ a b Cook, Stephen (April 2000). "The P versus NP Problem" (PDF). Clay Mathematics Institute. Archived (PDF) from the original on 16 December 2013. Retrieved 18 October 2006.
- ^ Rosenberger, Jack (May 2012). "P vs. NP poll results". Communications of the ACM. 55 (5): 10.
- ^ Scott Aaronson (4 September 2006). "Reasons to believe"., point 9.
- ^ Balcazar, Jose Luis; Diaz, Josep; Gabarro, Joaquim (1990). Structural Complexity II. Springer Verlag. ISBN 3-540-52079-1., Theorem 3.9
- ^ See Horie, S.; Watanabe, O. (1997). "Hard instance generation for SAT". Algorithms and Computation. Lecture Notes in Computer Science. Vol. 1350. Springer. pp. 22–31. arXiv:cs/9809117. Bibcode:1998cs........9117H. doi:10.1007/3-540-63890-3_4. ISBN 978-3-540-63890-2. for a reduction of factoring to SAT. A 512-bit factoring problem (8400 MIPS-years when factored) translates to a SAT problem of 63,652 variables and 406,860 clauses.
- ^ See, for example, Massacci, F.; Marraro, L. (2000). "Logical cryptanalysis as a SAT problem". Journal of Automated Reasoning. 24 (1): 165–203. CiteSeerX 10.1.1.104.962. doi:10.1023/A:1006326723002. S2CID 3114247. in which an instance of DES is encoded as a SAT problem with 10336 variables and 61935 clauses. A 3DES problem instance would be about 3 times this size.
- ^ De, Debapratim; Kumarasubramanian, Abishek; Venkatesan, Ramarathnam (2007). "Inversion attacks on secure hash functions using SAT solvers". Theory and Applications of Satisfiability Testing – SAT 2007. International Conference on Theory and Applications of Satisfiability Testing. Springer. pp. 377–382. doi:10.1007/978-3-540-72788-0_36.
- ^ Berger, B.; Leighton, T. (1998). "Protein folding in the hydrophobic-hydrophilic (HP) model is NP-complete". J. Comput. Biol. 5 (1): 27–40. CiteSeerX 10.1.1.139.5547. doi:10.1089/cmb.1998.5.27. PMID 9541869.
- ^ History of this letter and its translation from Sipser, Michael. "The History and Status of the P versus NP question" (PDF). Archived (PDF) from the original on 2 February 2014.
- ^ Johnson, David S. (August 2012). "A Brief History of NP-Completeness, 1954–2012". In Grötschel, M. (ed.). Optimization Stories (PDF). Documenta Mathematica. pp. 359–376. ISBN 978-3-936609-58-5. ISSN 1431-0643.
- ^ Knuth, Donald E. (20 May 2014). Twenty Questions for Donald Knuth. InformIT. Retrieved 20 July 2014.
- ^ L. R. Foulds (October 1983). "The Heuristic Problem-Solving Approach". Journal of the Operational Research Society. 34 (10): 927–934. doi:10.2307/2580891. JSTOR 2580891.
- ^ R. Impagliazzo, "A personal view of average-case complexity", p. 134, 10th Annual Structure in Complexity Theory Conference (SCT'95), 1995.
- ^ "Tentative program for the workshop on "Complexity and Cryptography: Status of Impagliazzo's Worlds"". Archived from the original on 15 November 2013.
- ^ T. P. Baker; J. Gill; R. Solovay (1975). "Relativizations of the P =? NP Question". SIAM Journal on Computing. 4 (4): 431–442. doi:10.1137/0204037.
- ^ Razborov, Alexander A.; Steven Rudich (1997). "Natural proofs". Journal of Computer and System Sciences. 55 (1): 24–35. doi:10.1006/jcss.1997.1494.
- ^ a b S. Aaronson; A. Wigderson (2008). Algebrization: A New Barrier in Complexity Theory (PDF). Proceedings of ACM STOC'2008. pp. 731–740. doi:10.1145/1374376.1374481. Archived (PDF) from the original on 21 February 2008.
- ^ Aaronson, Scott. "Is P Versus NP Formally Independent?" (PDF). Archived (PDF) from the original on 16 January 2017..
- ^ Ben-David, Shai; Halevi, Shai (1992). On the independence of P versus NP. Technion (Technical report). Vol. 714. Archived from the original (GZIP) on 2 March 2012..
- ^ Elvira Mayordomo. "P versus NP" Archived 16 February 2012 at the Wayback Machine Monografías de la Real Academia de Ciencias de Zaragoza 26: 57–68 (2004).
- ^ Agrawal, Manindra; Kayal, Neeraj; Saxena, Nitin (2004). "PRIMES is in P" (PDF). Annals of Mathematics. 160 (2): 781–793. doi:10.4007/annals.2004.160.781. JSTOR 3597229. Archived (PDF) from the original on 26 September 2006.
- ^ John Markoff (8 October 2009). "Prizes Aside, the P-NP Puzzler Has Consequences". The New York Times.
- ^ Gerhard J. Woeginger. "The P-versus-NP page". Retrieved 24 June 2018.
- ^ Markoff, John (16 August 2010). "Step 1: Post Elusive Proof. Step 2: Watch Fireworks". The New York Times. Retrieved 20 September 2010.
- ^ Geere, Duncan (26 April 2012). "'Travelling Salesman' movie considers the repercussions if P equals NP". Wired UK. Retrieved 26 April 2012.
- ^ Hardesty, Larry (29 October 2009). "Explained: P vs. NP".
- ^ Shadia, Ajam (13 September 2013). "What is the P vs. NP problem? Why is it important?".
- ^ Gasarch, William (7 October 2013). "P vs NP is Elementary? No— P vs NP is ON Elementary". blog.computationalcomplexity.org. Retrieved 6 July 2018.
- ^ Kirkpatrick, Noel (4 October 2013). "Elementary Solve for X Review: Sines of Murder". TV.com. Retrieved 6 July 2018.
Sources
- Rachel Crowell (28 May 2021). "The Top Unsolved Questions in Mathematics Remain Mostly Mysterious Just one of the seven Millennium Prize Problems named 21 years ago has been solved". www.scientificamerican.com. Retrieved 21 June 2021.
This problem concerns the issue of whether questions that are easy to verify (a class of queries called NP) also have solutions that are easy to find (a class called P).
- Hosch, William L (11 August 2009). "P versus NP problem mathematics". Encyclopædia Britannica. Retrieved 20 June 2021.
- "P vs NP Problem". www.claymath.org (Cook, Levin). Retrieved 20 June 2021.
Suppose that you are organizing housing accommodations for a group of four hundred university students. Space is limited and only one hundred of the students will receive places in the dormitory. To complicate matters, the Dean has provided you with a list of pairs of incompatible students, and requested that no pair from this list appear in your final choice. This is an example of what computer scientists call an NP-problem...
Further reading
- Cormen, Thomas (2001). Introduction to Algorithms. Cambridge: MIT Press. ISBN 978-0-262-03293-3.
- Garey, Michael R.; Johnson, David S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. Series of Books in the Mathematical Sciences (1st ed.). New York: W. H. Freeman and Company. ISBN 9780716710455. MR 0519066. OCLC 247570676.
- Goldreich, Oded (2010). P, NP, and NP-Completeness. Cambridge: Cambridge University Press. ISBN 978-0-521-12254-2. Online drafts
- Immerman, Neil (1987). "Languages that Capture Complexity Classes". SIAM Journal on Computing. 16 (4): 760–778. CiteSeerX 10.1.1.75.3035. doi:10.1137/0216051.
- Papadimitriou, Christos (1994). Computational Complexity. Boston: Addison-Wesley. ISBN 978-0-201-53082-7.
External links
- Fortnow, L.; Gasarch, W. "Computational complexity".
- Aviad Rubinstein's Hardness of Approximation Between P and NP, winner of the ACM's 2017 Doctoral Dissertation Award.
- "P vs. NP and the Computational Complexity Zoo". 26 August 2014. Archived from the original on 24 November 2021 – via YouTube.





















