| Order-7 heptagonal tiling | |
|---|---|
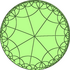
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic regular tiling |
| Vertex configuration | 77 |
| Schläfli symbol | {7,7} |
| Wythoff symbol | 7 | 7 2 |
| Coxeter diagram | |
| Symmetry group | [7,7], (*772) |
| Dual | self dual |
| Properties | Vertex-transitive, edge-transitive, face-transitive |
In geometry, the order-7 heptagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {7,7}, constructed from seven heptagons around every vertex. As such, it is self-dual.
YouTube Encyclopedic
-
1/5Views:135 54091 1593371 2482 566
-
Reflection Symmetry and Rotational Symmetry 128-2.7
-
Rotational Symmetry
-
Recursively Defined Partial Tilings of the Plane
-
How can you lift an elephant with one hand ?
-
SpiderBot - Building the Cannon in ZBrush Part 01 (Full Tutorial at BadKing.com.au)
Transcription
This video is provided as supplementary material for courses taught at Howard Community College and in this video I'm going to talk about two kinds of symmetric, reflection symmetry and rotational symmetry. Let's start with reflection symmetry. Reflection symmetry is sometimes called line symmetry or mirror symmetry and here's what it's about. I've drawn a picture of a heart and I'm going to draw a dotted line right at the center of it. Now that the dotted line divides the image into two mirror images of each other, or two reflections. The line itself is called the line of symmetry. So anytime you can take an image and draw a line through it so that you've got a pair of mirror images, you've got what's called reflection symmetry. Another way of thinking of reflection symmetry would be, if you had, as I have here, a cut-out of that image. If I take this heart, this cut-out that I have, and fold it along the line of symmetry, both sides will match up perfectly. So that's another way of seeing what reflection symmetry is about. Now you can have more than one line of symmetry. Here I've got a diamond. If I draw a dotted line, a long one to connect two opposite angles, I'm going to create two mirror images. On the other hand, I could have drawn a dotted line, a shorter one, connecting the other two opposite angles, and that would also create a mirror image. If I do this with paper, I can fold this paper one way and both sites will match, or I can fold the paper the other way and both sides will match. So you can have more than one line of symmetry. If you had a pentagon, you'd have five lines of symmetry. So you could have a number of lines of symmetry . So that's what reflection symmetry is about. Then we've got something called rotational symmetry. So to demonstrate rotational symmetry I've drawn a triangle and I've cut out a triangle that's the same size and shape. So this is an equilateral triangle. If I take this paper triangle and rotate it 180 degrees., a third of the turn... I'm sorry 120 degrees is a third of a turn, I can match it up with the triangle that I'd drawn. I could rotate it another 120 degrees, another third, and it matches. I could rotate it again, and it will match. Now the smallest number of degrees I needed to rotate that triangle around until it matched was 120 degrees, so we say that this equilateral triangle has 120-degree rotational symmetry. If I have a square, as I have here, I would just have to rotate it 90 degrees until matches up again or a one quarter turn. So that has 90-degree rotational symmetry. So anytime you can take image, rotate it less than a full turn, and have it match up with itself, that's going to be an example of rotational symmetry. I said less than a full turn because if I took this heart that I started out with, I can rotate it 360 degrees and it will match up, because all it's done is gone full-circle. So you have to be able to rotate it less than 360 degrees to have rotational symmetry. Now there's a subset of rotational symmetry that's called point symmetry and point symmetry is a property of anything that has rotational symmetry and can be rotated 180 degrees. So, for instance, this parallelogram... if I start to rotate this I've gotta go all the way through whole half turn, or 180 degrees, before it matches up with itself again. A triangle would not have point symmetry because if I rotated it 180 degrees it's not go to match up with its original. Let me do that again. I'll rotate it 180 degrees and it doesn't match up. A square has point symmetry. I can rotate it less than 180 degrees, I can rotate it 90 degrees, but I CAN rotate it 180 degrees. So as long as I can rotate it 180 degrees and get back to exactly the same image I started with, then I've got point symmetry. So we've got reflection symmetry where we've got a line of symmetry -- you fold an image on itself. And then we've got rotational symmetry where you rotate image around, and within rotational symmetry, if you can rotate it 180 degrees and have it be symmetrical, then it's also called point symmetry. Okay, that's it. Take care. I'll see you next time.
Related tilings
| Uniform heptaheptagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [7,7], (*772) | [7,7]+, (772) | ||||||||||
= |
= |
= |
= |
= |
= |
= |
= | ||||

|

|

|

|

|

|

|

| ||||
| {7,7} | t{7,7} |
r{7,7} | 2t{7,7}=t{7,7} | 2r{7,7}={7,7} | rr{7,7} | tr{7,7} | sr{7,7} | ||||
| Uniform duals | |||||||||||

|

|

|

|

|
|

|
|||||
| V77 | V7.14.14 | V7.7.7.7 | V7.14.14 | V77 | V4.7.4.7 | V4.14.14 | V3.3.7.3.7 | ||||
This tiling is a part of regular series {n,7}:
| Tiles of the form {n,7} | ||||||||
|---|---|---|---|---|---|---|---|---|
| Spherical | Hyperbolic tilings | |||||||
 {2,7} |
 {3,7} |
 {4,7} |
 {5,7} |
 {6,7} |
 {7,7} |
 {8,7} |
... |  {∞,7} |
See also
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch


