| Octahedral prism | |
|---|---|
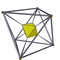
  Schlegel diagram and skew orthogonal projection | |
| Type | Prismatic uniform 4-polytope |
| Uniform index | 51 |
| Schläfli symbol | t{2,3,4} or {3,4}×{} t1,3{3,3,2} or r{3,3}×{} s{2,6}×{} sr{3,2}×{} |
| Coxeter diagram | |
| Cells | 2 (3.3.3.3) 8 (3.4.4) |
| Faces | 16 {3}, 12 {4} |
| Edges | 30 (2×12+6) |
| Vertices | 12 (2×6) |
| Vertex figure |  Square pyramid |
| Dual polytope | Cubic bipyramid |
| Symmetry | [3,4,2], order 96 [3,3,2], order 48 [6,2+,2], order 24 [(3,2)+,2], order 12 |
| Properties | convex, Hanner polytope |
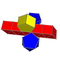
 Net | |
In geometry, an octahedral prism is a convex uniform 4-polytope. This 4-polytope has 10 polyhedral cells: 2 octahedra connected by 8 triangular prisms.
Alternative names
- Octahedral dyadic prism (Norman W. Johnson)
- Ope (Jonathan Bowers, for octahedral prism)
- Triangular antiprismatic prism
- Triangular antiprismatic hyperprism
Coordinates
It is a Hanner polytope with vertex coordinates, permuting first 3 coordinates:
- ([±1,0,0]; ±1)
Structure
The octahedral prism consists of two octahedra connected to each other via 8 triangular prisms. The triangular prisms are joined to each other via their square faces.
Projections

The octahedron-first orthographic projection of the octahedral prism into 3D space has an octahedral envelope. The two octahedral cells project onto the entire volume of this envelope, while the 8 triangular prismic cells project onto its 8 triangular faces.
The triangular-prism-first orthographic projection of the octahedral prism into 3D space has a hexagonal prismic envelope. The two octahedral cells project onto the two hexagonal faces. One triangular prismic cell projects onto a triangular prism at the center of the envelope, surrounded by the images of 3 other triangular prismic cells to cover the entire volume of the envelope. The remaining four triangular prismic cells are projected onto the entire volume of the envelope as well, in the same arrangement, except with opposite orientation.
Related polytopes
It is the second in an infinite series of uniform antiprismatic prisms.
| Name | s{2,2}×{} | s{2,3}×{} | s{2,4}×{} | s{2,5}×{} | s{2,6}×{} | s{2,7}×{} | s{2,8}×{} | s{2,p}×{} |
|---|---|---|---|---|---|---|---|---|
| Coxeter diagram |
||||||||
| Image | 
|
|

|

|
|

|

|

|
| Vertex figure |

|

|
||||||
| Cells | 2 s{2,2} (2) {2}×{}={4} 4 {3}×{} |
2 s{2,3} 2 {3}×{} 6 {3}×{} |
2 s{2,4} 2 {4}×{} 8 {3}×{} |
2 s{2,5} 2 {5}×{} 10 {3}×{} |
2 s{2,6} 2 {6}×{} 12 {3}×{} |
2 s{2,7} 2 {7}×{} 14 {3}×{} |
2 s{2,8} 2 {8}×{} 16 {3}×{} |
2 s{2,p} 2 {p}×{} 2p {3}×{} |
| Net | 
|

|

|
|

|

|

|

|
It is one of 18 uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids and Archimedean solids.
It is one of four four-dimensional Hanner polytopes; the other three are the tesseract, the 16-cell, and the dual of the octahedral prism (a cubical bipyramid).[1]
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
External links
- 6. Convex uniform prismatic polychora - Model 51, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) x x3o4o - ope".
