
In music notation, a note value indicates the relative duration of a note, using the texture or shape of the notehead, the presence or absence of a stem, and the presence or absence of flags/beams/hooks/tails. Unmodified note values are fractional powers of two, for example one, one-half, one fourth, etc.
A rest indicates a silence of an equivalent duration.
YouTube Encyclopedic
-
1/5Views:1 4852 8971 1944343 324
-
Learn to Read Music - What is music note value?
-
#03 Staff Notations Lessons - What is Note Value & Symbols (Hindi)
-
How to read notation ( Lesson 1) | Note value counting
-
CSHT "Grossi," exercise 31 mini lesson on rhythm and note value
-
Note Value Awareness - Taking a Melody and Using Emotion to Add Chords
Transcription
List
| Note | Rest | American name | British name | Relative value | Dotted value | Double dotted value | Triple dotted value |
|---|---|---|---|---|---|---|---|
 |
large, duplex longa, or maxima[1][2] (occasionally octuple note,[3] octuple whole note,[4] or octuple entire musical note)[5] |
8 | 8 + 4 = 12 |
8 + 4 + 2 = 14 |
8 + 4 + 2 + 1 = 15 | ||
| long[2][6][7] or longa[8] (occasionally quadruple note[9] or quadruple whole note)[4] |
4 | 4 + 2 = 6 |
4 + 2 + 1 = 7 |
4 + 2 + 1 + 1/2 = 7+1/2 | |||
| double whole note,[10] double note[11][12][13] | breve | 2 | 2 + 1 = 3 |
2 + 1 + 1/2 = 3+1/2 |
2 + 1 + 1/2 + 1/4 = 3+3/4 | ||
| whole note | semibreve | 1 | 1 + 1/2 = 1+1/2 |
1 + 1/2 + 1/4 = 1+3/4 |
1 + 1/2 + 1/4 + 1/8 = 1+7/8 | ||
| half note | minim | 1/2 | 1/2 + 1/4 = 3/4 |
1/2 + 1/4 + 1/8 = 7/8 |
1/2 + 1/4 + 1/8 + 1/16 = 15/16 | ||
| quarter note | crotchet | 1/4 | 1/4 + 1/8 = 3/8 |
1/4 + 1/8 + 1/16 = 7/16 |
1/4 + 1/8 + 1/16 + 1/32 = 15/32 | ||
 |
eighth note | quaver | 1/8 | 1/8 + 1/16 = 3/16 |
1/8 + 1/16 + 1/32 = 7/32 |
1/8 + 1/16 + 1/32 + 1/64 = 15/64 | |
| sixteenth note | semiquaver | 1/16 | 1/16 + 1/32 = 3/32 |
1/16 + 1/32 + 1/64 = 7/64 |
1/16 + 1/32 + 1/64 + 1/128 = 15/128 | ||
| thirty-second note | demisemiquaver | 1/32 | 1/32 + 1/64 = 3/64 |
1/32 + 1/64 + 1/128 = 7/128 |
1/32 + 1/64 + 1/128 + 1/256 = 15/256 | ||
| sixty-fourth note | hemidemisemiquaver | 1/64 | 1/64 + 1/128 = 3/128 |
1/64 + 1/128 + 1/256 = 7/256 |
1/64 + 1/128 + 1/256 + 1/512 = 15/512 | ||
| hundred twenty-eighth note | semihemidemisemiquaver[14][15] (rare) | 1/128 | 1/128 + 1/256 = 3/256 |
1/128 + 1/256 + 1/512 = 7/512 |
1/128 + 1/256 + 1/512 + 1/1024 = 15/1024 | ||
 |
 |
two hundred fifty-sixth note | demisemihemidemisemiquaver[4] (rare) | 1/256 | 1/256 + 1/512 = 3/512 |
1/256 + 1/512 + 1/1024 = 7/1024 |
1/256 + 1/512 + 1/1024 + 1/2048 = 15/2048 |
Shorter notes can be created theoretically ad infinitum by adding further flags, but are very rare.
Variations

The breve appears in several different versions, as shown at right. The first two are commonly used; the third is a stylistic alternative.
Sometimes the longa or breve is used to indicate a very long note of indefinite duration, as at the end of a piece (e.g. at the end of Mozart's Mass KV 192).
A single eighth note, or any faster note, is always stemmed with flags, while two or more are usually beamed in groups.[16] When a stem is present, it can go either up (from the right side of the note head) or down (from the left side), except in the cases of the longa or maxima which are nearly always written with downward stems. In most cases, the stem goes down if the notehead is on the center line or above, and up otherwise. Any flags always go to the right of the stem.
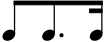
Modifiers
A note value may be augmented by adding a dot after it. This dot adds the next briefer note value, making it one and a half times its original duration. A number of dots (n) lengthen the note value by 2n − 1/2n its value, so two dots add two lower note values, making a total of one and three quarters times its original duration. The rare three dots make it one and seven eighths the duration, and so on.
The double dot was first used in 1752 by J. J. Quantz;[17] in music of the 18th century and earlier the amount by which the dot augmented the note varied: it could be more or less than the modern interpretation, to fit into the context.[17]
To divide a note value to three equal parts, or some other value than two, tuplets may be used. However, see swung note and notes inégales.
History
Gregorian chant
Although note heads of various shapes, and notes with and without stems appear in early Gregorian chant manuscripts, many scholars agree that these symbols do not indicate different durations, although the dot is used for augmentation. See neume.
In the 13th century, chant was sometimes performed according to rhythmic modes, roughly equivalent to meters; however, the note shapes still did not indicate duration in the same way as modern note values.
Mensural notation
Around 1250, Franco of Cologne invented different symbols for different durations, although the relation between different note values could vary; three was the most common ratio. Philippe de Vitry's treatise Ars nova (1320) described a system in which the ratios of different note values could be 2:1 or 3:1, with a system of mensural time signatures to distinguish between them.
This black mensural notation gave way to white mensural notation around 1450, in which all note values were written with white (outline) noteheads. In white notation the use of triplets was indicated by coloration, i.e. filling in the noteheads to make them black (or sometimes red). Both black and white notation periodically made use of ligatures, a holdover from the clivis and porrectus neumes used in chant.
Around 1600 the modern notational system was generally adopted, along with barlines and the practice of writing multipart music in scores rather than only individual parts. In the 17th century, however, old usages came up occasionally.
Origins of the names
The British names go back at least to English renaissance music, and the terms of Latin origin had international currency at that time. Longa means 'long', and many of the rest indicate relative shortness. Breve is from Latin brevis, 'short', minim is from minimus, 'very small', and quaver refers to the quavering effect of very fast notes. The elements semi-, demi- and hemi- mean 'half' in Latin, French and Greek respectively. The chain semantic shift whereby notes which were originally perceived as short came progressively to be long notes is interesting both linguistically and musically. However, the crotchet is named after the shape of the note, from the Old French for a 'little hook', and it is possible to argue that the same is true of the minim, since the word is also used in palaeography to mean a vertical stroke in mediaeval handwriting.
References
- ^ William Smythe, Babcock Mathews, and Emil Liebling, "Large", Pronouncing and Defining Dictionary of Music (Cincinnati, New York, London: J. Church and Company, 1896).
- ^ a b Theodore Baker, A Dictionary of Musical Terms: Containing Upwards of 9,000 English, French, German, Italian, Latin, and Greek Words and Phrases, third edition, revised and enlarged (New York: G. Schirmer, 1897): 131.
- ^ Ray M. Owen "Glossary of Film Terms: Normal v — Noth". SoundsOfNewMexico.com, 2012. Archived 13 August 2016 at the Wayback Machine MC Peko, "bpm calc 2.2 // for calculating and visualizing bpm and related values // help // change-log // open source: zip js". Focus Studios, 2015.
- ^ a b c Kartik Asooja, Sindhu Kiranmai, and Paul Buitelaar "UNLP at the C@merata Task: Question Answering on Musical Scores ACM"
- ^ Anonymous, "My Ambient Sounds—Sleeping Music & Ambient Soundscape Mixer to Help You Sleep Better Now" (10 February 2016) Main Facts.biz (accessed 18 June 2016).
- ^ Music Dictionary (Do–Dq) Dolmetsch.com (accessed 4 February 2015).
- ^ William Smythe, Babcock Mathews, and Emil Liebling, "Double Note", Pronouncing and Defining Dictionary of Music (Cincinnati, New York, London: J. Church and Company, 1896).
- ^ John Morehen and Richard Rastall, "Note values"", The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell (London: Macmillan Publishers, 2001).
- ^ John Freckleton Burrowes, Burrowes' Piano-forte Primer: Containing the Rudiments of Music Adapted for Either Private Tuition Or Teaching in Classes Together with a Guide to Practice, new edition, revised and modernized, with important additions,m by L.H. Southard (Boston and New York: Oliver Ditson, 1874): 41. Hendrik Van der Werf,.. The Oldest Extant Part Music and the Origin of Western Polyphony, 2 vols (Rochester, New York: H. van der Werf, 1993:. 1:97.
- ^ John Morehen and Richard Rastall, "Breve" and "Note values", New Grove Dictionary of Music and Musicians, second edition (2001).
- ^ "Double Note", Webster's Revised Unabridged Dictionary (C. & G. Merriam Co., 1913).
- ^ "Music Dictionary (Do–Dq)" Dolmetsch.com (accessed 4 February 2015).
- ^ Lowell Mason, Manual of the Boston Academy of Music (Boston, 1843): 67.
- ^ Robert J. Miller (2015). Contemporary Orchestration: A Practical Guide to Instruments, Ensembles, and Musicians. London: Routledge. p. 38. ISBN 978-0-415-74190-3.
- ^ David Haas (2011). "Shostakovich's Second Piano Sonata: A Composition Recital in Three Styles". In Pauline Fairclough; David Fanning (eds.). The Cambridge Companion to Shostakovich. Cambridge Companions to Music. Cambridge and New York: Cambridge University Press. pp. 95–114. doi:10.1017/CCOL9780521842204.006. ISBN 978-1-139-00195-3.
The listener is right to suspect a Baroque reference when a double-dotted rhythmic gesture and semihemidemisemiquaver triplets appear to ornament the theme.
(p. 112) - ^ Gerou, Tom (1996). Essential Dictionary of Music Notation, p.211. Alfred. ISBN 0-88284-730-9
- ^ a b Willi Apel, "Dotted Notes", Harvard Dictionary of Music, second edition, revised and enlarged (Cambridge, Massachusetts: Belknap Press of Harvard University Press, 1972) ISBN 978-0-674-37501-7.
