A negative-feedback amplifier (or feedback amplifier) is an electronic amplifier that subtracts a fraction of its output from its input, so that negative feedback opposes the original signal.[1] The applied negative feedback can improve its performance (gain stability, linearity, frequency response, step response) and reduces sensitivity to parameter variations due to manufacturing or environment. Because of these advantages, many amplifiers and control systems use negative feedback.[2]
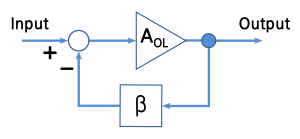
An idealized negative-feedback amplifier as shown in the diagram is a system of three elements (see Figure 1):
- an amplifier with gain AOL,
- a feedback network β, which senses the output signal and possibly transforms it in some way (for example by attenuating or filtering it),
- a summing circuit that acts as a subtractor (the circle in the figure), which combines the input and the transformed output.
YouTube Encyclopedic
-
1/5Views:55 44916 06325 5016 9857 992
-
Mod-04 Lec-16 Feedback in amplifiers, Feedback Configurations and multi stage amplifiers
-
LEARN AND GROW ! FEEDBACK AMPLIFIER !!
-
LEARN AND GROW ! VOLTAGE SERIES AND SHUNT FEEDBACK !!
-
Feedback in Amplifiers | Principle and Advantages | Physics Videos
-
ShuntSeries
Transcription
Overview
Fundamentally, all electronic devices that provide power gain (e.g., vacuum tubes, bipolar transistors, MOS transistors) are nonlinear. Negative feedback trades gain for higher linearity (reducing distortion) and can provide other benefits. If not designed correctly, amplifiers with negative feedback can under some circumstances become unstable due to the feedback becoming positive, resulting in unwanted behavior such as oscillation. The Nyquist stability criterion developed by Harry Nyquist of Bell Laboratories is used to study the stability of feedback amplifiers.
Feedback amplifiers share these properties:[3]
Pros:
- Can increase or decrease input impedance (depending on type of feedback).
- Can increase or decrease output impedance (depending on type of feedback).
- Reduces total distortion if sufficiently applied (increases linearity).
- Increases the bandwidth.
- Desensitizes gain to component variations.
- Can control step response of amplifier.
Cons:
- May lead to instability if not designed carefully.
- Amplifier gain decreases.
- Input and output impedances of a negative-feedback amplifier (closed-loop amplifier) become sensitive to the gain of an amplifier without feedback (open-loop amplifier)—that exposes these impedances to variations in the open-loop gain, for example, due to parameter variations or nonlinearity of the open-loop gain.
- Changes the composition of the distortion (increasing audibility) if insufficiently applied.
History
Paul Voigt patented a negative feedback amplifier in January 1924, though his theory lacked detail.[4] Harold Stephen Black independently invented the negative-feedback amplifier while he was a passenger on the Lackawanna Ferry (from Hoboken Terminal to Manhattan) on his way to work at Bell Laboratories (located in Manhattan instead of New Jersey in 1927) on August 2, 1927[5] (US Patent 2,102,671,[6] issued in 1937). Black was working on reducing distortion in repeater amplifiers used for telephone transmission. On a blank space in his copy of The New York Times,[7] he recorded the diagram found in Figure 1 and the equations derived below.[8] On August 8, 1928, Black submitted his invention to the U. S. Patent Office, which took more than 9 years to issue the patent. Black later wrote: "One reason for the delay was that the concept was so contrary to established beliefs that the Patent Office initially did not believe it would work."[9]
Classical feedback
Using the model of two unilateral blocks, several consequences of feedback are simply derived.
Gain reduction
Below, the voltage gain of the amplifier with feedback, the closed-loop gain AFB, is derived in terms of the gain of the amplifier without feedback, the open-loop gain AOL and the feedback factor β, which governs how much of the output signal is applied to the input (see Figure 1). The open-loop gain AOL in general may be a function of both frequency and voltage; the feedback parameter β is determined by the feedback network that is connected around the amplifier. For an operational amplifier, two resistors forming a voltage divider may be used for the feedback network to set β between 0 and 1. This network may be modified using reactive elements like capacitors or inductors to (a) give frequency-dependent closed-loop gain as in equalization/tone-control circuits or (b) construct oscillators. The gain of the amplifier with feedback is derived below in the case of a voltage amplifier with voltage feedback.
Without feedback, the input voltage V′in is applied directly to the amplifier input. The according output voltage is
Suppose now that an attenuating feedback loop applies a fraction of the output to one of the subtractor inputs so that it subtracts from the circuit input voltage Vin applied to the other subtractor input. The result of subtraction applied to the amplifier input is
Substituting for V′in in the first expression,
Rearranging:
Then the gain of the amplifier with feedback, called the closed-loop gain, AFB is given by
If AOL ≫ 1, then AFB ≈ 1 / β, and the effective amplification (or closed-loop gain) AFB is set by the feedback constant β, and hence set by the feedback network, usually a simple reproducible network, thus making linearizing and stabilizing the amplification characteristics straightforward. If there are conditions where β AOL = −1, the amplifier has infinite amplification – it has become an oscillator, and the system is unstable. The stability characteristics of the gain feedback product β AOL are often displayed and investigated on a Nyquist plot (a polar plot of the gain/phase shift as a parametric function of frequency). A simpler, but less general technique, uses Bode plots.
The combination L = −β AOL appears commonly in feedback analysis and is called the loop gain. The combination (1 + β AOL) also appears commonly and is variously named as the desensitivity factor, return difference, or improvement factor.[10]
Summary of terms
- Open-loop gain = [11][12][13][14]
- Closed-loop gain =
- Feedback factor =
- Noise gain = [dubious ]
- Loop gain =
- Desensitivity factor =
Bandwidth extension

Feedback can be used to extend the bandwidth of an amplifier at the cost of lowering the amplifier gain.[15] Figure 2 shows such a comparison. The figure is understood as follows. Without feedback the so-called open-loop gain in this example has a single-time-constant frequency response given by
where fC is the cutoff or corner frequency of the amplifier: in this example fC = 104 Hz, and the gain at zero frequency A0 = 105 V/V. The figure shows that the gain is flat out to the corner frequency and then drops. When feedback is present, the so-called closed-loop gain, as shown in the formula of the previous section, becomes
The last expression shows that the feedback amplifier still has a single-time-constant behavior, but the corner frequency is now increased by the improvement factor (1 + β A0), and the gain at zero frequency has dropped by exactly the same factor. This behavior is called the gain–bandwidth tradeoff. In Figure 2, (1 + β A0) = 103, so AFB(0) = 105 / 103 = 100 V/V, and fC increases to 104 × 103 = 107 Hz.
Multiple poles
When the close-loop gain has several poles, rather than the single pole of the above example, feedback can result in complex poles (real and imaginary parts). In a two-pole case, the result is peaking in the frequency response of the feedback amplifier near its corner frequency and ringing and overshoot in its step response. In the case of more than two poles, the feedback amplifier can become unstable and oscillate. See the discussion of gain margin and phase margin. For a complete discussion, see Sansen.[16]
Signal-flow analysis
A principal idealization behind the formulation of the Introduction is the network's division into two autonomous blocks (that is, with their own individually determined transfer functions), a simple example of what often is called "circuit partitioning",[17] which refers in this instance to the division into a forward amplification block and a feedback block. In practical amplifiers, the information flow is not unidirectional as shown here.[18] Frequently these blocks are taken to be two-port networks to allow inclusion of bilateral information transfer.[19][20] Casting an amplifier into this form is a non-trivial task, however, especially when the feedback involved is not global (that is directly from the output to the input) but local (that is, feedback within the network, involving nodes that do not coincide with input and/or output terminals).[21][22]
In these more general cases, the amplifier is analyzed more directly without the partitioning into blocks like those in the diagram, using instead some analysis based upon signal-flow analysis, such as the return-ratio method or the asymptotic gain model.[24][25][26] Commenting upon the signal-flow approach, Choma says:[27]
- "In contrast to block diagram and two-port approaches to the feedback network analysis problem, signal flow methods mandate no a priori assumptions as to the unilateral or bilateral properties of the open loop and feedback subcircuits. Moreover, they are not predicated on mutually independent open loop and feedback subcircuit transfer functions, and they do not require that feedback be implemented only globally. Indeed signal flow techniques do not even require explicit identification of the open loop and feedback subcircuits. Signal flow thus removes the detriments pervasive of conventional feedback network analyses but additionally, it proves to be computationally efficient as well."
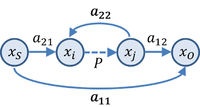
Following up on this suggestion, a signal-flow graph for a negative-feedback amplifier is shown in the figure, which is patterned after one by D'Amico et al..[23] Following these authors, the notation is as follows:
- "Variables xS, xO represent the input and output signals, moreover, two other generic variables, xi, xj linked together through the control (or critical) parameter P are explicitly shown. Parameters aij are the weight branches. Variables xi, xj and the control parameter, P, model a controlled generator, or the relation between voltage and current across two nodes of the circuit.
- The term a11 is the transfer function between the input and the output [after] setting the control parameter, P, to zero; term a12 is the transfer function between the output and the controlled variable xj [after] setting the input source, xS, to zero; term a21 represents the transfer function between the source variable and the inner variable, xi when the controlled variable xj is set to zero (i.e., when the control parameter, P is set to zero); term a22 gives the relation between the independent and the controlled inner variables setting control parameter, P and input variable, xS, to zero."
Using this graph, these authors derive the generalized gain expression in terms of the control parameter P that defines the controlled source relationship xj = Pxi:
Combining these results, the gain is given by
To employ this formula, one has to identify a critical controlled source for the particular amplifier circuit in hand. For example, P could be the control parameter of one of the controlled sources in a two-port network, as shown for a particular case in D'Amico et al.[23] As a different example, if we take a12 = a21 = 1, P = A, a22 = –β (negative feedback) and a11 = 0 (no feedforward), we regain the simple result with two unidirectional blocks.
Two-port analysis of feedback

Although, as mentioned in the section Signal-flow analysis, some form of signal-flow analysis is the most general way to treat the negative-feedback amplifier, representation as two two-ports is the approach most often presented in textbooks and is presented here. It retains a two-block circuit partition of the amplifier, but allows the blocks to be bilateral. Some drawbacks of this method are described at the end.
Electronic amplifiers use current or voltage as input and output, so four types of amplifier are possible (any of two possible inputs with any of two possible outputs). See classification of amplifiers. The objective for the feedback amplifier may be any one of the four types of amplifier and is not necessarily the same type as the open-loop amplifier, which itself may be any one of these types. So, for example, an op amp (voltage amplifier) can be arranged to make a current amplifier instead.
Negative-feedback amplifiers of any type can be implemented using combinations of two-port networks. There are four types of two-port network, and the type of amplifier desired dictates the choice of two-ports and the selection of one of the four different connection topologies shown in the diagram. These connections are usually referred to as series or shunt (parallel) connections.[29][30] In the diagram, the left column shows shunt inputs; the right column shows series inputs. The top row shows series outputs; the bottom row shows shunt outputs. The various combinations of connections and two-ports are listed in the table below.
| Feedback amplifier type | Input connection | Output connection | Ideal feedback | Two-port feedback |
|---|---|---|---|---|
| Current | Shunt | Series | CCCS | g-parameter |
| Transresistance | Shunt | Shunt | CCVS | y-parameter |
| Transconductance | Series | Series | VCCS | z-parameter |
| Voltage | Series | Shunt | VCVS | h-parameter |
For example, for a current-feedback amplifier, current from the output is sampled for feedback and combined with current at the input. Therefore, the feedback ideally is performed using an (output) current-controlled current source (CCCS), and its imperfect realization using a two-port network also must incorporate a CCCS, that is, the appropriate choice for feedback network is a g-parameter two-port. Here the two-port method used in most textbooks is presented,[31][32][33][34] using the circuit treated in the article on asymptotic gain model.

Figure 3 shows a two-transistor amplifier with a feedback resistor Rf. The aim is to analyze this circuit to find three items: the gain, the output impedance looking into the amplifier from the load, and the input impedance looking into the amplifier from the source.
Replacement of the feedback network with a two-port
The first step is replacement of the feedback network by a two-port. Just what components go into the two-port?
On the input side of the two-port we have Rf. If the voltage at the right side of Rf changes, it changes the current in Rf that is subtracted from the current entering the base of the input transistor. That is, the input side of the two-port is a dependent current source controlled by the voltage at the top of resistor R2.
One might say the second stage of the amplifier is just a voltage follower, transmitting the voltage at the collector of the input transistor to the top of R2. That is, the monitored output signal is really the voltage at the collector of the input transistor. That view is legitimate, but then the voltage follower stage becomes part of the feedback network. That makes analysis of feedback more complicated.

An alternative view is that the voltage at the top of R2 is set by the emitter current of the output transistor. That view leads to an entirely passive feedback network made up of R2 and Rf. The variable controlling the feedback is the emitter current, so the feedback is a current-controlled current source (CCCS). We search through the four available two-port networks and find the only one with a CCCS is the g-parameter two-port, shown in Figure 4. The next task is to select the g-parameters so that the two-port of Figure 4 is electrically equivalent to the L-section made up of R2 and Rf. That selection is an algebraic procedure made most simply by looking at two individual cases: the case with V1 = 0, which makes the VCVS on the right side of the two-port a short-circuit; and the case with I2 = 0. which makes the CCCS on the left side an open circuit. The algebra in these two cases is simple, much easier than solving for all variables at once. The choice of g-parameters that make the two-port and the L-section behave the same way are shown in the table below.
| g11 | g12 | g21 | g22 |
|---|---|---|---|
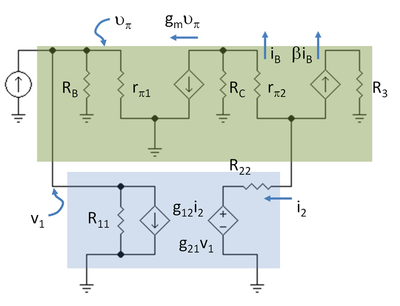
Small-signal circuit
The next step is to draw the small-signal schematic for the amplifier with the two-port in place using the hybrid-pi model for the transistors. Figure 5 shows the schematic with notation R3 = RC2 || RL and R11 = 1 / g11, R22 = g22.
Loaded open-loop gain
Figure 3 indicates the output node, but not the choice of output variable. A useful choice is the short-circuit current output of the amplifier (leading to the short-circuit current gain). Because this variable leads simply to any of the other choices (for example, load voltage or load current), the short-circuit current gain is found below.
First the loaded open-loop gain is found. The feedback is turned off by setting g12 = g21 = 0. The idea is to find how much the amplifier gain is changed because of the resistors in the feedback network by themselves, with the feedback turned off. This calculation is pretty easy because R11, RB, and rπ1 all are in parallel and v1 = vπ. Let R1 = R11 || RB || rπ1. In addition, i2 = −(β+1) iB. The result for the open-loop current gain AOL is:
Gain with feedback
In the classical approach to feedback, the feedforward represented by the VCVS (that is, g21 v1) is neglected.[35] That makes the circuit of Figure 5 resemble the block diagram of Figure 1, and the gain with feedback is then:
where the feedback factor βFB = −g12. Notation βFB is introduced for the feedback factor to distinguish it from the transistor β.
Input and output resistances

Feedback is used to better match signal sources to their loads. For example, a direct connection of a voltage source to a resistive load may result in signal loss due to voltage division, but interjecting a negative feedback amplifier can increase the apparent load seen by the source, and reduce the apparent driver impedance seen by the load, avoiding signal attenuation by voltage division. This advantage is not restricted to voltage amplifiers, but analogous improvements in matching can be arranged for current amplifiers, transconductance amplifiers and transresistance amplifiers.
To explain these effects of feedback upon impedances, first a digression on how two-port theory approaches resistance determination, and then its application to the amplifier at hand.
Background on resistance determination
Figure 6 shows an equivalent circuit for finding the input resistance of a feedback voltage amplifier (left) and for a feedback current amplifier (right). These arrangements are typical Miller theorem applications.
In the case of the voltage amplifier, the output voltage βVout of the feedback network is applied in series and with an opposite polarity to the input voltage Vx travelling over the loop (but in respect to ground, the polarities are the same). As a result, the effective voltage across and the current through the amplifier input resistance Rin decrease so that the circuit input resistance increases (one might say that Rin apparently increases). Its new value can be calculated by applying Miller theorem (for voltages) or the basic circuit laws. Thus Kirchhoff's voltage law provides:
where vout = Av vin = Av Ix Rin. Substituting this result in the above equation and solving for the input resistance of the feedback amplifier, the result is:
The general conclusion from this example and a similar example for the output resistance case is: A series feedback connection at the input (output) increases the input (output) resistance by a factor ( 1 + β AOL ), where AOL = open loop gain.
On the other hand, for the current amplifier, the output current βIout of the feedback network is applied in parallel and with an opposite direction to the input current Ix. As a result, the total current flowing through the circuit input (not only through the input resistance Rin) increases and the voltage across it decreases so that the circuit input resistance decreases (Rin apparently decreases). Its new value can be calculated by applying the dual Miller theorem (for currents) or the basic Kirchhoff's laws:
where iout = Ai iin = Ai Vx / Rin. Substituting this result in the above equation and solving for the input resistance of the feedback amplifier, the result is:
The general conclusion from this example and a similar example for the output resistance case is: A parallel feedback connection at the input (output) decreases the input (output) resistance by a factor ( 1 + β AOL ), where AOL = open loop gain.
These conclusions can be generalized to treat cases with arbitrary Norton or Thévenin drives, arbitrary loads, and general two-port feedback networks. However, the results do depend upon the main amplifier having a representation as a two-port – that is, the results depend on the same current entering and leaving the input terminals, and likewise, the same current that leaves one output terminal must enter the other output terminal.
A broader conclusion, independent of the quantitative details, is that feedback can be used to increase or to decrease the input and output impedance.
Application to the example amplifier
These resistance results now are applied to the amplifier of Figure 3 and Figure 5. The improvement factor that reduces the gain, namely ( 1 + βFB AOL), directly decides the effect of feedback upon the input and output resistances of the amplifier. In the case of a shunt connection, the input impedance is reduced by this factor; and in the case of series connection, the impedance is multiplied by this factor. However, the impedance that is modified by feedback is the impedance of the amplifier in Figure 5 with the feedback turned off, and does include the modifications to impedance caused by the resistors of the feedback network.
Therefore, the input impedance seen by the source with feedback turned off is Rin = R1 = R11 || RB || rπ1, and with the feedback turned on (but no feedforward)
where division is used because the input connection is shunt: the feedback two-port is in parallel with the signal source at the input side of the amplifier. A reminder: AOL is the loaded open loop gain found above, as modified by the resistors of the feedback network.
The impedance seen by the load needs further discussion. The load in Figure 5 is connected to the collector of the output transistor, and therefore is separated from the body of the amplifier by the infinite impedance of the output current source. Therefore, feedback has no effect on the output impedance, which remains simply RC2 as seen by the load resistor RL in Figure 3.[36][37]
If instead we wanted to find the impedance presented at the emitter of the output transistor (instead of its collector), which is series connected to the feedback network, feedback would increase this resistance by the improvement factor ( 1 + βFB AOL).[38]
Load voltage and load current
The gain derived above is the current gain at the collector of the output transistor. To relate this gain to the gain when voltage is the output of the amplifier, notice that the output voltage at the load RL is related to the collector current by Ohm's law as vL = iC (RC2 || RL). Consequently, the transresistance gain vL / iS is found by multiplying the current gain by RC2 || RL:
Similarly, if the output of the amplifier is taken to be the current in the load resistor RL, current division determines the load current, and the gain is then:
Is the main amplifier block a two-port?

Some drawbacks of the two two-port approach follow, intended for the attentive reader.
Figure 7 shows the small-signal schematic with the main amplifier and the feedback two-port in shaded boxes. The feedback two-port satisfies the port conditions: at the input port, Iin enters and leaves the port, and likewise at the output, Iout enters and leaves.
Is the main amplifier block also a two-port? The main amplifier is shown in the upper shaded box. The ground connections are labeled. Figure 7 shows the interesting fact that the main amplifier does not satisfy the port conditions at its input and output unless the ground connections are chosen to make that happen. For example, on the input side, the current entering the main amplifier is IS. This current is divided three ways: to the feedback network, to the bias resistor RB and to the base resistance of the input transistor rπ. To satisfy the port condition for the main amplifier, all three components must be returned to the input side of the main amplifier, which means all the ground leads labeled G1 must be connected, as well as emitter lead GE1. Likewise, on the output side, all ground connections G2 must be connected and also ground connection GE2. Then, at the bottom of the schematic, underneath the feedback two-port and outside the amplifier blocks, G1 is connected to G2. That forces the ground currents to divide between the input and output sides as planned. Notice that this connection arrangement splits the emitter of the input transistor into a base-side and a collector-side – a physically impossible thing to do, but electrically the circuit sees all the ground connections as one node, so this fiction is permitted.
Of course, the way the ground leads are connected makes no difference to the amplifier (they are all one node), but it makes a difference to the port conditions. This artificiality is a weakness of this approach: the port conditions are needed to justify the method, but the circuit really is unaffected by how currents are traded among ground connections.
However, if no possible arrangement of ground conditions leads to the port conditions, the circuit might not behave the same way.[39] The improvement factors (1 + βFB AOL) for determining input and output impedance might not work.[40] This situation is awkward, because a failure to make a two-port may reflect a real problem (it just is not possible), or reflect a lack of imagination (for example, just did not think of splitting the emitter node in two). As a consequence, when the port conditions are in doubt, at least two approaches are possible to establish whether improvement factors are accurate: either simulate an example using Spice and compare results with use of an improvement factor, or calculate the impedance using a test source and compare results.
A more practical choice is to drop the two-port approach altogether, and use various alternatives based on signal flow graph theory, including the Rosenstark method, the Choma method, and use of Blackman's theorem.[41] That choice may be advisable if small-signal device models are complex, or are not available (for example, the devices are known only numerically, perhaps from measurement or from SPICE simulations).
Feedback amplifier formulas
Summarizing the two-port analysis of feedback, one can get this table of formulas.[34]
| Feedback Amplifier | Source Signal | Output Signal | Transfer Function | Input Resistance | Output Resistance |
|---|---|---|---|---|---|
| Series-Shunt (voltage amplifier) | Voltage | Voltage | |||
| Shunt-Series (current amplifier) | Current | Current | |||
| Series-Series(transconductance amplifier) | Voltage | Current | |||
| Shunt-Shunt (transresistance amplifier) | Current | Voltage |
The variables and their meanings are
- gain, - current, - voltage,- feedback gain and - resistance.
The subscripts and their meanings are
- feedback amplifier, - voltage,- transconductance, - transresistance, - output and - current for gains and feedback and - input for resistances.
For example means voltage feedback amplifier gain.[34]
Distortion
Simple amplifiers like the common emitter configuration have primarily low-order distortion, such as the 2nd and 3rd harmonics. In audio systems, these can be minimally audible because musical signals are typically already a harmonic series, and the low-order distortion products are hidden by the masking effect of the human hearing system.[42][43]
After applying moderate amounts of negative feedback (10–15 dB), the low-order harmonics are reduced, but higher-order harmonics are introduced.[44] Since these are not masked as well, the distortion becomes audibly worse, even though the overall THD may go down.[44] This has led to a persistent myth that negative feedback is detrimental in audio amplifiers,[45] leading audiophile manufacturers to market their amplifiers as "zero feedback" (even when they use local feedback to linearize each stage).[46][47]
However, as the amount of negative feedback is increased further, all harmonics are reduced, returning the distortion to inaudibility, and then improving it beyond the original zero-feedback stage (provided the system is strictly stable).[48][45][49] So the problem is not negative feedback, but insufficient amounts of it.
See also
- Asymptotic gain model
- Blackman's theorem
- Bode plot
- Buffer amplifier considers the basic op-amp amplifying stage with negative feedback
- Common collector (emitter follower) is dedicated to the basic transistor amplifying stage with negative feedback
- Extra element theorem
- Frequency compensation
- Miller theorem is a powerful tool for determining the input/output impedances of negative feedback circuits
- Operational amplifier presents the basic op-amp non-inverting amplifier and inverting amplifier
- Operational amplifier applications shows the most typical op-amp circuits with negative feedback
- Phase margin
- Pole splitting
- Return ratio
- Step response
References and notes
- ^ Santiram Kal (2004). Basic Electronics: Devices, Circuits, and IT fundamentals (Paperback ed.). Prentice-Hall of India Pvt Ltd. pp. 191 ff. ISBN 978-8120319523.
- ^ Kuo, Benjamin C. & Farid Golnaraghi (2003). Automatic control systems (Eighth ed.). NY: Wiley. p. 46. ISBN 0-471-13476-7.
- ^ Palumbo, Gaetano & Salvatore Pennisi (2002). Feedback amplifiers: theory and design. Boston/Dordrecht/London: Kluwer Academic. p. 64. ISBN 0-7923-7643-9.
- ^ Jung, Walt (2005). Op Amp Applications Handbook. Newnes. ISBN 9780750678445.
- ^ Black, H. S. (January 1934). "Stabilized Feedback Amplifiers" (PDF). Bell System Tech. J. American Telephone & Telegraph. 13 (1): 1–18. doi:10.1002/j.1538-7305.1934.tb00652.x. Retrieved January 2, 2013.
- ^ Black, Harold (1937-12-21). "U.S. Patent 2,102,671: Wave Translation System" (PDF). www.eepatents.com. Archived from the original (PDF) on 2014-10-06.
- ^ Currently on display at Bell Laboratories in Mountainside, New Jersey.
- ^ Waldhauer, Fred (1982). Feedback. NY: Wiley. p. 3. ISBN 0-471-05319-8.
- ^ Black, Harold (December 1977). "Inventing the negative feedback amplifier". IEEE Spectrum.
- ^ Malik, Norbert R. (January 1995). Electronic Circuits: Analysis, Simulation, and Design. Prentice Hall. ISBN 9780023749100.
- ^ Lu, L. H. "The General Feedback Structure" (PDF). Archived from the original (PDF) on 2016-06-05.
- ^ Self, Douglas (2013-06-18). Audio Power Amplifier Design (6 ed.). New York: Focal Press. p. 54. ISBN 9780240526133.
- ^ Horowitz, Paul; Hill, Winfield (1989-07-28). The Art of Electronics (2 ed.). Cambridge University Press. p. 23. ISBN 9780521370950.
- ^ "MT-044 Op Amp Open Loop Gain and Open Loop Gain Nonlinearity" (PDF). Analog Devices.
β is the feedback loop attenuation, or feedback factor ... noise gain is equal to 1/β
- ^ R. W. Brodersen. Analog circuit design: lectures on stability.
- ^ Willy M. C. Sansen (2006). Analog design essentials. New York; Berlin: Springer. pp. §0513-§0533, p. 155–165. ISBN 0-387-25746-2.
- ^
Partha Pratim Sahu (2013). "§8.2 Partitioning". VLSI Design. McGraw Hill Education. p. 253. ISBN 9781259029844.
dividing a circuit into smaller parts ...[so]...the number of connections between parts is minimized
- ^
Gaetano Palumbo; Salvatore Pennisi (2002). Feedback Amplifiers: Theory and Design. Springer Science & Business Media. ISBN 9780792376439.
In real cases, unfortunately, blocks...cannot be assumed to be unidirectional.
- ^ Wai-Kai Chen (2009). "§1.2 Methods of analysis". Feedback, Nonlinear, and Distributed Circuits. CRC Press. pp. 1–3. ISBN 9781420058826.
- ^ Donald O. Pederson; Kartikeya Mayaram (2007). "§5.2 Feedback for a general amplifier". Analog Integrated Circuits for Communication: Principles, Simulation and Design. Springer Science & Business Media. pp. 105 ff. ISBN 9780387680309.
- ^ Scott K. Burgess & John Choma, Jr. "§6.3 Circuit partitioning" (PDF). Generalized feedback circuit analysis. Archived from the original (PDF) on 2014-12-30.
- ^ Gaetano Palumbo & Salvatore Pennisi (2002). Feedback amplifiers: theory and design. Springer Science & Business Media. p. 66. ISBN 9780792376439.
- ^ a b c
Arnaldo D’Amico, Christian Falconi, Gianluca Giustolisi, Gaetano Palumbo (April 2007). "Resistance of Feedback Amplifiers: A novel representation" (PDF). IEEE Transactions on Circuits and Systems – II Express Briefs. 54 (4): 298–302. CiteSeerX 10.1.1.694.8450. doi:10.1109/TCSII.2006.889713. S2CID 10154732.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ For an introduction, see Rahul Sarpeshkar (2010). "Chapter 10: Return ratio analysis". Ultra Low Power Bioelectronics: Fundamentals, Biomedical Applications, and Bio-Inspired Systems. Cambridge University Press. pp. 240 ff. ISBN 9781139485234.
- ^ Wai-Kai Chen (2005). "§11.2 Methods of analysis". Circuit Analysis and Feedback Amplifier Theory. CRC Press. pp. 11–2 ff. ISBN 9781420037272.
- ^ Gaetano Palumbo; Salvatore Pennisi (2002). "§3.3 The Rosenstark Method and §3.4 The Choma Method". Feedback Amplifiers: Theory and Design. Springer Science & Business Media. pp. 69 ff. ISBN 9780792376439.
- ^ J. Choma, Jr (April 1990). "Signal flow analysis of feedback networks". IEEE Transactions on Circuits and Systems. 37 (4): 455–463. Bibcode:1990ITCS...37..455C. doi:10.1109/31.52748.
- ^
Richard C Jaeger (1997). "Figure 18.2". Microelectronic circuit design (International ed.). McGraw-Hill. p. 986. ISBN 9780070329225.
editions:BZ69IvJlfW8C.
- ^ Ashok K. Goel. Feedback topologies Archived 2008-02-29 at the Wayback Machine.
- ^ Zimmer T., Geoffroy D. Feedback amplifier.
- ^ Vivek Subramanian. Lectures on feedback Archived 2008-02-29 at the Wayback Machine.
- ^ P. R. Gray; P. J. Hurst; S. H. Lewis; R. G. Meyer (2001). Analysis and Design of Analog Integrated Circuits (Fourth ed.). New York: Wiley. pp. 586–587. ISBN 0-471-32168-0.
- ^ A. S. Sedra; K. C. Smith (2004). Microelectronic Circuits (Fifth ed.). New York: Oxford. Example 8.4, pp. 825–829 and PSpice simulation pp. 855–859. ISBN 0-19-514251-9.
- ^ a b c Neaman, Donald. Neamen Electronic Circuit Analysis And Design (4th ed.). pp. 851–946. Chapter 12.
- ^ If the feedforward is included, its effect is to cause a modification of the open-loop gain, normally so small compared to the open-loop gain itself that it can be dropped. Notice also that the main amplifier block is unilateral.
- ^ The use of the improvement factor ( 1 + βFB AOL) requires care, particularly for the case of output impedance using series feedback. See Jaeger, note below.
- ^ R.C. Jaeger & T.N. Blalock (2006). Microelectronic Circuit Design (Third ed.). McGraw-Hill Professional. Example 17.3 pp. 1092–1096. ISBN 978-0-07-319163-8.
- ^ That is, the impedance found by turning off the signal source IS = 0, inserting a test current in the emitter lead Ix, finding the voltage across the test source Vx, and finding Rout = Vx / Ix.
- ^ The equivalence of the main amplifier block to a two-port network guarantees that performance factors work, but without that equivalence they may work anyway. For example, in some cases the circuit can be shown equivalent to another circuit that is a two port, by "cooking up" different circuit parameters that are functions of the original ones. There is no end to creativity!
- ^ Richard C Jaeger; Travis N Blalock (2004). "§18.7: Common errors in applying two-port feedback theory". Microelectronic circuit design (2nd ed.). McGraw=Hill Higher Education. pp. 1409 ff. ISBN 0072320990.
Great care must be exercised in applying two-port theory to ensure that the amplifier feedback networks can actually be represented as two-ports
- ^ Gaetano Palumbo; Salvatore Pennisi (2002). Feedback Amplifiers: Theory and Design. Springer Science & Business Media. p. 66. ISBN 9780792376439.
- ^ "Nonlinear Distortion and Perception at Low Frequencies". Audioholics Home Theater, HDTV, Receivers, Speakers, Blu-ray Reviews and News. 13 August 2015. Retrieved 2016-04-18.
most of the harmonic distortion has been masked, however, a couple of the high order harmonics were far enough away in frequency and loud enough to be heard. So in order to determine the audibility of harmonic distortion, we have to know how much masking is done by different tones at different loudness levels.
- ^ de Santis, Eric Mario; Henin, Simon (2007-06-07). "Perception & Thresholds of Nonlinear Distortion using Complex Signals" (PDF).
Masking is a principle concept in the perception of distortion, as distortion products will only contribute to the percept of distortion if they are not masked by the primary stimulus or other distortion products.
- ^ a b Pass, Nelson (2008-11-01). "Audio distortion and feedback - Passlabs". passlabs.com. Retrieved 2016-04-18.
Here we see that as low feedback figures are applied to a single gain stage the 2nd harmonic declines linearly with feedback, but increased amounts of higher order harmonics are created. As feedback increases above about 15 dB or so, all these forms of distortion [decline] in proportion to increased feedback.
- ^ a b Putzeys, Bruno. "Negative feedback in audio amplifiers: Why there is no such thing as too much (Part 2)". EDN. Retrieved 2016-04-18.
Of course this experiment gives the impression that more feedback is worse. You have to get past that bump. Hardly anybody who has ever tried it like this has actually heard the inevitable (and frankly magical) improvement that happens once you do get beyond, say 20 or 30dB. From there on you get an unambiguous net improvement that goes on forever.
- ^ "Theta Digital – Dreadnaught III Amplifier". www.thetadigital.com. Archived from the original on 2015-11-21. Retrieved 2016-04-18.
Dreadnaught III uses no global negative feedback.
- ^ Martin Colloms (January 1998). "A Future Without Feedback?" (PDF). Stereophile. Archived from the original (PDF) on 2013-06-19. Retrieved 9 May 2007.
- ^ P. J. Baxandall, “Audio power amplifier design”, Wireless World, 1978.
- ^ Bruno Putzeys (February 2011). "The 'F' word, or why there is no such thing as too much feedback" (PDF). Linear Audio. Retrieved 19 March 2013.























































