

In crystallography, the monoclinic crystal system is one of the seven crystal systems. A crystal system is described by three vectors. In the monoclinic system, the crystal is described by vectors of unequal lengths, as in the orthorhombic system. They form a parallelogram prism. Hence two pairs of vectors are perpendicular (meet at right angles), while the third pair makes an angle other than 90°.
YouTube Encyclopedic
-
1/3Views:1 0671 09512 287
-
Monoclinic system فصيلة أحادي الميل
-
Monoclinic crystal structure cell class 12 chemistry solid state
-
Calculus 3: Tensors (7 of 45) Tensors for Crystal Structures: Monoclinic
Transcription
Bravais lattices
Two monoclinic Bravais lattices exist: the primitive monoclinic and the base-centered monoclinic.
| Bravais lattice | Primitive monoclinic |
Base-centered monoclinic |
|---|---|---|
| Pearson symbol | mP | mS |
| Unit cell | 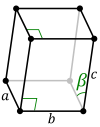
|

|
For the base-centered monoclinic lattice, the primitive cell has the shape of an oblique rhombic prism;[1] it can be constructed because the two-dimensional centered rectangular base layer can also be described with primitive rhombic axes. The length of the primitive cell below equals of the conventional cell above.
Crystal classes
The table below organizes the space groups of the monoclinic crystal system by crystal class. It lists the International Tables for Crystallography space group numbers,[2] followed by the crystal class name, its point group in Schoenflies notation, Hermann–Mauguin (international) notation, orbifold notation, and Coxeter notation, type descriptors, mineral examples, and the notation for the space groups.
| # | Point group | Type | Example | Space groups | |||||
|---|---|---|---|---|---|---|---|---|---|
| Name[3] | Schön. | Intl | Orb. | Cox. | Primitive | Base-centered | |||
| 3–5 | Sphenoidal | C2 | 2 | 22 | [2]+ | enantiomorphic polar | halotrichite | P2, P21 | C2 |
| 6–9 | Domatic | Cs (C1h) | m | *11 | [ ] | polar | hilgardite | Pm, Pc | Cm, Cc |
| 10–12 | Prismatic | C2h | 2/m | 2* | [2,2+] | centrosymmetric | gypsum | P2/m, P21/m | C2/m |
| 13–15 | P2/c, P21/c | C2/c | |||||||
Sphenoidal is also called monoclinic hemimorphic, domatic is also called monoclinic hemihedral, and prismatic is also called monoclinic normal.
The three monoclinic hemimorphic space groups are as follows:
- a prism with a wallpaper group p2 cross-section
- ditto with screw axes instead of axes
- ditto with screw axes as well as axes, parallel, in between; in this case an additional translation vector is one half of a translation vector in the base plane plus one half of a perpendicular vector between the base planes.
The four monoclinic hemihedral space groups include
- those with pure reflection at the base of the prism and halfway
- those with glide planes instead of pure reflection planes; the glide is one half of a translation vector in the base plane
- those with both in between each other; in this case an additional translation vector is this glide plus one half of a perpendicular vector between the base planes.
In two dimensions
The only monoclinic Bravais lattice in two dimensions is the oblique lattice.
| Bravais lattice | Oblique |
|---|---|
| Pearson symbol | mp |
| Unit cell | 
|
See also
References
- ^ See Hahn (2002), p. 746, row mC, column Primitive, where the cell parameters are given as a1 = a2, α = β
- ^ Prince, E., ed. (2006). International Tables for Crystallography. International Union of Crystallography. doi:10.1107/97809553602060000001. ISBN 978-1-4020-4969-9. S2CID 146060934.
- ^ "The 32 crystal classes". Retrieved 2018-06-19.
Further reading
- Hurlbut, Cornelius S.; Klein, Cornels (1985). Manual of Mineralogy (20th ed.). pp. 69–73. ISBN 0-471-80580-7.
- Hahn, Theo, ed. (2002). International Tables for Crystallography, Volume A: Space Group Symmetry. Vol. A (5th ed.). Berlin, New York: Springer-Verlag. doi:10.1107/97809553602060000100. ISBN 978-0-7923-6590-7.




