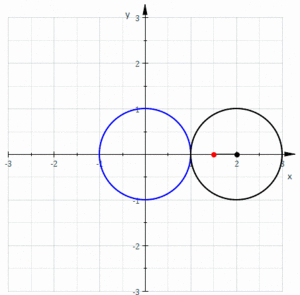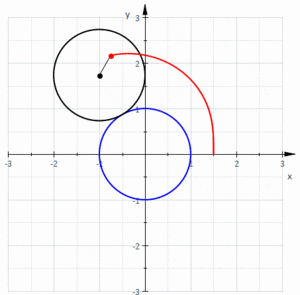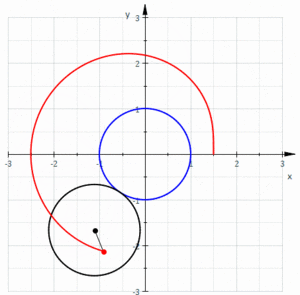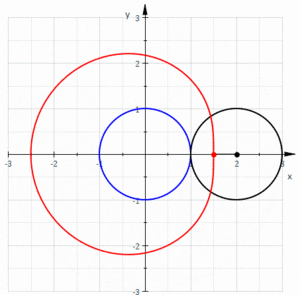
In geometry, a limaçon or limacon /ˈlɪməsɒn/, also known as a limaçon of Pascal or Pascal's Snail, is defined as a roulette curve formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller circle is inside the larger circle. Thus, they belong to the family of curves called centered trochoids; more specifically, they are epitrochoids. The cardioid is the special case in which the point generating the roulette lies on the rolling circle; the resulting curve has a cusp.
Depending on the position of the point generating the curve, it may have inner and outer loops (giving the family its name), it may be heart-shaped, or it may be oval.
A limaçon is a bicircular rational plane algebraic curve of degree 4.

YouTube Encyclopedic
-
1/5Views:22 97574 36680 27714 783784
-
Graphing Limacons
-
Calculus Polar Areas Limacon Example
-
Area of Polar Curve r=1+2cos(theta)
-
Petit escargot et petit limaçon : comptine bébé signe
-
Limacons
Transcription
History
The earliest formal research on limaçons is generally attributed to Étienne Pascal, father of Blaise Pascal. However, some insightful investigations regarding them had been undertaken earlier by the German Renaissance artist Albrecht Dürer. Dürer's Underweysung der Messung (Instruction in Measurement) contains specific geometric methods for producing limaçons. The curve was named by Gilles de Roberval when he used it as an example for finding tangent lines.
Equations
The equation (up to translation and rotation) of a limaçon in polar coordinates has the form
This can be converted to Cartesian coordinates by multiplying by r (thus introducing a point at the origin which in some cases is spurious), and substituting and to obtain[1]
Applying the parametric form of the polar to Cartesian conversion, we also have[2]
while setting
yields this parameterization as a curve in the complex plane:
If we were to shift horizontally by , i.e.,
- ,
we would, by changing the location of the origin, convert to the usual form of the equation of a centered trochoid. Note the change of independent variable at this point to make it clear that we are no longer using the default polar coordinate parameterization .
Special cases
In the special case , the polar equation is
or
making it a member of the sinusoidal spiral family of curves. This curve is the cardioid.
In the special case , the centered trochoid form of the equation becomes
or, in polar coordinates,
making it a member of the rose family of curves. This curve is a trisectrix, and is sometimes called the limaçon trisectrix.
Form
When , the limaçon is a simple closed curve. However, the origin satisfies the Cartesian equation given above, so the graph of this equation has an acnode or isolated point.
When , the area bounded by the curve is convex, and when , the curve has an indentation bounded by two inflection points. At , the point is a point of 0 curvature.
As is decreased relative to , the indentation becomes more pronounced until, at , the curve becomes a cardioid, and the indentation becomes a cusp. For , the cusp expands to an inner loop, and the curve crosses itself at the origin. As approaches 0, the loop fills up the outer curve and, in the limit, the limaçon becomes a circle traversed twice.
Measurement
The area enclosed by the limaçon is . When this counts the area enclosed by the inner loop twice. In this case the curve crosses the origin at angles , the area enclosed by the inner loop is
the area enclosed by the outer loop is
and the area between the loops is
The circumference of the limaçon is given by a complete elliptic integral of the second kind:
Relation to other curves
- Let be a point and be a circle whose center is not . Then the envelope of those circles whose center lies on and that pass through is a limaçon.
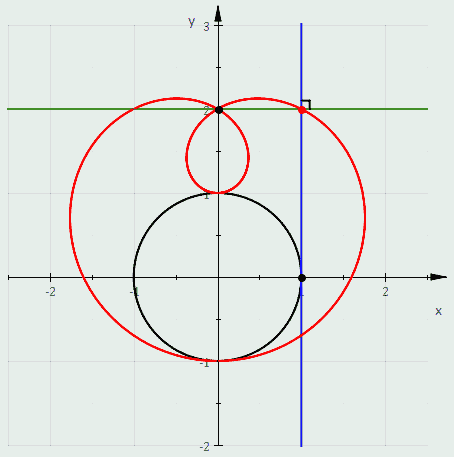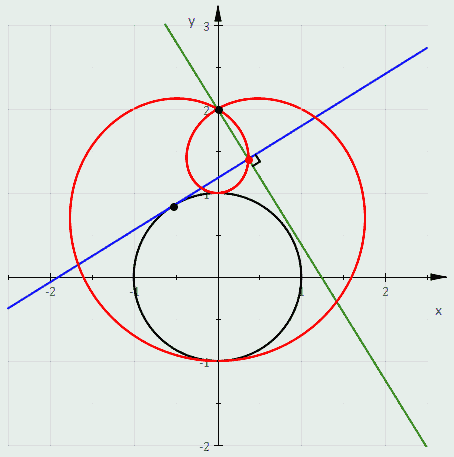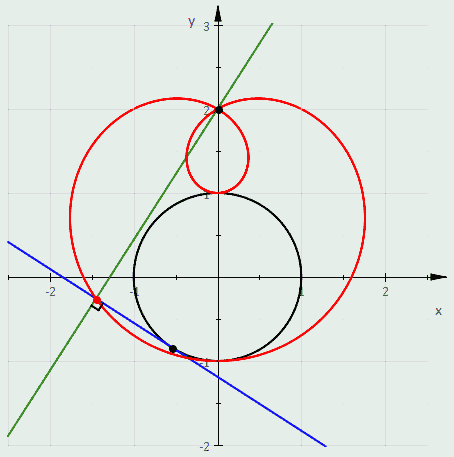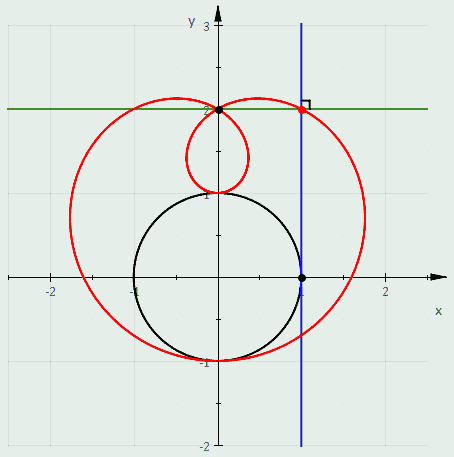
- A pedal of a circle is a limaçon. In fact, the pedal with respect to the origin of the circle with radius and center has polar equation .
- The inverse with respect to the unit circle of is
- which is the equation of a conic section with eccentricity and focus at the origin. Thus a limaçon can be defined as the inverse of a conic where the center of inversion is one of the foci. If the conic is a parabola then the inverse will be a cardioid, if the conic is a hyperbola then the corresponding limaçon will have an inner loop, and if the conic is an ellipse then the corresponding limaçon will have no loop.
- The conchoid of a circle with respect to a point on the circle is a limaçon.
- A particular special case of a Cartesian oval is a limaçon.[3]
See also
References
- ^ a b J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 113–118. ISBN 0-486-60288-5.
- ^ Weisstein, Eric W. "Limaçon." From MathWorld--A Wolfram Web Resource.
- ^ O'Connor, John J.; Robertson, Edmund F., "Cartesian Oval", MacTutor History of Mathematics Archive, University of St Andrews
Further reading
- Jane Grossman and Michael Grossman. "Dimple or no dimple", The Two-Year College Mathematics Journal, January 1982, pages 52–55.
- Howard Anton. Calculus, 2nd edition, page 708, John Wiley & Sons, 1984.
- Howard Anton. [1] pp. 725 – 726.
- Howard Eves. A Survey of Geometry, Volume 2 (pages 51,56,273), Allyn and Bacon, 1965.
External links
- Limacon of Pascal at The MacTutor History of Mathematics
- Limaçon at Mathematical curves
- Limaçon of Pascal at ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES
- Limacon of Pascal at Visual Dictionary of Special Plane Curves
- "Limacon of Pascal" on PlanetPTC (Mathcad)







































