Inscribed angle

In geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. It can also be defined as the angle subtended at a point on the circle by two given points on the circle.

Equivalently, an inscribed angle is defined by two chords of the circle sharing an endpoint.

The inscribed angle theorem relates the measure of an inscribed angle to that of the central angle subtending the same arc.

The inscribed angle theorem appears as Proposition 20 on Book 3 of Euclid's Elements.

YouTube Encyclopedic

1/5
Views:
582 918
976 681
14 249
241 304
381 317

Transcription

What I want to do in this video is to prove one of the more useful results in geometry, and that's that an inscribed angle is just an angle who's vertex sits on the circumference of the circle. So that is our inscribed angle. I'll denote it by si -- I'll use the si for inscribed angle and angles in this video. That si, the inscribed angle, is going to be exactly 1/2 of the central angle that subtends the same arc. So I just used a lot a fancy words, but I think you'll get what I'm saying. So this is si. It is an inscribed angle. It sits, it's vertex sits on the circumference. And if you draw out the to rays that come out from this angle or the two cords that define this angle, it intersects the circle at the other end. And if you look at the part of the circumference of the circle that's inside of it, that is the arc that is subtended by si. It's all very fancy words, but I think the idea is pretty straightforward. This right here is the arc subtended by si, where si is that inscribed angle right over there, the vertex sitting on the circumference. Now, a central angle is an angle where the vertex is sitting at the center of the circle. So let's say that this right here -- I'll try to eyeball it -- that right there is the center of the circle. So let me draw a central angle that subtends this same arc. So that looks like a central angle subtending that same arc. Just like that. Let's call this theta. So this angle is si, this angle right here is theta. When I'm going to prove in this video is that si is always going to be equal to 1/2 of theta. So if I were to tell you that si is equal to, I don't know, 25 degrees, then you would immediately know that theta must be equal to 50 degrees. Or if I told you that theta was 80 degrees, then you would immediately know that si was 40 degrees. So let's actually proved this. So let me clear this. So a good place to start, or the place I'm going to start, is a special case. I'm going to draw a inscribed angle, but one of the cords that define it is going to be the diameter of the circle. So this isn't going to be the general case, this is going to be a special case. So let me see, this is the center right here of my circle. I'm trying to eyeball it. Center looks like that. So let me draw a diameter. So the diameter looks like that. Then let me define my inscribed angle. This diameter is one side of it. And then the other side maybe is just like that. So let me call this right here si. If that's si, this length right here is a radius -- that's our radius of our circle. Then this length right here is also going to be the radius of our circle going from the center to the circumference. Your circumference is defined by all of the points that are exactly a radius away from the center. So that's also a radius. Now, this triangle right here is an isosceles triangle. It has two sides that are equal. Two sides that are definitely equal. We know that when we have two sides being equal, their base angles are also equal. So this will also be equal to si. You might not recognize it because it's tilted up like that. But I think many of us when we see a triangle that looks like this, if I told you this is r and that is r, that these two sides are equal, and if this is si, then you would also know that this angle is also going to be si. Base angles are equivalent on an isosceles triangle. So this is si, that is also si. Now, let me look at the central angle. This is the central angle subtending the same arc. Let's highlight the arc that they're both subtending. This right here is the arc that they're both going to subtend. So this is my central angle right there, theta. Now if this angle is theta, what's this angle going to be? This angle right here. Well, this angle is supplementary to theta, so it's 180 minus theta. When you add these two angles together you go 180 degrees around or the kind of formal line. They're supplementary to each other. Now we also know that these three angles are sitting inside of the same triangle. So they must add up to 180 degrees. So we get si -- this si plus that si plus si plus this angle, which is 180 minus theta plus 180 minus theta. These three angles must add up to 180 degrees. They're the three angles of a triangle. Now we could subtract 180 from both sides. Si plus si is 2 si minus theta is equal to 0. Add theta to both sides. You get 2 si is equal to theta. Multiply both sides by 1/2 or divide both sides by 2. You get si is equal to 1/2 of theta. So we just proved what we set out to prove for the special case where our inscribed angle is defined, where one on the rays, if you want to view these lines as rays, where one of the rays that defines this inscribed angle is along the diameter. The diameter forms part of that ray. So this is a special case where one edge is sitting on the diameter. So already we could generalize this. So now that we know that if this is 50 that this is going to be 100 degrees and likewise, right? Whatever si is or whatever theta is, si's going to be 1/2 of that, or whatever si is, theta is going to be 2 times that. And now this will apply for any time. We could use this notion any time that -- so just using that result we just got, we can now generalize it a little bit, although this won't apply to all inscribed angles. Let's have an inscribed angle that looks like this. So this situation, the center, you can kind of view it as it's inside of the angle. That's my inscribed angle. And I want to find a relationship between this inscribed angle and the central angle that's subtending to same arc. So that's my central angle subtending the same arc. Well, you might say, hey, gee, none of these ends or these cords that define this angle, neither of these are diameters, but what we can do is we can draw a diameter. If the center is within these two cords we can draw a diameter. We can draw a diameter just like that. If we draw a diameter just like that, if we define this angle as si 1, that angle as si 2. Clearly si is the sum of those two angles. And we call this angle theta 1, and this angle theta 2. We immediately you know that, just using the result I just got, since we have one side of our angles in both cases being a diameter now, we know that si 1 is going to be equal to 1/2 theta 1. And we know that si 2 is going to be 1/2 theta 2. Si 2 is going to be 1/2 theta 2. So si, which is si 1 plus si 2, so si 1 plus si 2 is going to be equal to these two things. 1/2 theta 1 plus 1/2 theta 2. Si 1 plus si 2, this is equal to the first inscribed angle that we want to deal with, just regular si. That's si. And this right here, this is equal to 1/2 times theta 1 plus theta 2. What's theta 1 plus theta 2? Well that's just our original theta that we were dealing with. So now we see that si is equal to 1/2 theta. So now we've proved it for a slightly more general case where our center is inside of the two rays that define that angle. Now, we still haven't addressed a slightly harder situation or a more general situation where if this is the center of our circle and I have an inscribed angle where the center isn't sitting inside of the two cords. Let me draw that. So that's going to be my vertex, and I'll switch colors, so let's say that is one of the cords that defines the angle, just like that. And let's say that is the other cord that defines the angle just like that. So how do we find the relationship between, let's call, this angle right here, let's call it si 1. How do we find the relationship between si 1 and the central angle that subtends this same arc? So when I talk about the same arc, that's that right there. So the central angle that subtends the same arc will look like this. Let's call that theta 1. What we can do is use what we just learned when one side of our inscribed angle is a diameter. So let's construct that. So let me draw a diameter here. The result we want still is that this should be 1/2 of this, but let's prove it. Let's draw a diameter just like that. Let me call this angle right here, let me call that si 2. And it is subtending this arc right there -- let me do that in a darker color. It is subtending this arc right there. So the central angle that subtends that same arc, let me call that theta 2. Now, we know from the earlier part of this video that si 2 is going to be equal to 1/2 theta 2, right? They share -- the diameter is right there. The diameter is one of the cords that forms the angle. So si 2 is going to be equal to 1/2 theta 2. This is exactly what we've been doing in the last video, right? This is an inscribed angle. One of the cords that define is sitting on the diameter. So this is going to be 1/2 of this angle, of the central angle that subtends the same arc. Now, let's look at this larger angle. This larger angle right here. Si 1 plus si 2. Right, that larger angle is si 1 plus si 2. Once again, this subtends this entire arc right here, and it has a diameter as one of the cords that defines this huge angle. So this is going to be 1/2 of the central angle that subtends the same arc. We're just using what we've already shown in this video. So this is going to be equal to 1/2 of this huge central angle of theta 1 plus theta 2. So far we've just used everything that we've learned earlier in this video. Now, we already know that si 2 is equal to 1/2 theta 2. So let me make that substitution. This is equal to that. So we can say that si 1 plus -- instead of si 2 I'll write 1/2 theta 2 is equal to 1/2 theta 1 plus 1/2 theta 2. We can subtract 1/2 theta 2 from both sides, and we get our result. Si 1 is equal to 1/2 theta one. And now we're done. We have proven the situation that the inscribed angle is always 1/2 of the central angle that subtends the same arc, regardless of whether the center of the circle is inside of the angle, outside of the angle, whether we have a diameter on one side. So any other angle can be constructed as a sum of any or all of these that we've already done. So hopefully you found this useful and now we can actually build on this result to do some more interesting geometry proofs.

Theorem

Statement

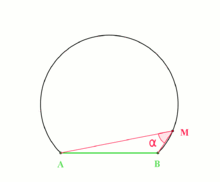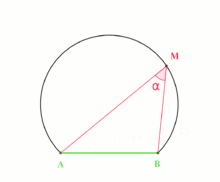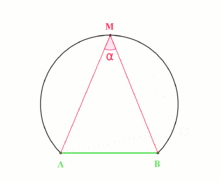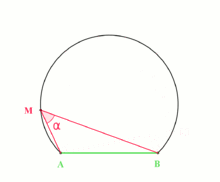
For fixed points $A$ and $B$ , the set of points M in the plane for which the angle $∠ AMB$ is equal to α is an arc of a circle. The measure of $∠ AOB$ , where $O$ is the center of the circle, is $2 α$ .

The inscribed angle theorem states that an angle $θ$ inscribed in a circle is half of the central angle $2 θ$ that subtends the same arc on the circle. Therefore, the angle does not change as its vertex is moved to different positions on the circle.

Proof

Inscribed angles where one chord is a diameter

Let $O$ be the center of a circle, as in the diagram at right. Choose two points on the circle, and call them $V$ and $A$ . Draw line $OV$ and extended past $O$ so that it intersects the circle at point $B$ which is diametrically opposite the point $V$ . Draw an angle whose vertex is point $V$ and whose sides pass through points $A, B$ .

Draw line $OA$ . Angle $∠ BOA$ is a central angle; call it $θ$ . Lines $OV$ and $OA$ are both radii of the circle, so they have equal lengths. Therefore, triangle $△ VOA$ is isosceles, so angle $∠ BVA$ (the inscribed angle) and angle $∠ VAO$ are equal; let each of them be denoted as $ψ$ .

Angles $∠ BOA$ and $∠ AOV$ are supplementary, summing to a straight angle (180°), so angle $∠ AOV$ measures $180° - θ$ .

The three angles of triangle $△ VOA$ must sum to $180°$ :

(180^{\circ }-\theta )+\psi +\psi =180^{\circ }.

Adding $\theta -180^{\circ }$ to both sides yields

2\psi =\theta .

Inscribed angles with the center of the circle in their interior

Case: Center interior to angle
   $φ 0 = ∠ DVC, θ 0 = ∠ DOC$

   $φ 1 = ∠ EVD, θ 1 = ∠ EOD$

   $φ 2 = ∠ EVC, θ 2 = ∠ EOC$

Given a circle whose center is point $O$ , choose three points $V, C, D$ on the circle. Draw lines $VC$ and $VD$ : angle $∠ DVC$ is an inscribed angle. Now draw line $OV$ and extend it past point $O$ so that it intersects the circle at point $E$ . Angle $∠ DVC$ subtends arc $DC$ on the circle.

Suppose this arc includes point $E$ within it. Point $E$ is diametrically opposite to point $V$ . Angles $∠ DVE, ∠ EVC$ are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.

Therefore,

\angle DVC=\angle DVE+\angle EVC.

then let

{\begin{aligned}\psi _{0}&=\angle DVC,\\\psi _{1}&=\angle DVE,\\\psi _{2}&=\angle EVC,\end{aligned}}

so that

\psi _{0}=\psi _{1}+\psi _{2}.\qquad \qquad (1)

Draw lines $OC$ and $OD$ . Angle $∠ DOC$ is a central angle, but so are angles $∠ DOE$ and $∠ EOC$ , and

\angle DOC=\angle DOE+\angle EOC.

Let

{\begin{aligned}\theta _{0}&=\angle DOC,\\\theta _{1}&=\angle DOE,\\\theta _{2}&=\angle EOC,\end{aligned}}

so that

\theta _{0}=\theta _{1}+\theta _{2}.\qquad \qquad (2)

From Part One we know that $\theta _{1}=2\psi _{1}$ and that $\theta _{2}=2\psi _{2}$ . Combining these results with equation (2) yields

\theta _{0}=2\psi _{1}+2\psi _{2}=2(\psi _{1}+\psi _{2})

therefore, by equation (1),

\theta _{0}=2\psi _{0}.

Inscribed angles with the center of the circle in their exterior

The previous case can be extended to cover the case where the measure of the inscribed angle is the difference between two inscribed angles as discussed in the first part of this proof.

Suppose this arc does not include point $E$ within it. Point $E$ is diametrically opposite to point $V$ . Angles $∠ EVD, ∠ EVC$ are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.

Therefore,

\angle DVC=\angle EVC-\angle EVD

then let

{\begin{aligned}\psi _{0}&=\angle DVC,\\\psi _{1}&=\angle EVD,\\\psi _{2}&=\angle EVC,\end{aligned}}

so that

\psi _{0}=\psi _{2}-\psi _{1}.\qquad \qquad (3)

Draw lines $OC$ and $OD$ . Angle $∠ DOC$ is a central angle, but so are angles $∠ EOD$ and $∠ EOC$ , and

\angle DOC=\angle EOC-\angle EOD.

Let

{\begin{aligned}\theta _{0}&=\angle DOC,\\\theta _{1}&=\angle EOD,\\\theta _{2}&=\angle EOC,\end{aligned}}

so that

\theta _{0}=\theta _{2}-\theta _{1}.\qquad \qquad (4)

From Part One we know that $\theta _{1}=2\psi _{1}$ and that $\theta _{2}=2\psi _{2}$ . Combining these results with equation (4) yields

\theta _{0}=2\psi _{2}-2\psi _{1}

therefore, by equation (3),

\theta _{0}=2\psi _{0}.

Corollary

By a similar argument, the angle between a chord and the tangent line at one of its intersection points equals half of the central angle subtended by the chord. See also Tangent lines to circles.

Applications

The inscribed angle theorem is used in many proofs of elementary Euclidean geometry of the plane. A special case of the theorem is Thales' theorem, which states that the angle subtended by a diameter is always 90°, i.e., a right angle. As a consequence of the theorem, opposite angles of cyclic quadrilaterals sum to 180°; conversely, any quadrilateral for which this is true can be inscribed in a circle. As another example, the inscribed angle theorem is the basis for several theorems related to the power of a point with respect to a circle. Further, it allows one to prove that when two chords intersect in a circle, the products of the lengths of their pieces are equal.

Inscribed angle theorems for ellipses, hyperbolas and parabolas

Inscribed angle theorems exist for ellipses, hyperbolas and parabolas, too. The essential differences are the measurements of an angle. (An angle is considered a pair of intersecting lines.)

References

Ogilvy, C. S. (1990). Excursions in Geometry. Dover. pp. 17–23. ISBN 0-486-26530-7.
Gellert W, Küstner H, Hellwich M, Kästner H (1977). The VNR Concise Encyclopedia of Mathematics. New York: Van Nostrand Reinhold. p. 172. ISBN 0-442-22646-2.
Moise, Edwin E. (1974). Elementary Geometry from an Advanced Standpoint (2nd ed.). Reading: Addison-Wesley. pp. 192–197. ISBN 0-201-04793-4.

External links

Weisstein, Eric W. "Inscribed Angle". MathWorld.
Relationship Between Central Angle and Inscribed Angle
Munching on Inscribed Angles at cut-the-knot
Arc Central Angle With interactive animation
Arc Peripheral (inscribed) Angle With interactive animation
Arc Central Angle Theorem With interactive animation
At bookofproofs.github.io

Ancient Greek mathematics

Mathematicians
(timeline)

Treatises

Problems

Concepts
and definitions

Results

In Elements	Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed angle theorem Intercept theorem Intersecting chords theorem Intersecting secants theorem Law of cosines Pons asinorum Pythagorean theorem Tangent-secant theorem Thales's theorem Theorem of the gnomon
Apollonius	Apollonius's theorem
Other	Aristarchus's inequality Crossbar theorem Heron's formula Irrational numbers Law of sines Menelaus's theorem Pappus's area theorem Problem II.8 of Arithmetica Ptolemy's inequality Ptolemy's table of chords Ptolemy's theorem Spiral of Theodorus

Centers

Ancient Greek astronomy Attic numerals Greek numerals Latin translations of the 12th century Non-Euclidean geometry Philosophy of mathematics Neusis construction
History of	A History of Greek Mathematics by Thomas Heath algebra timeline arithmetic timeline calculus timeline geometry timeline logic timeline mathematics timeline numbers prehistoric counting numeral systems list
Other cultures	Arabian/Islamic Babylonian Chinese Egyptian Incan Indian Japanese

Ancient Greece portal •

Mathematics portal

This page was last edited on 9 March 2024, at 00:20

From Wikipedia, the free encyclopedia

YouTube Encyclopedic

Transcription

Theorem

Statement

Proof

Inscribed angles where one chord is a diameter

Inscribed angles with the center of the circle in their interior

Inscribed angles with the center of the circle in their exterior

Corollary

Applications

Inscribed angle theorems for ellipses, hyperbolas and parabolas

References

External links