Heawood conjecture

In graph theory, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary for graph coloring on a surface of a given genus. For surfaces of genus 0, 1, 2, 3, 4, 5, 6, 7, ..., the required number of colors is 4, 7, 8, 9, 10, 11, 12, 12, .... OEIS: A000934, the chromatic number or Heawood number.

The conjecture was formulated in 1890 by P.J. Heawood and proven in 1968 by Gerhard Ringel and J.W.T. Youngs. One case, the non-orientable Klein bottle, proved an exception to the general formula. An entirely different approach was needed for the much older problem of finding the number of colors needed for the plane or sphere, solved in 1976 as the four color theorem by Haken and Appel. On the sphere the lower bound is easy, whereas for higher genera the upper bound is easy and was proved in Heawood's original short paper that contained the conjecture. In other words, Ringel, Youngs, and others had to construct extreme examples for every genus g = 1, 2, 3, …. If g = 12s + k, then the genera fall into the 12 cases as k = 0, 1, 2, 3, …., 11. To simplify, suppose that case k has been established if only a finite number of gs of the form 12s + k are in doubt. Then the years in which the twelve cases were settled, and by whom, are the following:

• 1954, Ringel: case 5
• 1961, Ringel: cases 3, 7, 10
• 1963, Terry, Welch, Youngs: cases 0, 4
• 1964, Gustin, Youngs: case 1
• 1965, Gustin: case 9
• 1966, Youngs: case 6
• 1967, Ringel, Youngs: cases 2, 8, 11

The last seven sporadic exceptions were settled as follows:

• 1967, Mayer: cases 18, 20, 23
• 1968, Ringel, Youngs: cases 30, 35, 47, 59, and the conjecture was proved.

Formal statement

Percy John Heawood conjectured in 1890 that for a given genus g > 0, the minimum number of colors necessary to color all graphs drawn on an orientable surface of that genus (or equivalently, to color the regions of any partition of the surface into simply connected regions) is given by

${\displaystyle \gamma (g)=\left\lfloor {\frac {7+{\sqrt {1+48g}}}{2}}\right\rfloor ,}$

where ${\displaystyle \left\lfloor x\right\rfloor }$ is the floor function.

Replacing the genus by the Euler characteristic, we obtain a formula that covers both the orientable and non-orientable cases,

${\displaystyle \gamma (\chi )=\left\lfloor {\frac {7+{\sqrt {49-24\chi }}}{2}}\right\rfloor .}$

This relation holds, as Ringel and Youngs showed, for all surfaces except for the Klein bottle. Philip Franklin (1930) proved that the Klein bottle requires at most 6 colors, rather than 7 as predicted by the formula. The Franklin graph can be drawn on the Klein bottle in a way that forms six mutually-adjacent regions, showing that this bound is tight.

The upper bound, proved in Heawood's original short paper, is based on a greedy coloring algorithm. By manipulating the Euler characteristic, one can show that every graph embedded in the given surface must have at least one vertex of degree less than the given bound. If one removes this vertex, and colors the rest of the graph, the small number of edges incident to the removed vertex ensures that it can be added back to the graph and colored without increasing the needed number of colors beyond the bound. In the other direction, the proof is more difficult, and involves showing that in each case (except the Klein bottle) a complete graph with a number of vertices equal to the given number of colors can be embedded on the surface.

Example

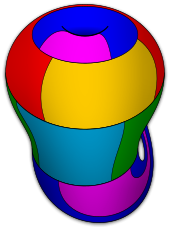
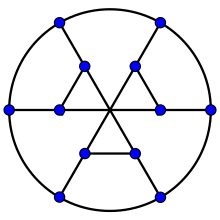
The torus has g = 1, so χ = 0. Therefore, as the formula states, any subdivision of the torus into regions can be colored using at most seven colors. The illustration shows a subdivision of the torus in which each of seven regions are adjacent to each other region; this subdivision shows that the bound of seven on the number of colors is tight for this case. The boundary of this subdivision forms an embedding of the Heawood graph onto the torus.

References

• Franklin, P. (1934). "A six color problem". MIT Journal of Mathematics and Physics. 13 (1–4): 363–379. doi:10.1002/sapm1934131363. hdl:2027/mdp.39015019892200.
• Heawood, P. J. (1890). "Map colour theorem". Quarterly Journal of Mathematics. 24: 332–338.
• Ringel, G.; Youngs, J. W. T. (1968). "Solution of the Heawood map-coloring problem". Proceedings of the National Academy of Sciences of the United States of America. 60 (2): 438–445. Bibcode:1968PNAS...60..438R. doi:10.1073/pnas.60.2.438. MR 0228378. PMC 225066. PMID 16591648.

External links

• Weisstein, Eric W. "Heawood Conjecture". MathWorld.

This page was last edited on 17 March 2024, at 23:47