| Dodecahedral prism | |
|---|---|
 Schlegel diagram Only one dodecahedral cell shown | |
| Type | Prismatic uniform 4-polytope |
| Uniform index | 57 |
| Schläfli symbol | t{2,5,3} or {5,3}×{} |
| Coxeter-Dynkin |     
|
| Cells | 2 (5.5.5) 12 (4.4.5) 
|
| Faces | 30 {4} 24 {5} |
| Edges | 80 |
| Vertices | 40 |
| Vertex figure | 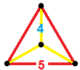 Equilateral-triangular pyramid |
| Dual | Icosahedral bipyramid |
| Symmetry group | [5,3,2], order 240 |
| Properties | convex |
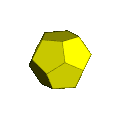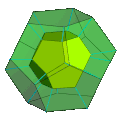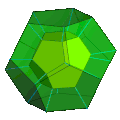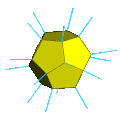
In geometry, a dodecahedral prism is a convex uniform 4-polytope. This 4-polytope has 14 polyhedral cells: 2 dodecahedra connected by 12 pentagonal prisms. It has 54 faces: 30 squares and 24 pentagons. It has 80 edges and 40 vertices.
It can be constructed by creating two coinciding dodecahedra in 3-space, and translating each copy in opposite perpendicular directions in 4-space until their separation equals their edge length.
It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids or Archimedean solids.
Alternative names
- Dodecahedral dyadic prism Norman W. Johnson
- Dodecahedral hyperprism
Images
-
-
Transparent Schlegel diagram -
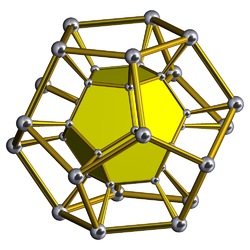
An orthographic projection with a wireframe model and has half of the pentagonal faces colored to show the two dodecahedra. The dodecahedra are regular, but look flattened because of the projection and direction of viewing.
Structure
The dodecahedral prism consists of two dodecahedra connected to each other via 12 pentagonal prisms. The pentagonal prisms are joined to each other via their square faces.
Projections
The pentagonal-prism-first orthographic projection of the dodecahedral prism into 3D space has a decagonal envelope (see diagram). Two of the pentagonal prisms project to the center of this volume, each surrounded by 5 other pentagonal prisms. They form two sets (each consisting of a central pentagonal prism surrounded by 5 other non-uniform pentagonal prisms) that cover the volume of the decagonal prism twice. The two dodecahedra project onto the decagonal faces of the envelope.
The dodecahedron-first orthographic projection of the dodecahedral prism into 3D space has a dodecahedral envelope. The two dodecahedral cells project onto the entire volume of this envelope, while the 12 decagonal prismic cells project onto its 12 pentagonal faces.
External links
- 6. Convex uniform prismatic polychora - Model 57, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) x o3o5x - dope".
This page was last edited on 10 April 2024, at 13:02