Direct limit

In mathematics, a direct limit is a way to construct a (typically large) object from many (typically smaller) objects that are put together in a specific way. These objects may be groups, rings, vector spaces or in general objects from any category. The way they are put together is specified by a system of homomorphisms (group homomorphism, ring homomorphism, or in general morphisms in the category) between those smaller objects. The direct limit of the objects ${\displaystyle A_{i}}$, where ${\displaystyle i}$ ranges over some directed set ${\displaystyle I}$, is denoted by ${\displaystyle \varinjlim A_{i}}$. This notation suppresses the system of homomorphisms; however, the limit depends on the system of homomorphisms.

Direct limits are a special case of the concept of colimit in category theory. Direct limits are dual to inverse limits, which are a special case of limits in category theory.

Formal definition

We will first give the definition for algebraic structures like groups and modules, and then the general definition, which can be used in any category.

Direct limits of algebraic objects

In this section objects are understood to consist of underlying sets equipped with a given algebraic structure, such as groups, rings, modules (over a fixed ring), algebras (over a fixed field), etc. With this in mind, homomorphisms are understood in the corresponding setting (group homomorphisms, etc.).

Let ${\displaystyle \langle I,\leq \rangle }$ be a directed set. Let ${\displaystyle \{A_{i}:i\in I\}}$ be a family of objects indexed by ${\displaystyle I\,}$ and ${\displaystyle f_{ij}\colon A_{i}\rightarrow A_{j}}$ be a homomorphism for all ${\displaystyle i\leq j}$ with the following properties:

1. ${\displaystyle f_{ii}\,}$ is the identity on ${\displaystyle A_{i}\,}$, and
2. ${\displaystyle f_{ik}=f_{jk}\circ f_{ij}}$ for all ${\displaystyle i\leq j\leq k}$.

Then the pair ${\displaystyle \langle A_{i},f_{ij}\rangle }$ is called a direct system over ${\displaystyle I}$.

The direct limit of the direct system ${\displaystyle \langle A_{i},f_{ij}\rangle }$ is denoted by ${\displaystyle \varinjlim A_{i}}$ and is defined as follows. Its underlying set is the disjoint union of the ${\displaystyle A_{i}}$'s modulo a certain equivalence relation ${\displaystyle \sim \,}$:

${\displaystyle \varinjlim A_{i}=\bigsqcup _{i}A_{i}{\bigg /}\sim .}$

Here, if ${\displaystyle x_{i}\in A_{i}}$ and ${\displaystyle x_{j}\in A_{j}}$, then ${\displaystyle x_{i}\sim \,x_{j}}$ if and only if there is some ${\displaystyle k\in I}$ with ${\displaystyle i\leq k}$ and ${\displaystyle j\leq k}$ such that ${\displaystyle f_{ik}(x_{i})=f_{jk}(x_{j})\,}$. Intuitively, two elements in the disjoint union are equivalent if and only if they "eventually become equal" in the direct system. An equivalent formulation that highlights the duality to the inverse limit is that an element is equivalent to all its images under the maps of the direct system, i.e. ${\displaystyle x_{i}\sim \,f_{ij}(x_{i})}$ whenever ${\displaystyle i\leq j}$.

One obtains from this definition canonical functions ${\displaystyle \phi _{j}\colon A_{j}\rightarrow \varinjlim A_{i}}$ sending each element to its equivalence class. The algebraic operations on ${\displaystyle \varinjlim A_{i}\,}$ are defined such that these maps become homomorphisms. Formally, the direct limit of the direct system ${\displaystyle \langle A_{i},f_{ij}\rangle }$ consists of the object ${\displaystyle \varinjlim A_{i}}$ together with the canonical homomorphisms ${\displaystyle \phi _{j}\colon A_{j}\rightarrow \varinjlim A_{i}}$.

Direct limits in an arbitrary category

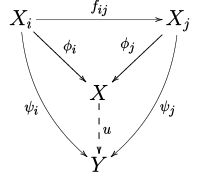
The direct limit can be defined in an arbitrary category ${\displaystyle {\mathcal {C}}}$ by means of a universal property. Let ${\displaystyle \langle X_{i},f_{ij}\rangle }$ be a direct system of objects and morphisms in ${\displaystyle {\mathcal {C}}}$ (as defined above). A target is a pair ${\displaystyle \langle X,\phi _{i}\rangle }$ where ${\displaystyle X\,}$ is an object in ${\displaystyle {\mathcal {C}}}$ and ${\displaystyle \phi _{i}\colon X_{i}\rightarrow X}$ are morphisms for each ${\displaystyle i\in I}$ such that ${\displaystyle \phi _{i}=\phi _{j}\circ f_{ij}}$ whenever ${\displaystyle i\leq j}$. A direct limit of the direct system ${\displaystyle \langle X_{i},f_{ij}\rangle }$ is a universally repelling target ${\displaystyle \langle X,\phi _{i}\rangle }$ in the sense that ${\displaystyle \langle X,\phi _{i}\rangle }$ is a target and for each target ${\displaystyle \langle Y,\psi _{i}\rangle }$, there is a unique morphism ${\displaystyle u\colon X\rightarrow Y}$ such that ${\displaystyle u\circ \phi _{i}=\psi _{i}}$ for each i. The following diagram

will then commute for all i, j.

The direct limit is often denoted

${\displaystyle X=\varinjlim X_{i}}$

with the direct system ${\displaystyle \langle X_{i},f_{ij}\rangle }$ and the canonical morphisms ${\displaystyle \phi _{i}}$ being understood.

Unlike for algebraic objects, not every direct system in an arbitrary category has a direct limit. If it does, however, the direct limit is unique in a strong sense: given another direct limit X′ there exists a unique isomorphism X′ → X that commutes with the canonical morphisms.

Examples

• A collection of subsets ${\displaystyle M_{i}}$ of a set ${\displaystyle M}$ can be partially ordered by inclusion. If the collection is directed, its direct limit is the union ${\displaystyle \bigcup M_{i}}$. The same is true for a directed collection of subgroups of a given group, or a directed collection of subrings of a given ring, etc.
• The weak topology of a CW complex is defined as a direct limit.
• Let ${\displaystyle X}$ be any directed set with a greatest element ${\displaystyle m}$. The direct limit of any corresponding direct system is isomorphic to ${\displaystyle X_{m}}$ and the canonical morphism ${\displaystyle \phi _{m}:X_{m}\rightarrow X}$ is an isomorphism.
• Let K be a field. For a positive integer n, consider the general linear group GL(n;K) consisting of invertible n x n - matrices with entries from K. We have a group homomorphism GL(n;K) → GL(n+1;K) that enlarges matrices by putting a 1 in the lower right corner and zeros elsewhere in the last row and column. The direct limit of this system is the general linear group of K, written as GL(K). An element of GL(K) can be thought of as an infinite invertible matrix that differs from the infinite identity matrix in only finitely many entries. The group GL(K) is of vital importance in algebraic K-theory.
• Let p be a prime number. Consider the direct system composed of the factor groups ${\displaystyle \mathbb {Z} /p^{n}\mathbb {Z} }$ and the homomorphisms ${\displaystyle \mathbb {Z} /p^{n}\mathbb {Z} \rightarrow \mathbb {Z} /p^{n+1}\mathbb {Z} }$ induced by multiplication by ${\displaystyle p}$. The direct limit of this system consists of all the roots of unity of order some power of ${\displaystyle p}$, and is called the Prüfer group ${\displaystyle \mathbb {Z} (p^{\infty })}$.
• There is a (non-obvious) injective ring homomorphism from the ring of symmetric polynomials in ${\displaystyle n}$ variables to the ring of symmetric polynomials in ${\displaystyle n+1}$ variables. Forming the direct limit of this direct system yields the ring of symmetric functions.
• Let F be a C-valued sheaf on a topological space X. Fix a point x in X. The open neighborhoods of x form a directed set ordered by inclusion (U ≤ V if and only if U contains V). The corresponding direct system is (F(U), r_U,V) where r is the restriction map. The direct limit of this system is called the stalk of F at x, denoted F_x. For each neighborhood U of x, the canonical morphism F(U) → F_x associates to a section s of F over U an element s_x of the stalk F_x called the germ of s at x.
• Direct limits in the category of topological spaces are given by placing the final topology on the underlying set-theoretic direct limit.
• An ind-scheme is an inductive limit of schemes.

Properties

Direct limits are linked to inverse limits via

${\displaystyle \mathrm {Hom} (\varinjlim X_{i},Y)=\varprojlim \mathrm {Hom} (X_{i},Y).}$

An important property is that taking direct limits in the category of modules is an exact functor. This means that if you start with a directed system of short exact sequences ${\displaystyle 0\to A_{i}\to B_{i}\to C_{i}\to 0}$ and form direct limits, you obtain a short exact sequence ${\displaystyle 0\to \varinjlim A_{i}\to \varinjlim B_{i}\to \varinjlim C_{i}\to 0}$.

Related constructions and generalizations

We note that a direct system in a category ${\displaystyle {\mathcal {C}}}$ admits an alternative description in terms of functors. Any directed set ${\displaystyle \langle I,\leq \rangle }$ can be considered as a small category ${\displaystyle {\mathcal {I}}}$ whose objects are the elements ${\displaystyle I}$ and there is a morphisms ${\displaystyle i\rightarrow j}$ if and only if ${\displaystyle i\leq j}$. A direct system over ${\displaystyle I}$ is then the same as a covariant functor ${\displaystyle {\mathcal {I}}\rightarrow {\mathcal {C}}}$. The colimit of this functor is the same as the direct limit of the original direct system.

A notion closely related to direct limits are the filtered colimits. Here we start with a covariant functor ${\displaystyle {\mathcal {J}}\to {\mathcal {C}}}$ from a filtered category ${\displaystyle {\mathcal {J}}}$ to some category ${\displaystyle {\mathcal {C}}}$ and form the colimit of this functor. One can show that a category has all directed limits if and only if it has all filtered colimits, and a functor defined on such a category commutes with all direct limits if and only if it commutes with all filtered colimits.^[1]

Given an arbitrary category ${\displaystyle {\mathcal {C}}}$, there may be direct systems in ${\displaystyle {\mathcal {C}}}$ that don't have a direct limit in ${\displaystyle {\mathcal {C}}}$ (consider for example the category of finite sets, or the category of finitely generated abelian groups). In this case, we can always embed ${\displaystyle {\mathcal {C}}}$ into a category ${\displaystyle {\text{Ind}}({\mathcal {C}})}$ in which all direct limits exist; the objects of ${\displaystyle {\text{Ind}}({\mathcal {C}})}$ are called ind-objects of ${\displaystyle {\mathcal {C}}}$.

The categorical dual of the direct limit is called the inverse limit. As above, inverse limits can be viewed as limits of certain functors and are closely related to limits over cofiltered categories.

Terminology

In the literature, one finds the terms "directed limit", "direct inductive limit", "directed colimit", "direct colimit" and "inductive limit" for the concept of direct limit defined above. The term "inductive limit" is ambiguous however, as some authors use it for the general concept of colimit.

See also

• Direct limits of groups

Notes

References

• Bourbaki, Nicolas (1968), Elements of mathematics. Theory of sets, Translated from French, Paris: Hermann, MR 0237342
• Mac Lane, Saunders (1998), Categories for the Working Mathematician, Graduate Texts in Mathematics, vol. 5 (2nd ed.), Springer-Verlag

This page was last edited on 16 March 2024, at 14:50