In computer science, a circular buffer, circular queue, cyclic buffer or ring buffer is a data structure that uses a single, fixed-size buffer as if it were connected end-to-end. This structure lends itself easily to buffering data streams.[1] There were early circular buffer implementations in hardware.[2][3]
YouTube Encyclopedic
-
1/5Views:59 0223971 6937 3778 422
-
Circular Buffer | Circular Buffer Implementation in C
-
Video 8: Circular Buffer Memory Architecture for Reducing Power
-
Data Structures in Typescript #12 - Circular Buffer Implementation
-
11: Circular Buffers, C++ Real-Time Audio Programming with Bela
-
007 - Circular Buffer implementation in C
Transcription
Overview

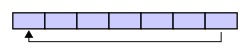
A circular buffer first starts out empty and has a set length. In the diagram below is a 7-element buffer:
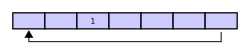
Assume that 1 is written in the center of a circular buffer (the exact starting location is not important in a circular buffer):
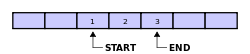
Then assume that two more elements are added to the circular buffer — 2 & 3 — which get put after 1:
If two elements are removed, the two oldest values inside of the circular buffer would be removed. Circular buffers use FIFO (first in, first out) logic. In the example, 1 & 2 were the first to enter the circular buffer, they are the first to be removed, leaving 3 inside of the buffer.
If the buffer has 7 elements, then it is completely full:
A property of the circular buffer is that when it is full and a subsequent write is performed, then it starts overwriting the oldest data. In the current example, two more elements — A & B — are added and they overwrite the 3 & 4:
Alternatively, the routines that manage the buffer could prevent overwriting the data and return an error or raise an exception. Whether or not data is overwritten is up to the semantics of the buffer routines or the application using the circular buffer.
Finally, if two elements are now removed then what would be returned is not 3 & 4 (or rather now A & B) but 5 & 6 because 5 & 6 are now the oldest elements, yielding the buffer with:
Uses
The useful property of a circular buffer is that it does not need to have its elements shuffled around when one is consumed. (If a non-circular buffer were used then it would be necessary to shift all elements when one is consumed.) In other words, the circular buffer is well-suited as a FIFO (first in, first out) buffer while a standard, non-circular buffer is well suited as a LIFO (last in, first out) buffer.
Circular buffering makes a good implementation strategy for a queue that has fixed maximum size. Should a maximum size be adopted for a queue, then a circular buffer is a completely ideal implementation; all queue operations are constant time. However, expanding a circular buffer requires shifting memory, which is comparatively costly. For arbitrarily expanding queues, a linked list approach may be preferred instead.
In some situations, overwriting circular buffer can be used, e.g. in multimedia. If the buffer is used as the bounded buffer in the producer–consumer problem then it is probably desired for the producer (e.g., an audio generator) to overwrite old data if the consumer (e.g., the sound card) is unable to momentarily keep up. Also, the LZ77 family of lossless data compression algorithms operates on the assumption that strings seen more recently in a data stream are more likely to occur soon in the stream. Implementations store the most recent data in a circular buffer.
Circular buffer mechanics
A circular buffer can be implemented using a pointer and three integers:[4]
- buffer start in memory
- buffer capacity (length)
- write to buffer index (end)
- read from buffer index (start)
This image shows a partially full buffer with Length = 7:
This image shows a full buffer with four elements (numbers 1 through 4) having been overwritten:
In the beginning the indexes end and start are set to 0. The circular buffer write operation writes an element to the end index position and the end index is incremented to the next buffer position. The circular buffer read operation reads an element from the start index position and the start index is incremented to the next buffer position.
The start and end indexes alone are not enough to distinguish between buffer full or empty state while also utilizing all buffer slots,[5] but can be if the buffer only has a maximum in-use size of Length - 1.[6] In this case, the buffer is empty if the start and end indexes are equal and full when the in-use size is Length - 1. Another solution is to have another integer count that is incremented at a write operation and decremented at a read operation. Then checking for emptiness means testing count equals 0 and checking for fullness means testing count equals Length.[7]
The following source code is a C implementation together with a minimal test. Function put() puts an item in the buffer, function get() gets an item from the buffer. Both functions take care about the capacity of the buffer :
#include <stdio.h>
enum { N = 10 }; // N elements of the circular buffer
int buffer [N];
int writeIndx = 0;
int readIndx = 0;
int put (int item)
{
if ((writeIndx + 1) % N == readIndx)
{
// buffer is full, avoid overflow
return 0;
}
buffer[writeIndx] = item;
writeIndx = (writeIndx + 1) % N;
return 1;
}
int get (int * value)
{
if (readIndx == writeIndx)
{
// buffer is empty
return 0;
}
*value = buffer[readIndx];
readIndx = (readIndx + 1) % N;
return 1;
}
int main ()
{
// test circular buffer
int value = 1001;
while (put (value ++));
while (get (& value))
printf ("read %d\n", value);
return 0;
}
Optimization
A circular-buffer implementation may be optimized by mapping the underlying buffer to two contiguous regions of virtual memory.[8][disputed ] (Naturally, the underlying buffer‘s length must then equal some multiple of the system’s page size.) Reading from and writing to the circular buffer may then be carried out with greater efficiency by means of direct memory access; those accesses which fall beyond the end of the first virtual-memory region will automatically wrap around to the beginning of the underlying buffer. When the read offset is advanced into the second virtual-memory region, both offsets—read and write—are decremented by the length of the underlying buffer.
Fixed-length-element and contiguous-block circular buffer
Perhaps the most common version of the circular buffer uses 8-bit bytes as elements.
Some implementations of the circular buffer use fixed-length elements that are bigger than 8-bit bytes—16-bit integers for audio buffers, 53-byte ATM cells for telecom buffers, etc. Each item is contiguous and has the correct data alignment, so software reading and writing these values can be faster than software that handles non-contiguous and non-aligned values.
Ping-pong buffering can be considered a very specialized circular buffer with exactly two large fixed-length elements.
The bip buffer (bipartite buffer) is very similar to a circular buffer, except it always returns contiguous blocks which can be variable length. This offers nearly all the efficiency advantages of a circular buffer while maintaining the ability for the buffer to be used in APIs that only accept contiguous blocks.[9]
Fixed-sized compressed circular buffers use an alternative indexing strategy based on elementary number theory to maintain a fixed-sized compressed representation of the entire data sequence.[10]
References
- ^ Arpaci-Dusseau, Remzi H.; Arpaci-Dusseau, Andrea C. (2014), Operating Systems: Three Easy Pieces [Chapter: Condition Variables, figure 30.13] (PDF), Arpaci-Dusseau Books
- ^ Hartl, Johann (17 October 2011). "Impulswiederholer - Telephone Exchange (video)". Youtube. Retrieved 15 December 2021.
- ^ Fraser, Alexander Gibson. "US patent 3979733 Digital data communications system packet switch". US States Patent. Retrieved 15 December 2021.
- ^ Liu, Z.; Wu, F.; Das, S.K. (2021). Wireless Algorithms, Systems, and Applications: 16th International Conference, WASA 2021, Nanjing, China, June 25–27, 2021, Proceedings, Part II. Lecture Notes in Computer Science. Springer International Publishing. p. 117. ISBN 978-3-030-86130-8. Retrieved 2023-09-04.
- ^ Chandrasekaran, Siddharth (2014-05-16). "Implementing Circular/Ring Buffer in Embedded C". Embed Journal. EmbedJournal Team. Archived from the original on 11 February 2017. Retrieved 14 August 2017.
- ^ Circular buffers kernel.org
- ^ Morin, Pat. "ArrayQueue: An Array-Based Queue". Open Data Structures (in pseudocode). Archived from the original on 31 August 2015. Retrieved 7 November 2015.
- ^ Mike Ash (2012-02-17). "mikeash.com: Friday Q&A 2012-02-17: Ring Buffers and Mirrored Memory: Part II". mikeash.com. Archived from the original on 2019-01-11. Retrieved 2019-01-10.
- ^ Simon Cooke (2003), "The Bip Buffer - The Circular Buffer with a Twist"
- ^ Gunther, John C. (March 2014). "Algorithm 938: Compressing circular buffers". ACM Transactions on Mathematical Software. 40 (2): 1–12. doi:10.1145/2559995. S2CID 14682572.
External links
- CircularBuffer at the Portland Pattern Repository
- Boost:
- CB in Linux kernel
- CB in DSP
- Circular queue in C Archived 2018-10-29 at the Wayback Machine