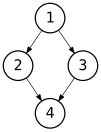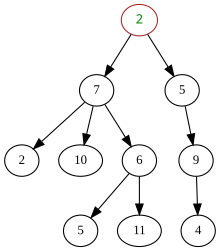
In computer science, a tree is a widely used abstract data type that represents a hierarchical tree structure with a set of connected nodes. Each node must be connected to exactly one parent. and it can be connected to one or many children (depending on the type of tree).[1] The root node, which has no parent (i.e., the root node as the top-most node in the tree hierarchy). These constraints mean there are no cycles or "loops" (no node can be its own ancestor), and also that each child can be treated like the root node of its own subtree, making recursion a useful technique for tree traversal. In contrast to linear data structures, many trees cannot be represented by relationships between neighboring nodes (parent and children nodes of a node under consideration if they exists) in a single straight line (called edge or link between two adjacent nodes).
Binary trees are a commonly used type, which constrain the number of children for each parent to at most two. When the order of the children is specified, this data structure corresponds to an ordered tree in graph theory. A value or pointer to other data may be associated with every node in the tree, or sometimes only with the leaf nodes, which have no children nodes.
The abstract data type (ADT) can be represented in a number of ways, including a list of parents with pointers to children, a list of children with pointers to parents, or a list of nodes and a separate list of parent-child relations (a specific type of adjacency list). Representations might also be more complicated, for example using indexes or ancestor lists for performance.
Trees as used in computing are similar to but can be different from mathematical constructs of trees in graph theory, trees in set theory, and trees in descriptive set theory.
YouTube Encyclopedic
-
1/5Views:1 419 524259 294986 085948 184543 821
-
Data structures: Introduction to Trees
-
Introduction to Trees (Data Structures & Algorithms #9)
-
5.1 Tree in Data Structure | Introduction to Trees | Data Structures Tutorials
-
Data Structures: Trees
-
Binary Tree Algorithms for Technical Interviews - Full Course
Transcription
Hello everyone ! In this lesson, we will introduce you to an interesting data structure that has got its application in a wide number of scenarios in computer science and this data structure is tree. So, far in this series, we have talked about what we can call linear data structures. Array, Linked List, stack and queue, all of these are linear data structures. All of these are basically collections of different kinds in which data is arranged in a sequential manner. In all these structures that I am showing here, we have a logical start and a logical end and then an element in any of these collections can have a next element and e previous element. So, all in all we have linear or sequential arrangement. Now, as we understand, these data structures are ways to store and organize data in computers. For different kinds of data, we use different kinds of data structure. Our choice of data structure depends upon a number of factors. First of all, its about what needs to be stored. A certain data structure can be best fit for a particular kind of data. Then, we may care for the cost of operations. Quite often, we want to minimize the cost of most frequently performed operations. For example, lets say we have a simple list and we are searching for an element in the list most of the time. Then, we may want to store the list or collection as an array in sorted order, so we can perform something like binary search really fast. Another factor can be memory consumption. Sometimes, we may want to minimize the memory usage and finally we may also choose a data structure for ease of implementation, although this may not be the best strategy. Tree is one data structure that's quite often used to represent hierarchical data. For example, lets say we want to show employees in an organization and their positions in organizational hierarchy, then we can show it something like this. Lets say this is organization hierarchy of some company. In this company, John is CEO and john has two direct reports - Steve and Rama. Then Steve has 3 direct reports. Steve is manager of Lee, Bob and Ella. They may be having some designation. Rama also has two direct reports. Then Bob has two direct reports and then Tom has 1 direct report. This particular logical structure that I have drawn here is a Tree. Well, you have to look at this structure upside down and then it will resemble a real tree. The root here is at top and we are branching out in downward direction. Logical representation of tree data structure is always like this. Root at top and branching out in downward direction. Ok, so tree is an efficient way of storing and organizing data that is naturally hierarchical, but this is not the only application of tree in computer science. We will talk about other applications and some of the implementation details like how we can create such a logical structure in computer's memory later. First I want to define tree as a logical model. Tree data structure can be defined as a collection of entities called nodes linked together to simulate hierarchy. Tree is a non-linear data structure. Its a hierarchical structure. The topmost node in the tree is called root of the tree. Each node will contain some data and this can be data of any type. In the tree that I am showing in right here data is name of employee and designation. So, we can have an object with two string fields one to store name and another to store designation. Okay, so each node will contain some data and may contain link or reference to some other nodes that can be called its children. Now I am introducing you to some vocabulary that we use for tree data structure. What I am going to do here is , I am going to number these Nodes in the left tree. So, I can refer to these Nodes using these numbers. I am numbering these nodes only for my convenience. its not to show any order. Ok, coming back, as i had said each node will have some data. We call fill in some data in these circles. It can be data of any type. it can be an integer or a character or a string or we can simple assume that there is some data filled inside these nodes and we are not showing it. Ok, as we were discussing, a node may have link or reference to some other nodes that will be called its children. Each arrow in this structure here is a link. Ok, now as you can see, the root node which is numbered 1 by me and once again this number is not indicative of any order. I could have called the root node number 10 also. So, root node has link to these two nodes numbered 2 and 3. So, 2 and 3 will be called children of 1 and node 1 will be called parent of nodes 2 and 3. I'll write down all these terms that I am talking about. We mentioned root, children and parent. In this tree, one is a parent of , 1 is parent of 2 and 3. 2 is child of 1. And now, 4 , 5 and 6 are children of 2. So, node 2 is child of node 1, but parent of nodes 4, 5 and 6. Children of same parent are called sibling. I am showing siblings in same color here. 2 and 3 are sibling. Then, 4, 5 and 6 are sibling, then 7,8 are sibling and finally 9 and 10 are sibling. I hope you are clear with these terms now. The topmost node in the tree is called root. Root would be the only node without a parent. And then, if a node has a direct link to some other node, then we have a parent child relationship between the nodes. Any node in the tree that does not have a child is called leaf node. All these nodes marked in black here are leaves. So, leaf is one more term. All other nodes with at least one child can be called internal nodes. And we can have some more relationships like parent of parent can be called grand-parent. So, 1 is grand-parent of 4 and 4 is grand-child of 1. In general, if we can go from node A to B walking through the links and remember these links are not bidirectional. We have a link from 1 to 2, so we can go from 1 to 2, but we cannot go from 2 to 1. When we are walking the tree, we can walk in only one direction. OK, so if we can go from node A to node B, then A can be called ancestor of B and B can be called descendant of A. Lets pick up this node numbered 10. 1, 2 and 5 are all ancestors of 10 and 10 is a descendant of all of these nodes. We can walk from any of these nodes to 10. Ok, let me now ask you some questions to make sure you understand things. What are the common ancestors of 4 and 9? Ancestors of 4 are 1 and 2 and ancestors of 9 are 1,2 and 5. So, common ancestors will be 1 and 2. Ok, next question. Are 6 and 7 sibling? Sibling must have same parent. 6 and 7 do not have same parent. They have same grand-parent. one is grandparent of both. Nodes not having same parent but having same grandparent can be called cousins. So, 6 and 7 are cousins. These relationships are really interesting. We can also say that node number 3 is uncle of node number 6 because its sibling of 2 which is father of 6 or i should say parent of 6. So, we have quite some terms in vocabulary of tree. Ok, now I will talk about some properties of tree. Tree can be called a recursive data structure. We can define tree recursively as a structure that consists of a distinguished node called root and some sub-trees and the arrangement is such that root of the tree contains link to roots of all the sub-trees. T1, T2 and T3 in this figure are sub-trees. In the tree that I have drawn in left here, we have 2 sub-trees for root node. I am showing the root node in red, the left sub-tree in brown and right sub-tree in yellow. We can further split the left sub-tree and look at it like node number 2 is root of this sub-tree and this particular tree with node number 2 as root has 3 sub-trees. i am showing the three sub-trees in 3 different colors. Recursion basically is reducing something in a self similar manner. This recursive property of tree will be used everywhere in all implementation and usage of tree. The next property that I want to talk about is - in a tree with n nodes, there will be exactly n-1 links or edges. Each arrow in this figure can be called a link or an edge. All nodes except the root node will have exactly 1 incoming edge. If you can see, I'll pick this node numbered 2. There is only one incoming link. This is incoming link and these three are outgoing links. There will be one link for each parent-child relationship. So, in a valid tree if there are n nodes, there will be exactly n-1 edges. One incoming edge for each node except the root. Ok, now i want to talk about these two properties called depth and height. Depth of some node X in a tree can be defined as length of the path from root to Node X. Each edge in the path will contribute one unit to the length. So, we can also say number of edges in path from root to X. The depth of root node will be zero. Lets pick some other node. For this node, numbered 5, we have 2 edges in the path from root. So, the depth of this node is 2. In this tree here, depth of nodes 2 and 3 is 1. Depth of nodes 4,5,6,7 and 8 is 2 and the depth of nodes 9, 10 and 11 is 3. Ok, now height of a node in tree can be defined as number of edges in longest path from that node to a leaf node. So, height of some node X will be equal to number of edges in longest path from X to a leaf. In this figure, for node 3, the longest path from this node to any leaf is 2. So, height of node 3 is 2. Node 8 is also a leaf node. I'll mark all the leaf nodes here. A leaf node is a node with zero child. The longest path from node 3 to any of the leaf nodes is 2. So, the height of Node 3 is 2. Height of leaf nodes will be 0. So, what will be the height of root node in this tree. We can reach all the leaves from root node. number of edges in longest path is 3. So, height of the root node here is 3. We also define height of a tree. Height of tree is defined as height of root node. Height of this tree that I am showing here is 3. Height and depth are different properties and height and depth of a node may or may not be same. We often confuse between the two. Based on properties, trees are classified into various categories. There are different kinds of trees that are used in different scenarios. Simplest and most common kind of tree is a tree with this property that any node can have at most 2 children. In this figure, node 2 has 3 children. I am getting rid of some nodes and now this is a binary tree. Binary tree is most famous and throughout this series, we will mostly be talking about binary trees. The most common way of implementing tree is dynamically created nodes linked using pointers or references, just the way we do for linked list. We can look at the tree like this. in this structure that I have drawn in right here, node has 3 fields. one of the fields is to store data. Lets say middle cell is to store data. The left cell is to store the address of the left child. And the right cell is to store address of right child. Because this is a binary tree, we cannot have more than two children. We can all one of the children left child and another right child. Programmatically, in C or C++, we can define a node as a structure like this. We have three fields here - one to store data, lets say data type is integer. I have filled in some data in these nodes. So, in each node, we have 3 fields. We have an integer variable to store the data and then we have 2 pointers to Node, one to store the address of the left child that will be the root of the left sub-tree and another to store the address of the right child. We have kept only 2 pointers because we can have at most 2 children in binary tree. This particular definition of Node can be used only for a binary tree. For generic trees that can have any number of children, we use some other structure and I'll talk about it in later lessons. In fact, we will discuss implementation in detail in later lessons. This is just to give you a brief idea of how things will be like in implementation. Ok, so this is cool. We understand what a tree data structure is, but in the beginning we had said that storing naturally hierarchical data is not the only application of tree. So, lets quickly have a look at some of the applications of tree in computer science. First application of course is storing naturally hierarchical data. For example, the file system on your disc drive, the file and folder hierarchy is naturally hierarchical data. its stored in the form of tree. Next application is organizing data, organizing collections for quick search, insertion and deletion. For example, binary search tree that we'll be discussing a lot in next couple of lessons can give us order of log N time for searching an element in it. A special kind of tree called Trie is used , is use to store dictionary. Its really fast and efficient and is used for dynamic spell checking. Tree data structure is also used in network routing algorithms and this list goes on. We'll talk about different kinds of trees and their applications in later lessons. I'll stop here now. This is good for an introduction. In next couple of lessons, we will talk about binary search trees and its implementation. This is it for this lesson. Thanks for watching !
Applications
Trees are commonly used to represent or manipulate hierarchical data in applications such as:
- File systems for:
- Directory structure used to organize subdirectories and files (symbolic links create non-tree graphs, as do multiple hard links to the same file or directory)
- The mechanism used to allocate and link blocks of data on the storage device
- Class hierarchy or "inheritance tree" showing the relationships among classes in object-oriented programming; multiple inheritance produces non-tree graphs
- Abstract syntax trees for computer languages
- Natural language processing:
- Parse trees
- Modeling utterances in a generative grammar
- Dialogue tree for generating conversations
- Document Object Models ("DOM tree") of XML and HTML documents
- Search trees store data in a way that makes an efficient search algorithm possible via tree traversal
- A binary search tree is a type of binary tree
- Representing sorted lists of data
- Computer-generated imagery:
- Storing Barnes–Hut trees used to simulate galaxies
- Implementing heaps
- Nested set collections
- Hierarchical taxonomies such as the Dewey Decimal Classification with sections of increasing specificity.
- Hierarchical temporal memory
- Genetic programming
- Hierarchical clustering
Trees can be used to represent and manipulate various mathematical structures, such as:
- Paths through an arbitrary node-and-edge graph (including multigraphs), by making multiple nodes in the tree for each graph node used in multiple paths
- Any mathematical hierarchy
Tree structures are often used for mapping the relationships between things, such as:
- Components and subcomponents which can be visualized in an exploded-view drawing
- Subroutine calls used to identify which subroutines in a program call other subroutines non recursively
- Inheritance of DNA among species by evolution, of source code by software projects (e.g. Linux distribution timeline), of designs in various types of cars, etc.
- The contents of hierarchical namespaces
JSON and YAML documents can be thought of as trees, but are typically represented by nested lists and dictionaries.
Terminology
A node is a structure which may contain data and connections to other nodes, sometimes called edges or links. Each node in a tree has zero or more child nodes, which are below it in the tree (by convention, trees are drawn with descendants going downwards). A node that has a child is called the child's parent node (or superior). All nodes have exactly one parent, except the topmost root node, which has none. A node might have many ancestor nodes, such as the parent's parent. Child nodes with the same parent are sibling nodes. Typically siblings have an order, with the first one conventionally drawn on the left. Some definitions allow a tree to have no nodes at all, in which case it is called empty.
An internal node (also known as an inner node, inode for short, or branch node) is any node of a tree that has child nodes. Similarly, an external node (also known as an outer node, leaf node, or terminal node) is any node that does not have child nodes.
The height of a node is the length of the longest downward path to a leaf from that node. The height of the root is the height of the tree. The depth of a node is the length of the path to its root (i.e., its root path). Thus the root node has depth zero, leaf nodes have height zero, and a tree with only a single node (hence both a root and leaf) has depth and height zero. Conventionally, an empty tree (tree with no nodes, if such are allowed) has height −1.
Each non-root node can be treated as the root node of its own subtree, which includes that node and all its descendants.[a][2]
Other terms used with trees:
- Neighbor
- Parent or child.
- Ancestor
- A node reachable by repeated proceeding from child to parent.
- Descendant
- A node reachable by repeated proceeding from parent to child. Also known as subchild.
- Degree
- For a given node, its number of children. A leaf, by definition, has degree zero.
- Degree of tree
- The degree of a tree is the maximum degree of a node in the tree.
- Distance
- The number of edges along the shortest path between two nodes.
- Level
- The level of a node is the number of edges along the unique path between it and the root node.[3] This is the same as depth.
- Width
- The number of nodes in a level.
- Breadth
- The number of leaves.
- Forest
- A set of one or more disjoint trees.
- Ordered tree
- A rooted tree in which an ordering is specified for the children of each vertex.
- Size of a tree
- Number of nodes in the tree.
Examples of trees and non-trees
Common operations
- Enumerating all the items
- Enumerating a section of a tree
- Searching for an item
- Adding a new item at a certain position on the tree
- Deleting an item
- Pruning: Removing a whole section of a tree
- Grafting: Adding a whole section to a tree
- Finding the root for any node
- Finding the lowest common ancestor of two nodes
Traversal and search methods
Stepping through the items of a tree, by means of the connections between parents and children, is called walking the tree, and the action is a walk of the tree. Often, an operation might be performed when a pointer arrives at a particular node. A walk in which each parent node is traversed before its children is called a pre-order walk; a walk in which the children are traversed before their respective parents are traversed is called a post-order walk; a walk in which a node's left subtree, then the node itself, and finally its right subtree are traversed is called an in-order traversal. (This last scenario, referring to exactly two subtrees, a left subtree and a right subtree, assumes specifically a binary tree.) A level-order walk effectively performs a breadth-first search over the entirety of a tree; nodes are traversed level by level, where the root node is visited first, followed by its direct child nodes and their siblings, followed by its grandchild nodes and their siblings, etc., until all nodes in the tree have been traversed.
Representations
There are many different ways to represent trees. In working memory, nodes are typically dynamically allocated records with pointers to their children, their parents, or both, as well as any associated data. If of a fixed size, the nodes might be stored in a list. Nodes and relationships between nodes might be stored in a separate special type of adjacency list. In relational databases, nodes are typically represented as table rows, with indexed row IDs facilitating pointers between parents and children.
Nodes can also be stored as items in an array, with relationships between them determined by their positions in the array (as in a binary heap).
A binary tree can be implemented as a list of lists: the head of a list (the value of the first term) is the left child (subtree), while the tail (the list of second and subsequent terms) is the right child (subtree). This can be modified to allow values as well, as in Lisp S-expressions, where the head (value of first term) is the value of the node, the head of the tail (value of second term) is the left child, and the tail of the tail (list of third and subsequent terms) is the right child.
Ordered trees can be naturally encoded by finite sequences, for example with natural numbers.[4]
Type theory
As an abstract data type, the abstract tree type T with values of some type E is defined, using the abstract forest type F (list of trees), by the functions:
- value: T → E
- children: T → F
- nil: () → F
- node: E × F → T
with the axioms:
- value(node(e, f)) = e
- children(node(e, f)) = f
In terms of type theory, a tree is an inductive type defined by the constructors nil (empty forest) and node (tree with root node with given value and children).
Mathematical terminology
Viewed as a whole, a tree data structure is an ordered tree, generally with values attached to each node. Concretely, it is (if required to be non-empty):
- A rooted tree with the "away from root" direction (a more narrow term is an "arborescence"), meaning:
- A directed graph,
- whose underlying undirected graph is a tree (any two vertices are connected by exactly one simple path),
- with a distinguished root (one vertex is designated as the root),
- which determines the direction on the edges (arrows point away from the root; given an edge, the node that the edge points from is called the parent and the node that the edge points to is called the child), together with:
- an ordering on the child nodes of a given node, and
- a value (of some data type) at each node.
Often trees have a fixed (more properly, bounded) branching factor (outdegree), particularly always having two child nodes (possibly empty, hence at most two non-empty child nodes), hence a "binary tree".
Allowing empty trees makes some definitions simpler, some more complicated: a rooted tree must be non-empty, hence if empty trees are allowed the above definition instead becomes "an empty tree or a rooted tree such that ...". On the other hand, empty trees simplify defining fixed branching factor: with empty trees allowed, a binary tree is a tree such that every node has exactly two children, each of which is a tree (possibly empty).
See also
- Tree structure (general)
- Category:Trees (data structures) (catalogs types of computational trees)
Notes
- ^ This is different from the formal definition of subtree used in graph theory, which is a subgraph that forms a tree – it need not include all descendants. For example, the root node by itself is a subtree in the graph theory sense, but not in the data structure sense (unless there are no descendants).
References
- ^ Subero, Armstrong (2020). "3. Tree Data Structure". Codeless Data Structures and Algorithms. Berkeley, CA: Apress. doi:10.1007/978-1-4842-5725-8. ISBN 978-1-4842-5724-1.
A parent can have multiple child nodes. ... However, a child node cannot have multiple parents. If a child node has multiple parents, then it is what we call a graph.
- ^ Weisstein, Eric W. "Subtree". MathWorld.
- ^ Susanna S. Epp (Aug 2010). Discrete Mathematics with Applications. Pacific Grove, CA: Brooks/Cole Publishing Co. p. 694. ISBN 978-0-495-39132-6.
- ^ L. Afanasiev; P. Blackburn; I. Dimitriou; B. Gaiffe; E. Goris; M. Marx; M. de Rijke (2005). "PDL for ordered trees" (PDF). Journal of Applied Non-Classical Logics. 15 (2): 115–135. doi:10.3166/jancl.15.115-135. S2CID 1979330.
Further reading
- Donald Knuth. The Art of Computer Programming: Fundamental Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89683-4 . Section 2.3: Trees, pp. 308–423.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 10.4: Representing rooted trees, pp. 214–217. Chapters 12–14 (Binary Search Trees, Red–Black Trees, Augmenting Data Structures), pp. 253–320.