Brahmagupta theorem

In geometry, Brahmagupta's theorem states that if a cyclic quadrilateral is orthodiagonal (that is, has perpendicular diagonals), then the perpendicular to a side from the point of intersection of the diagonals always bisects the opposite side.^[1] It is named after the Indian mathematician Brahmagupta (598-668).^[2]

More specifically, let A, B, C and D be four points on a circle such that the lines AC and BD are perpendicular. Denote the intersection of AC and BD by M. Drop the perpendicular from M to the line BC, calling the intersection E. Let F be the intersection of the line EM and the edge AD. Then, the theorem states that F is the midpoint AD.

Proof

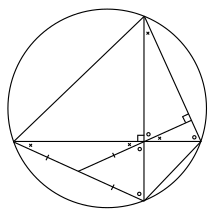
We need to prove that AF = FD. We will prove that both AF and FD are in fact equal to FM.

To prove that AF = FM, first note that the angles FAM and CBM are equal, because they are inscribed angles that intercept the same arc of the circle (CD). Furthermore, the angles CBM and CME are both complementary to angle BCM (i.e., they add up to 90°), and are therefore equal. Finally, the angles CME and FMA are the same. Hence, AFM is an isosceles triangle, and thus the sides AF and FM are equal.

The proof that FD = FM goes similarly: the angles FDM, BCM, BME and DMF are all equal, so DFM is an isosceles triangle, so FD = FM. It follows that AF = FD, as the theorem claims.

See also

• Brahmagupta's formula for the area of a cyclic quadrilateral

References

External links

• Brahmagupta theorem at ProofWiki
• Brahmagupta's Theorem at cut-the-knot
• Weisstein, Eric W. "Brahmagupta's theorem". MathWorld.

This page was last edited on 16 March 2024, at 16:28