Baranyai's theorem

In combinatorial mathematics, Baranyai's theorem (proved by and named after Zsolt Baranyai) deals with the decompositions of complete hypergraphs.

Statement of the theorem

The statement of the result is that if ${\displaystyle 2\leq r<k}$ are integers and r divides k, then the complete hypergraph ${\displaystyle K_{r}^{k}}$ decomposes into 1-factors. ${\displaystyle K_{r}^{k}}$ is a hypergraph with k vertices, in which every subset of r vertices forms a hyperedge; a 1-factor of this hypergraph is a set of hyperedges that touches each vertex exactly once, or equivalently a partition of the vertices into subsets of size r. Thus, the theorem states that the k vertices of the hypergraph may be partitioned into subsets of r vertices in ${\displaystyle {\binom {k}{r}}{\frac {r}{k}}={\binom {k-1}{r-1}}}$ different ways, in such a way that each r-element subset appears in exactly one of the partitions.

The case ${\displaystyle r=2}$

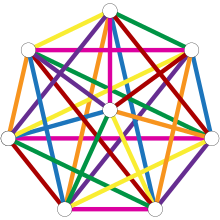
In the special case ${\displaystyle r=2}$, we have a complete graph ${\displaystyle K_{n}}$ on ${\displaystyle n}$ vertices, and we wish to color the edges with ${\displaystyle {\binom {n}{2}}{\frac {2}{n}}=n-1}$ colors so that the edges of each color form a perfect matching. Baranyai's theorem says that we can do this whenever ${\displaystyle n}$ is even.

History

The r = 2 case can be rephrased as stating that every complete graph with an even number of vertices has an edge coloring whose number of colors equals its degree, or equivalently that its edges may be partitioned into perfect matchings. It may be used to schedule round-robin tournaments, and its solution was already known in the 19th century. The case that k = 2r is also easy.

The r = 3 case was established by R. Peltesohn in 1936. The general case was proved by Zsolt Baranyai in 1975.

References

• Baranyai, Zs. (1975), "On the factorization of the complete uniform hypergraph", in Hajnal, A.; Rado, R.; Sós, V. T. (eds.), Infinite and Finite Sets, Proc. Coll. Keszthely, 1973, Colloquia Math. Soc. János Bolyai, vol. 10, North-Holland, pp. 91–107.
• van Lint, J. H.; Wilson, R. M. (2001), A Course in Combinatorics (2nd ed.), Cambridge University Press.
• Peltesohn, R. (1936), Das Turnierproblem für Spiele zu je dreien, Inaugural dissertation, Berlin{{citation}}: CS1 maint: location missing publisher (link).

This page was last edited on 12 January 2023, at 22:48