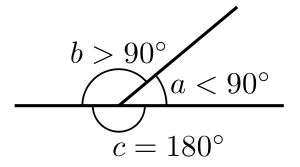In Euclidean geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.[1] Angles formed by two rays are also known as plane angles as they lie in the plane that contains the rays. Angles are also formed by the intersection of two planes; these are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection.
The magnitude of an angle is called an angular measure or simply "angle". Angle of rotation is a measure conventionally defined as the ratio of a circular arc length to its radius, and may be a negative number. In the case of a geometric angle, the arc is centered at the vertex and delimited by the sides. In the case of a rotation, the arc is centered at the center of the rotation and delimited by any other point and its image by the rotation.
YouTube Encyclopedic
-
1/5Views:4 805 2801 086 0612 604 539253 15530 167
-
Math Antics - Angle Basics
-
Angles: measuring angles and their names! | Educational Videos for Kids
-
Math Antics - Angles & Degrees
-
GCSE Maths - Alternate, Corresponding and Allied Angles - Parallel Lines Angle Rules #117
-
Types of Angles (Acute, Obtuse, Right, Straight, Reflex) | Math with Mr. J
Transcription
History and etymology
The word angle comes from the Latin word angulus, meaning "corner". Cognate words include the Greek ἀγκύλος (ankylοs) meaning "crooked, curved" and the English word "ankle". Both are connected with the Proto-Indo-European root *ank-, meaning "to bend" or "bow".[2]
Euclid defines a plane angle as the inclination to each other, in a plane, of two lines that meet each other and do not lie straight with respect to each other. According to the Neoplatonic metaphysician Proclus, an angle must be either a quality, a quantity, or a relationship. The first concept, angle as quality, was used by Eudemus of Rhodes, who regarded an angle as a deviation from a straight line; the second, angle as quality, by Carpus of Antioch, who regarded it as the interval or space between the intersecting lines; Euclid adopted the third: angle as a relationship.[3]
Identifying angles
In mathematical expressions, it is common to use Greek letters (α, β, γ, θ, φ, . . . ) as variables denoting the size of some angle[4] (the symbol π is typically not used for this purpose to avoid confusion with the constant denoted by that symbol). Lower case Roman letters (a, b, c, . . . ) are also used. In contexts where this is not confusing, an angle may be denoted by the upper case Roman letter denoting its vertex. See the figures in this article for examples.
The three defining points may also identify angles in geometric figures. For example, the angle with vertex A formed by the rays AB and AC (that is, the half-lines from point A through points B and C) is denoted ∠BAC or . Where there is no risk of confusion, the angle may sometimes be referred to by a single vertex alone (in this case, "angle A").
In other ways, an angle denoted as, say, ∠BAC might refer to any of four angles: the clockwise angle from B to C about A, the anticlockwise angle from B to C about A, the clockwise angle from C to B about A, or the anticlockwise angle from C to B about A, where the direction in which the angle is measured determines its sign (see § Signed angles). However, in many geometrical situations, it is evident from the context that the positive angle less than or equal to 180 degrees is meant, and in these cases, no ambiguity arises. Otherwise, to avoid ambiguity, specific conventions may be adopted so that, for instance, ∠BAC always refers to the anticlockwise (positive) angle from B to C about A and ∠CAB the anticlockwise (positive) angle from C to B about A.
Types of angles
Individual angles
There is some common terminology for angles, whose measure is always non-negative (see § Signed angles):
- An angle equal to 0° or not turned is called a zero angle.[5]
- An angle smaller than a right angle (less than 90°) is called an acute angle[6] ("acute" meaning "sharp").
- An angle equal to 1/4 turn (90° or π/2 radians) is called a right angle. Two lines that form a right angle are said to be normal, orthogonal, or perpendicular.[7]
- An angle larger than a right angle and smaller than a straight angle (between 90° and 180°) is called an obtuse angle[6] ("obtuse" meaning "blunt").
- An angle equal to 1/2 turn (180° or π radians) is called a straight angle.[5]
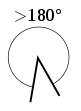
- An angle larger than a straight angle but less than 1 turn (between 180° and 360°) is called a reflex angle.
- An angle equal to 1 turn (360° or 2π radians) is called a full angle, complete angle, round angle or perigon.
- An angle that is not a multiple of a right angle is called an oblique angle.
The names, intervals, and measuring units are shown in the table below:
| Name | zero angle | acute angle | right angle | obtuse angle | straight angle | reflex angle | perigon | |||
| Unit | Interval | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| turn | 0 turn | (0, 1/4) turn | 1/4 turn | (1/4, 1/2) turn | 1/2 turn | (1/2, 1) turn | 1 turn | |||
| radian | 0 rad | (0, 1/2π) rad | 1/2π rad | (1/2π, π) rad | π rad | (π, 2π) rad | 2π rad | |||
| degree | 0° | (0, 90)° | 90° | (90, 180)° | 180° | (180, 360)° | 360° | |||
| gon | 0g | (0, 100)g | 100g | (100, 200)g | 200g | (200, 400)g | 400g | |||
Vertical and adjacent angle pairs

When two straight lines intersect at a point, four angles are formed. Pairwise, these angles are named according to their location relative to each other.
- A pair of angles opposite each other, formed by two intersecting straight lines that form an "X"-like shape, are called vertical angles or opposite angles or vertically opposite angles. They are abbreviated as vert. opp. ∠s.[8]
The equality of vertically opposite angles is called the vertical angle theorem. Eudemus of Rhodes attributed the proof to Thales of Miletus.[9][10] The proposition showed that since both of a pair of vertical angles are supplementary to both of the adjacent angles, the vertical angles are equal in measure. According to a historical note,[10] when Thales visited Egypt, he observed that whenever the Egyptians drew two intersecting lines, they would measure the vertical angles to make sure that they were equal. Thales concluded that one could prove that all vertical angles are equal if one accepted some general notions such as:
- All straight angles are equal.
- Equals added to equals are equal.
- Equals subtracted from equals are equal.
When two adjacent angles form a straight line, they are supplementary. Therefore, if we assume that the measure of angle A equals x, the measure of angle C would be 180° − x. Similarly, the measure of angle D would be 180° − x. Both angle C and angle D have measures equal to 180° − x and are congruent. Since angle B is supplementary to both angles C and D, either of these angle measures may be used to determine the measure of Angle B. Using the measure of either angle C or angle D, we find the measure of angle B to be 180° − (180° − x) = 180° − 180° + x = x. Therefore, both angle A and angle B have measures equal to x and are equal in measure.
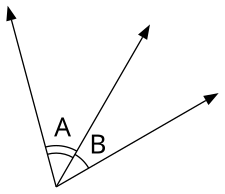
Angles A and B are adjacent. - Adjacent angles, often abbreviated as adj. ∠s, are angles that share a common vertex and edge but do not share any interior points. In other words, they are angles side by side or adjacent, sharing an "arm". Adjacent angles which sum to a right angle, straight angle, or full angle are special and are respectively called complementary, supplementary, and explementary angles (see § Combining angle pairs below).
A transversal is a line that intersects a pair of (often parallel) lines and is associated with exterior angles, interior angles, alternate exterior angles, alternate interior angles, corresponding angles, and consecutive interior angles.[11]
Combining angle pairs
The angle addition postulate states that if B is in the interior of angle AOC, then
I.e., the measure of the angle AOC is the sum of the measure of angle AOB and the measure of angle BOC.
Three special angle pairs involve the summation of angles:

- Complementary angles are angle pairs whose measures sum to one right angle (1/4 turn, 90°, or π/2 radians).[12] If the two complementary angles are adjacent, their non-shared sides form a right angle. In Euclidean geometry, the two acute angles in a right triangle are complementary because the sum of internal angles of a triangle is 180 degrees, and the right angle accounts for 90 degrees.
The adjective complementary is from the Latin complementum, associated with the verb complere, "to fill up". An acute angle is "filled up" by its complement to form a right angle.
The difference between an angle and a right angle is termed the complement of the angle.[13]
If angles A and B are complementary, the following relationships hold:
(The tangent of an angle equals the cotangent of its complement, and its secant equals the cosecant of its complement.)
The prefix "co-" in the names of some trigonometric ratios refers to the word "complementary".
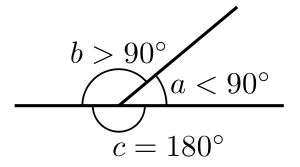
The angles a and b are supplementary angles. - Two angles that sum to a straight angle (1/2 turn, 180°, or π radians) are called supplementary angles.[14]
If the two supplementary angles are adjacent (i.e., have a common vertex and share just one side), their non-shared sides form a straight line. Such angles are called a linear pair of angles.[15] However, supplementary angles do not have to be on the same line and can be separated in space. For example, adjacent angles of a parallelogram are supplementary, and opposite angles of a cyclic quadrilateral (one whose vertices all fall on a single circle) are supplementary.
If a point P is exterior to a circle with center O, and if the tangent lines from P touch the circle at points T and Q, then ∠TPQ and ∠TOQ are supplementary.
The sines of supplementary angles are equal. Their cosines and tangents (unless undefined) are equal in magnitude but have opposite signs.
In Euclidean geometry, any sum of two angles in a triangle is supplementary to the third because the sum of the internal angles of a triangle is a straight angle.
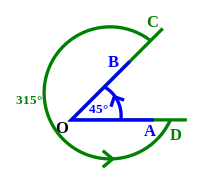
Angles AOB and COD are conjugate as they form a complete angle. Considering magnitudes, 45° + 315° = 360°. - Two angles that sum to a complete angle (1 turn, 360°, or 2π radians) are called explementary angles or conjugate angles.[16]
The difference between an angle and a complete angle is termed the explement of the angle or conjugate of an angle.

- An angle that is part of a simple polygon is called an interior angle if it lies on the inside of that simple polygon. A simple concave polygon has at least one interior angle, that is, a reflex angle. In Euclidean geometry, the measures of the interior angles of a triangle add up to π radians, 180°, or 1/2 turn; the measures of the interior angles of a simple convex quadrilateral add up to 2π radians, 360°, or 1 turn. In general, the measures of the interior angles of a simple convex polygon with n sides add up to (n − 2)π radians, or (n − 2)180 degrees, (n − 2)2 right angles, or (n − 2)1/2 turn.
- The supplement of an interior angle is called an exterior angle; that is, an interior angle and an exterior angle form a linear pair of angles. There are two exterior angles at each vertex of the polygon, each determined by extending one of the two sides of the polygon that meet at the vertex; these two angles are vertical and hence are equal. An exterior angle measures the amount of rotation one must make at a vertex to trace the polygon.[17] If the corresponding interior angle is a reflex angle, the exterior angle should be considered negative. Even in a non-simple polygon, it may be possible to define the exterior angle. Still, one will have to pick an orientation of the plane (or surface) to decide the sign of the exterior angle measure. In Euclidean geometry, the sum of the exterior angles of a simple convex polygon, if only one of the two exterior angles is assumed at each vertex, will be one full turn (360°). The exterior angle here could be called a supplementary exterior angle. Exterior angles are commonly used in Logo Turtle programs when drawing regular polygons.
- In a triangle, the bisectors of two exterior angles and the bisector of the other interior angle are concurrent (meet at a single point).[18]: 149
- In a triangle, three intersection points, each of an external angle bisector with the opposite extended side, are collinear.[18]: p. 149
- In a triangle, three intersection points, two between an interior angle bisector and the opposite side, and the third between the other exterior angle bisector and the opposite side extended are collinear.[18]: 149
- Some authors use the name exterior angle of a simple polygon to mean the explement exterior angle (not supplement!) of the interior angle.[19] This conflicts with the above usage.
- The angle between two planes (such as two adjacent faces of a polyhedron) is called a dihedral angle.[13] It may be defined as the acute angle between two lines normal to the planes.
- The angle between a plane and an intersecting straight line is equal to ninety degrees minus the angle between the intersecting line and the line that goes through the point of intersection and is normal to the plane.
Measuring angles
The size of a geometric angle is usually characterized by the magnitude of the smallest rotation that maps one of the rays into the other. Angles of the same size are said to be equal congruent or equal in measure.
In some contexts, such as identifying a point on a circle or describing the orientation of an object in two dimensions relative to a reference orientation, angles that differ by an exact multiple of a full turn are effectively equivalent. In other contexts, such as identifying a point on a spiral curve or describing an object's cumulative rotation in two dimensions relative to a reference orientation, angles that differ by a non-zero multiple of a full turn are not equivalent.
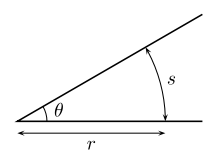
To measure an angle θ, a circular arc centered at the vertex of the angle is drawn, e.g., with a pair of compasses. The ratio of the length s of the arc by the radius r of the circle is the number of radians in the angle:[20]
The angle expressed by another angular unit may then be obtained by multiplying the angle by a suitable conversion constant of the form k/2π, where k is the measure of a complete turn expressed in the chosen unit (for example, k = 360° for degrees or 400 grad for gradians):
The value of θ thus defined is independent of the size of the circle: if the length of the radius is changed, then the arc length changes in the same proportion, so the ratio s/r is unaltered.[nb 1]
Units
Throughout history, angles have been measured in various units. These are known as angular units, with the most contemporary units being the degree ( ° ), the radian (rad), and the gradian (grad), though many others have been used throughout history.[22] Most units of angular measurement are defined such that one turn (i.e., the angle subtended by the circumference of a circle at its centre) is equal to n units, for some whole number n. Two exceptions are the radian (and its decimal submultiples) and the diameter part.
In the International System of Quantities, an angle is defined as a dimensionless quantity, and in particular, the radian unit is dimensionless. This convention impacts how angles are treated in dimensional analysis.
The following table list some units used to represent angles.
| name | number in one turn | in degrees | description |
|---|---|---|---|
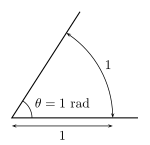
| radian | 2π | ≈57°17′ | The radian is determined by the circumference of a circle that is equal in length to the radius of the circle (n = 2π = 6.283...). It is the angle subtended by an arc of a circle that has the same length as the circle's radius. The symbol for radian is rad. One turn is 2π radians, and one radian is 180°/π, or about 57.2958 degrees. Often, particularly in mathematical texts, one radian is assumed to equal one, resulting in the unit rad being omitted. The radian is used in virtually all mathematical work beyond simple, practical geometry due, for example, to the pleasing and "natural" properties that the trigonometric functions display when their arguments are in radians. The radian is the (derived) unit of angular measurement in the SI. |
| degree | 360 | 1° | The degree, denoted by a small superscript circle (°), is 1/360 of a turn, so one turn is 360°. One advantage of this old sexagesimal subunit is that many angles common in simple geometry are measured as a whole number of degrees. Fractions of a degree may be written in normal decimal notation (e.g., 3.5° for three and a half degrees), but the "minute" and "second" sexagesimal subunits of the "degree–minute–second" system (discussed next) are also in use, especially for geographical coordinates and in astronomy and ballistics (n = 360) |
| arcminute | 21,600 | 0°1′ | The minute of arc (or MOA, arcminute, or just minute) is 1/60 of a degree = 1/21,600 turn. It is denoted by a single prime ( ′ ). For example, 3° 30′ is equal to 3 × 60 + 30 = 210 minutes or 3 + 30/60 = 3.5 degrees. A mixed format with decimal fractions is sometimes used, e.g., 3° 5.72′ = 3 + 5.72/60 degrees. A nautical mile was historically defined as an arcminute along a great circle of the Earth. (n = 21,600). |
| arcsecond | 1,296,000 | 0°0′1″ | The second of arc (or arcsecond, or just second) is 1/60 of a minute of arc and 1/3600 of a degree (n = 1,296,000). It is denoted by a double prime ( ″ ). For example, 3° 7′ 30″ is equal to 3 + 7/60 + 30/3600 degrees, or 3.125 degrees. |
| grad | 400 | 0°54′ | The grad, also called grade, gradian, or gon. It is a decimal subunit of the quadrant. A right angle is 100 grads. A kilometre was historically defined as a centi-grad of arc along a meridian of the Earth, so the kilometer is the decimal analog to the sexagesimal nautical mile (n = 400). The grad is used mostly in triangulation and continental surveying. |
| turn | 1 | 360° | The turn is the angle subtended by the circumference of a circle at its centre. A turn is equal to 2π or tau radians. |
| hour angle | 24 | 15° | The astronomical hour angle is 1/24 turn. As this system is amenable to measuring objects that cycle once per day (such as the relative position of stars), the sexagesimal subunits are called minute of time and second of time. These are distinct from, and 15 times larger than, minutes and seconds of arc. 1 hour = 15° = π/12 rad = 1/6 quad = 1/24 turn = 16+2/3 grad. |
| (compass) point | 32 | 11.25° | The point or wind, used in navigation, is 1/32 of a turn. 1 point = 1/8 of a right angle = 11.25° = 12.5 grad. Each point is subdivided into four quarter points, so one turn equals 128. |
| milliradian | 2000π | ≈0.057° | The true milliradian is defined as a thousandth of a radian, which means that a rotation of one turn would equal exactly 2000π mrad (or approximately 6283.185 mrad). Almost all scope sights for firearms are calibrated to this definition. In addition, three other related definitions are used for artillery and navigation, often called a 'mil', which are approximately equal to a milliradian. Under these three other definitions, one turn makes up for exactly 6000, 6300, or 6400 mils, spanning the range from 0.05625 to 0.06 degrees (3.375 to 3.6 minutes). In comparison, the milliradian is approximately 0.05729578 degrees (3.43775 minutes). One "NATO mil" is defined as 1/6400 of a turn. Just like with the milliradian, each of the other definitions approximates the milliradian's useful property of subtensions, i.e. that the value of one milliradian approximately equals the angle subtended by a width of 1 meter as seen from 1 km away (2π/6400 = 0.0009817... ≈ 1/1000). |
| binary degree | 256 | 1°33'45" | The binary degree, also known as the binary radian or brad or binary angular measurement (BAM).[23] The binary degree is used in computing so that an angle can be efficiently represented in a single byte (albeit to limited precision). Other measures of the angle used in computing may be based on dividing one whole turn into 2n equal parts for other values of n. |
| π radian | 2 | 180° | The multiples of π radians (MULπ) unit is implemented in the RPN scientific calculator WP 43S.[25][26][27] See also: IEEE 754 recommended operations |
| quadrant | 4 | 90° | One quadrant is a 1/4 turn and also known as a right angle. The quadrant is the unit in Euclid's Elements. In German, the symbol ∟ has been used to denote a quadrant. 1 quad = 90° = π/2 rad = 1/4 turn = 100 grad. |
| sextant | 6 | 60° | The sextant was the unit used by the Babylonians,[28][29] The degree, minute of arc and second of arc are sexagesimal subunits of the Babylonian unit. It is straightforward to construct with ruler and compasses. It is the angle of the equilateral triangle or is 1/6 turn. 1 Babylonian unit = 60° = π/3 rad ≈ 1.047197551 rad. |
| hexacontade | 60 | 6° | The hexacontade is a unit used by Eratosthenes. It equals 6°, so a whole turn was divided into 60 hexacontades. |
| pechus | 144 to 180 | 2° to 2+1/2° | The pechus was a Babylonian unit equal to about 2° or 2+1/2°. |
| diameter part | ≈376.991 | ≈0.95493° | The diameter part (occasionally used in Islamic mathematics) is 1/60 radian. One "diameter part" is approximately 0.95493°. There are about 376.991 diameter parts per turn. |
| zam | 224 | ≈1.607° | In old Arabia, a turn was subdivided into 32 Akhnam, and each akhnam was subdivided into 7 zam so that a turn is 224 zam. |
Dimensional analysis
Plane angle may be defined as θ = s/r, where θ is the subtended angle in radians, s is arc length, and r is radius. One radian corresponds to the angle for which s = r, hence 1 radian = 1 m/m.[30] However, rad is only to be used to express angles, not to express ratios of lengths in general.[31] A similar calculation using the area of a circular sector θ = 2A/r2 gives 1 radian as 1 m2/m2.[32] The key fact is that the radian is a dimensionless unit equal to 1. In SI 2019, the radian is defined accordingly as 1 rad = 1.[33] It is a long-established practice in mathematics and across all areas of science to make use of rad = 1.[34][35]
Giacomo Prando writes "the current state of affairs leads inevitably to ghostly appearances and disappearances of the radian in the dimensional analysis of physical equations".[36] For example, an object hanging by a string from a pulley will rise or drop by y = rθ centimeters, where r is the radius of the pulley in centimeters and θ is the angle the pulley turns in radians. When multiplying r by θ the unit of radians disappears from the result. Similarly in the formula for the angular velocity of a rolling wheel, ω = v/r, radians appear in the units of ω but not on the right hand side.[37] Anthony French calls this phenomenon "a perennial problem in the teaching of mechanics".[38] Oberhofer says that the typical advice of ignoring radians during dimensional analysis and adding or removing radians in units according to convention and contextual knowledge is "pedagogically unsatisfying".[39]
In 1993 the American Association of Physics Teachers Metric Committee specified that the radian should explicitly appear in quantities only when different numerical values would be obtained when other angle measures were used, such as in the quantities of angle measure (rad), angular speed (rad/s), angular acceleration (rad/s2), and torsional stiffness (N⋅m/rad), and not in the quantities of torque (N⋅m) and angular momentum (kg⋅m2/s).[40]
At least a dozen scientists between 1936 and 2022 have made proposals to treat the radian as a base unit of measurement for a base quantity (and dimension) of "plane angle".[41][42][43] Quincey's review of proposals outlines two classes of proposal. The first option changes the unit of a radius to meters per radian, but this is incompatible with dimensional analysis for the area of a circle, πr2. The other option is to introduce a dimensional constant. According to Quincey this approach is "logically rigorous" compared to SI, but requires "the modification of many familiar mathematical and physical equations".[44] A dimensional constant for angle is "rather strange" and the difficulty of modifying equations to add the dimensional constant is likely to preclude widespread use.[43]
In particular, Quincey identifies Torrens' proposal to introduce a constant η equal to 1 inverse radian (1 rad−1) in a fashion similar to the introduction of the constant ε0.[44][a] With this change the formula for the angle subtended at the center of a circle, s = rθ, is modified to become s = ηrθ, and the Taylor series for the sine of an angle θ becomes:[43][45]
Current SI can be considered relative to this framework as a natural unit system where the equation η = 1 is assumed to hold, or similarly, 1 rad = 1. This radian convention allows the omission of η in mathematical formulas.[48]
Defining radian as a base unit may be useful for software, where the disadvantage of longer equations is minimal.[49] For example, the Boost units library defines angle units with aplane_angle dimension,[50] and Mathematica's unit system similarly considers angles to have an angle dimension.[51][52]Signed angles

It is frequently helpful to impose a convention that allows positive and negative angular values to represent orientations and/or rotations in opposite directions or "sense" relative to some reference.
In a two-dimensional Cartesian coordinate system, an angle is typically defined by its two sides, with its vertex at the origin. The initial side is on the positive x-axis, while the other side or terminal side is defined by the measure from the initial side in radians, degrees, or turns, with positive angles representing rotations toward the positive y-axis and negative angles representing rotations toward the negative y-axis. When Cartesian coordinates are represented by standard position, defined by the x-axis rightward and the y-axis upward, positive rotations are anticlockwise, and negative cycles are clockwise.
In many contexts, an angle of −θ is effectively equivalent to an angle of "one full turn minus θ". For example, an orientation represented as −45° is effectively equal to an orientation defined as 360° − 45° or 315°. Although the final position is the same, a physical rotation (movement) of −45° is not the same as a rotation of 315° (for example, the rotation of a person holding a broom resting on a dusty floor would leave visually different traces of swept regions on the floor).
In three-dimensional geometry, "clockwise" and "anticlockwise" have no absolute meaning, so the direction of positive and negative angles must be defined in terms of an orientation, which is typically determined by a normal vector passing through the angle's vertex and perpendicular to the plane in which the rays of the angle lie.
In navigation, bearings or azimuth are measured relative to north. By convention, viewed from above, bearing angles are positive clockwise, so a bearing of 45° corresponds to a north-east orientation. Negative bearings are not used in navigation, so a north-west orientation corresponds to a bearing of 315°.
Equivalent angles
- Angles that have the same measure (i.e., the same magnitude) are said to be equal or congruent. An angle is defined by its measure and is not dependent upon the lengths of the sides of the angle (e.g., all right angles are equal in measure).
- Two angles that share terminal sides, but differ in size by an integer multiple of a turn, are called coterminal angles.
- The reference angle (sometimes called related angle) for any angle θ in standard position is the positive acute angle between the terminal side of θ and the x-axis (positive or negative).[53][54] Procedurally, the magnitude of the reference angle for a given angle may determined by taking the angle's magnitude modulo 1/2 turn, 180°, or π radians, then stopping if the angle is acute, otherwise taking the supplementary angle, 180° minus the reduced magnitude. For example, an angle of 30 degrees is already a reference angle, and an angle of 150 degrees also has a reference angle of 30 degrees (180° − 150°). Angles of 210° and 510° correspond to a reference angle of 30 degrees as well (210° mod 180° = 30°, 510° mod 180° = 150° whose supplementary angle is 30°).
Related quantities
For an angular unit, it is definitional that the angle addition postulate holds. Some quantities related to angles where the angle addition postulate does not hold include:
- The slope or gradient is equal to the tangent of the angle; a gradient is often expressed as a percentage. For very small values (less than 5%), the slope of a line is approximately the measure in radians of its angle with the horizontal direction.
- The spread between two lines is defined in rational geometry as the square of the sine of the angle between the lines. As the sine of an angle and the sine of its supplementary angle are the same, any angle of rotation that maps one of the lines into the other leads to the same value for the spread between the lines.
- Although done rarely, one can report the direct results of trigonometric functions, such as the sine of the angle.
Angles between curves

The angle between a line and a curve (mixed angle) or between two intersecting curves (curvilinear angle) is defined to be the angle between the tangents at the point of intersection. Various names (now rarely, if ever, used) have been given to particular cases:—amphicyrtic (Gr. ἀμφί, on both sides, κυρτός, convex) or cissoidal (Gr. κισσός, ivy), biconvex; xystroidal or sistroidal (Gr. ξυστρίς, a tool for scraping), concavo-convex; amphicoelic (Gr. κοίλη, a hollow) or angulus lunularis, biconcave.[55]
Bisecting and trisecting angles
The ancient Greek mathematicians knew how to bisect an angle (divide it into two angles of equal measure) using only a compass and straightedge but could only trisect certain angles. In 1837, Pierre Wantzel showed that this construction could not be performed for most angles.
Dot product and generalisations
In the Euclidean space, the angle θ between two Euclidean vectors u and v is related to their dot product and their lengths by the formula
This formula supplies an easy method to find the angle between two planes (or curved surfaces) from their normal vectors and between skew lines from their vector equations.
Inner product
To define angles in an abstract real inner product space, we replace the Euclidean dot product ( · ) by the inner product , i.e.
In a complex inner product space, the expression for the cosine above may give non-real values, so it is replaced with
or, more commonly, using the absolute value, with
The latter definition ignores the direction of the vectors. It thus describes the angle between one-dimensional subspaces and spanned by the vectors and correspondingly.
Angles between subspaces
The definition of the angle between one-dimensional subspaces and given by
in a Hilbert space can be extended to subspaces of finite dimensions. Given two subspaces , with , this leads to a definition of angles called canonical or principal angles between subspaces.
Angles in Riemannian geometry
In Riemannian geometry, the metric tensor is used to define the angle between two tangents. Where U and V are tangent vectors and gij are the components of the metric tensor G,
Hyperbolic angle
A hyperbolic angle is an argument of a hyperbolic function just as the circular angle is the argument of a circular function. The comparison can be visualized as the size of the openings of a hyperbolic sector and a circular sector since the areas of these sectors correspond to the angle magnitudes in each case. Unlike the circular angle, the hyperbolic angle is unbounded. When the circular and hyperbolic functions are viewed as infinite series in their angle argument, the circular ones are just alternating series forms of the hyperbolic functions. This weaving of the two types of angle and function was explained by Leonhard Euler in Introduction to the Analysis of the Infinite.
Angles in geography and astronomy
In geography, the location of any point on the Earth can be identified using a geographic coordinate system. This system specifies the latitude and longitude of any location in terms of angles subtended at the center of the Earth, using the equator and (usually) the Greenwich meridian as references.
In astronomy, a given point on the celestial sphere (that is, the apparent position of an astronomical object) can be identified using any of several astronomical coordinate systems, where the references vary according to the particular system. Astronomers measure the angular separation of two stars by imagining two lines through the center of the Earth, each intersecting one of the stars. The angle between those lines and the angular separation between the two stars can be measured.
In both geography and astronomy, a sighting direction can be specified in terms of a vertical angle such as altitude /elevation with respect to the horizon as well as the azimuth with respect to north.
Astronomers also measure objects' apparent size as an angular diameter. For example, the full moon has an angular diameter of approximately 0.5° when viewed from Earth. One could say, "The Moon's diameter subtends an angle of half a degree." The small-angle formula can convert such an angular measurement into a distance/size ratio.
Other astronomical approximations include:
- 0.5° is the approximate diameter of the Sun and of the Moon as viewed from Earth.
- 1° is the approximate width of the little finger at arm's length.
- 10° is the approximate width of a closed fist at arm's length.
- 20° is the approximate width of a handspan at arm's length.
These measurements depend on the individual subject, and the above should be treated as rough rule of thumb approximations only.
In astronomy, right ascension and declination are usually measured in angular units, expressed in terms of time, based on a 24-hour day.
| Unit | Symbol | Degrees | Radians | Turns | Other |
|---|---|---|---|---|---|
| Hour | h | 15° | π⁄12 rad | 1⁄24 turn | |
| Minute | m | 0°15′ | π⁄720 rad | 1⁄1,440 turn | 1⁄60 hour |
| Second | s | 0°0′15″ | π⁄43200 rad | 1⁄86,400 turn | 1⁄60 minute |
See also
- Angle measuring instrument
- Angles between flats
- Angular statistics (mean, standard deviation)
- Angle bisector
- Angular acceleration
- Angular diameter
- Angular velocity
- Argument (complex analysis)
- Astrological aspect
- Central angle
- Clock angle problem
- Decimal degrees
- Dihedral angle
- Exterior angle theorem
- Golden angle
- Great circle distance
- Horn angle
- Inscribed angle
- Irrational angle
- Phase (waves)
- Protractor
- Solid angle
- Spherical angle
- Transcendent angle
- Trisection
- Zenith angle
Notes
- ^ This approach requires, however, an additional proof that the measure of the angle does not change with changing radius r, in addition to the issue of "measurement units chosen". A smoother approach is to measure the angle by the length of the corresponding unit circle arc. Here "unit" can be chosen to be dimensionless in the sense that it is the real number 1 associated with the unit segment on the real line. See Radoslav M. Dimitrić, for instance.[21]
- ^ Other proposals include the abbreviation "rad" (Brinsmade 1936), the notation (Romain 1962), and the constants ם (Brownstein 1997), ◁ (Lévy-Leblond 1998), k (Foster 2010), θC (Quincey 2021), and (Mohr et al. 2022).
References
- ^ Sidorov 2001
- ^ Slocum 2007
- ^ Chisholm 1911; Heiberg 1908, pp. 177–178
- ^ Aboughantous 2010, p. 18.
- ^ a b Moser 1971, p. 41.
- ^ a b Godfrey & Siddons 1919, p. 9.
- ^ Moser 1971, p. 71.
- ^ Wong & Wong 2009, pp. 161–163
- ^ Euclid. The Elements. Proposition I:13.
- ^ a b Shute, Shirk & Porter 1960, pp. 25–27.
- ^ Jacobs 1974, p. 255.
- ^ "Complementary Angles". www.mathsisfun.com. Retrieved 2020-08-17.
- ^ a b Chisholm 1911
- ^ "Supplementary Angles". www.mathsisfun.com. Retrieved 2020-08-17.
- ^ Jacobs 1974, p. 97.
- ^ Willis, Clarence Addison (1922). Plane Geometry. Blakiston's Son. p. 8.
- ^ Henderson & Taimina 2005, p. 104.
- ^ a b c Johnson, Roger A. Advanced Euclidean Geometry, Dover Publications, 2007.
- ^ D. Zwillinger, ed. (1995), CRC Standard Mathematical Tables and Formulae, Boca Raton, FL: CRC Press, p. 270 as cited in Weisstein, Eric W. "Exterior Angle". MathWorld.
- ^ International Bureau of Weights and Measures (20 May 2019), The International System of Units (SI) (PDF) (9th ed.), ISBN 978-92-822-2272-0, archived from the original on 18 October 2021
- ^ Dimitrić, Radoslav M. (2012). "On Angles and Angle Measurements" (PDF). The Teaching of Mathematics. XV (2): 133–140. Archived (PDF) from the original on 2019-01-17. Retrieved 2019-08-06.
- ^ "angular unit". TheFreeDictionary.com. Retrieved 2020-08-31.
- ^ a b "ooPIC Programmer's Guide - Chapter 15: URCP". ooPIC Manual & Technical Specifications - ooPIC Compiler Ver 6.0. Savage Innovations, LLC. 2007 [1997]. Archived from the original on 2008-06-28. Retrieved 2019-08-05.
- ^ Hargreaves, Shawn [in Polish]. "Angles, integers, and modulo arithmetic". blogs.msdn.com. Archived from the original on 2019-06-30. Retrieved 2019-08-05.
- ^ Bonin, Walter (2016-01-11). "RE: WP-32S in 2016?". HP Museum. Archived from the original on 2019-08-06. Retrieved 2019-08-05.
- ^ Bonin, Walter (2019) [2015]. WP 43S Owner's Manual (PDF). 0.12 (draft ed.). pp. 72, 118–119, 311. ISBN 978-1-72950098-9. Retrieved 2019-08-05.[permanent dead link] [1] [2] (314 pages)
- ^ Bonin, Walter (2019) [2015]. WP 43S Reference Manual (PDF). 0.12 (draft ed.). pp. iii, 54, 97, 128, 144, 193, 195. ISBN 978-1-72950106-1. Retrieved 2019-08-05.[permanent dead link] [3] [4] (271 pages)
- ^ Jeans, James Hopwood (1947). The Growth of Physical Science. CUP Archive. p. 7.
- ^ Murnaghan, Francis Dominic (1946). Analytic Geometry. p. 2.
- ^ International Bureau of Weights and Measures 2019, p. 151: "One radian corresponds to the angle for which s = r"
- ^ International Bureau of Weights and Measures 2019, p. 151.
- ^ Quincey 2016, p. 844: "Also, as alluded to in Mohr & Phillips 2015, the radian can be defined in terms of the area A of a sector (A = 1/2 θ r2), in which case it has the units m2⋅m−2."
- ^ International Bureau of Weights and Measures 2019, p. 151: "One radian corresponds to the angle for which s = r, thus 1 rad = 1."
- ^ International Bureau of Weights and Measures 2019, p. 137.
- ^ Bridgman, Percy Williams (1922). Dimensional analysis. New Haven : Yale University Press.
Angular amplitude of swing [...] No dimensions.
- ^ Prando, Giacomo (August 2020). "A spectral unit". Nature Physics. 16 (8): 888. Bibcode:2020NatPh..16..888P. doi:10.1038/s41567-020-0997-3. S2CID 225445454.
- ^ Leonard, William J. (1999). Minds-on Physics: Advanced topics in mechanics. Kendall Hunt. p. 262. ISBN 978-0-7872-5412-4.
- ^ French, Anthony P. (May 1992). "What happens to the 'radians'? (comment)". The Physics Teacher. 30 (5): 260–261. doi:10.1119/1.2343535.
- ^ Oberhofer, E. S. (March 1992). "What happens to the 'radians'?". The Physics Teacher. 30 (3): 170–171. Bibcode:1992PhTea..30..170O. doi:10.1119/1.2343500.
- ^ Aubrecht, Gordon J.; French, Anthony P.; Iona, Mario; Welch, Daniel W. (February 1993). "The radian—That troublesome unit". The Physics Teacher. 31 (2): 84–87. Bibcode:1993PhTea..31...84A. doi:10.1119/1.2343667.
- ^ Brinsmade 1936; Romain 1962; Eder 1982; Torrens 1986; Brownstein 1997; Lévy-Leblond 1998; Foster 2010; Mills 2016; Quincey 2021; Leonard 2021; Mohr et al. 2022
- ^ Mohr & Phillips 2015.
- ^ a b c d Quincey, Paul; Brown, Richard J C (1 June 2016). "Implications of adopting plane angle as a base quantity in the SI". Metrologia. 53 (3): 998–1002. arXiv:1604.02373. Bibcode:2016Metro..53..998Q. doi:10.1088/0026-1394/53/3/998. S2CID 119294905.
- ^ a b Quincey 2016.
- ^ a b Torrens 1986.
- ^ Mohr et al. 2022, p. 6.
- ^ Mohr et al. 2022, pp. 8–9.
- ^ Quincey 2021.
- ^ Quincey, Paul; Brown, Richard J C (1 August 2017). "A clearer approach for defining unit systems". Metrologia. 54 (4): 454–460. arXiv:1705.03765. Bibcode:2017Metro..54..454Q. doi:10.1088/1681-7575/aa7160. S2CID 119418270.
- ^ Schabel, Matthias C.; Watanabe, Steven. "Boost.Units FAQ – 1.79.0". www.boost.org. Retrieved 5 May 2022.
Angles are treated as units
- ^ Mohr et al. 2022, p. 3.
- ^ "UnityDimensions—Wolfram Language Documentation". reference.wolfram.com. Retrieved 1 July 2022.
- ^ "Mathwords: Reference Angle". www.mathwords.com. Archived from the original on 23 October 2017. Retrieved 26 April 2018.
- ^ McKeague, Charles P. (2008). Trigonometry (6th ed.). Belmont, CA: Thomson Brooks/Cole. p. 110. ISBN 978-0495382607.
- ^ Chisholm 1911; Heiberg 1908, p. 178
Bibliography
- Aboughantous, Charles H. (2010), A High School First Course in Euclidean Plane Geometry, Universal Publishers, ISBN 978-1-59942-822-2
- Brinsmade, J. B. (December 1936). "Plane and Solid Angles. Their Pedagogic Value When Introduced Explicitly". American Journal of Physics. 4 (4): 175–179. Bibcode:1936AmJPh...4..175B. doi:10.1119/1.1999110.
- Brownstein, K. R. (July 1997). "Angles—Let's treat them squarely". American Journal of Physics. 65 (7): 605–614. Bibcode:1997AmJPh..65..605B. doi:10.1119/1.18616.
- Eder, W E (January 1982). "A Viewpoint on the Quantity "Plane Angle"". Metrologia. 18 (1): 1–12. Bibcode:1982Metro..18....1E. doi:10.1088/0026-1394/18/1/002. S2CID 250750831.
- Foster, Marcus P (1 December 2010). "The next 50 years of the SI: a review of the opportunities for the e-Science age". Metrologia. 47 (6): R41–R51. doi:10.1088/0026-1394/47/6/R01. S2CID 117711734.
- Godfrey, Charles; Siddons, A. W. (1919), Elementary geometry: practical and theoretical (3rd ed.), Cambridge University Press
- Henderson, David W.; Taimina, Daina (2005), Experiencing Geometry / Euclidean and Non-Euclidean with History (3rd ed.), Pearson Prentice Hall, p. 104, ISBN 978-0-13-143748-7
- Heiberg, Johan Ludvig (1908), Heath, T. L. (ed.), Euclid, The Thirteen Books of Euclid's Elements, vol. 1, Cambridge: Cambridge University Press.
- Jacobs, Harold R. (1974), Geometry, W. H. Freeman, pp. 97, 255, ISBN 978-0-7167-0456-0
- Leonard, B P (1 October 2021). "Proposal for the dimensionally consistent treatment of angle and solid angle by the International System of Units (SI)". Metrologia. 58 (5): 052001. Bibcode:2021Metro..58e2001L. doi:10.1088/1681-7575/abe0fc. S2CID 234036217.
- Lévy-Leblond, Jean-Marc (September 1998). "Dimensional angles and universal constants". American Journal of Physics. 66 (9): 814–815. Bibcode:1998AmJPh..66..814L. doi:10.1119/1.18964.
- Mills, Ian (1 June 2016). "On the units radian and cycle for the quantity plane angle". Metrologia. 53 (3): 991–997. Bibcode:2016Metro..53..991M. doi:10.1088/0026-1394/53/3/991. S2CID 126032642.
- Mohr, Peter J; Phillips, William D (1 February 2015). "Dimensionless units in the SI". Metrologia. 52 (1): 40–47. arXiv:1409.2794. Bibcode:2015Metro..52...40M. doi:10.1088/0026-1394/52/1/40.
- Mohr, Peter J; Shirley, Eric L; Phillips, William D; Trott, Michael (23 June 2022). "On the dimension of angles and their units". Metrologia. 59 (5): 053001. arXiv:2203.12392. Bibcode:2022Metro..59e3001M. doi:10.1088/1681-7575/ac7bc2.
- Moser, James M. (1971), Modern Elementary Geometry, Prentice-Hall
- Quincey, Paul (1 April 2016). "The range of options for handling plane angle and solid angle within a system of units". Metrologia. 53 (2): 840–845. Bibcode:2016Metro..53..840Q. doi:10.1088/0026-1394/53/2/840. S2CID 125438811.
- Quincey, Paul (1 October 2021). "Angles in the SI: a detailed proposal for solving the problem". Metrologia. 58 (5): 053002. arXiv:2108.05704. Bibcode:2021Metro..58e3002Q. doi:10.1088/1681-7575/ac023f. S2CID 236547235.
- Romain, Jacques E. (July 1962). "Angle as a fourth fundamental quantity". Journal of Research of the National Bureau of Standards Section B. 66B (3): 97. doi:10.6028/jres.066B.012.
- Sidorov, L. A. (2001) [1994], "Angle", Encyclopedia of Mathematics, EMS Press
- Slocum, Jonathan (2007), Preliminary Indo-European lexicon — Pokorny PIE data, University of Texas research department: linguistics research center, archived from the original on 27 June 2010, retrieved 2 Feb 2010
- Shute, William G.; Shirk, William W.; Porter, George F. (1960), Plane and Solid Geometry, American Book Company, pp. 25–27
- Torrens, A B (1 January 1986). "On Angles and Angular Quantities". Metrologia. 22 (1): 1–7. Bibcode:1986Metro..22....1T. doi:10.1088/0026-1394/22/1/002. S2CID 250801509.
- Wong, Tak-wah; Wong, Ming-sim (2009), "Angles in Intersecting and Parallel Lines", New Century Mathematics, vol. 1B (1 ed.), Hong Kong: Oxford University Press, pp. 161–163, ISBN 978-0-19-800177-5
This article incorporates text from a publication now in the public domain: Chisholm, Hugh, ed. (1911), "Angle", Encyclopædia Britannica, vol. 2 (11th ed.), Cambridge University Press, p. 14
External links
- , Encyclopædia Britannica, vol. 2 (9th ed.), 1878, pp. 29–30



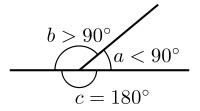


![{\displaystyle {\begin{aligned}&\sin ^{2}A+\sin ^{2}B=1&&\cos ^{2}A+\cos ^{2}B=1\\[3pt]&\tan A=\cot B&&\sec A=\csc B\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47aa6b35b8e53468f73d7ec051d55371da314fba)