A population model is a type of mathematical model that is applied to the study of population dynamics.
YouTube Encyclopedic
-
1/5Views:177 66715 94614 15152634 038
-
Modeling population with simple differential equation | Khan Academy
-
Population Modeling
-
ODE | Population models
-
Single species population model - stability and bifurcation
-
Population Growth Model
Transcription
- What I'd like to do in this video is start exploring how we can model things with the differential equations. And in this video in particular, we will explore modeling population. Modeling population. We're actually going to go into some depth on this eventually, but here we're going to start with simpler models. And we'll see, we will stumble on using the logic of differential equations. Things that you might have seen in your algebra or your precalculus class. So, in some level, what we're going to do here is going to be review, but we're going to get there using the power of modeling with differential equations. So let's just define some variables. Let's say that P is equal to our population. And let's say that t is, let's say that t is equal to the time that has passed in days. In days, it could have been years or months. But let's say we're doing the population of insects that reproduce quite quickly. So days seem like a nice time span to care about. Now, what would be a reasonable model? Well, we could say that the rate of change, the rate of change of our population, with respect to time, with respect to time is, well, a reasonable thing to say is that it's going to be proportional to the actual population, the actual population. Why is that reasonable? Well, the larger the population, the larger the rate at any given time. If you have a thousand people, the rate at which they're reproducing is going to be more, or a thousand insects is going to be more insects per second, per day or per year than if you only have 10 insects. So it makes sense that the rate of growth of your population, with respect to time, is going to be proportional to your population. And so, you know, sometimes you think of differential equations as these daunting complex things, but notice we've just been able to express a reasonably not so complicated idea. The rate of change of population is going to be proportional to the population. And now, once we've expressed that, we can actually try to solve this differential equation. Find a general solution, and then we can try to put some initial conditions on there or some states of the population that we know to actually solve for the constants to find a particular solution. So how do we do that? And I encourage you to pause the video at any time and see if you can solve this differential equation. So assuming you, at least, maybe have had an attempt at it, and you might immediately recognize that this is a separable differential equation. And in separable differential equations, we want one variable and all the differentials involving that variable on one side, and the other variable and all the differentials involving the other variable on the other side, and then we can integrate both sides. And once again, dP, the derivative of P with respect to t, this isn't quite a fraction. This is the limit as our change in P over change in time. This is our instantaneous change, but for the sake of separable differential equations or differential equations in general, you can treat, you can treat these, this derivative in Leibniz notations like fractions, and you can treat these differentials like quantities because we will eventually integrate them. So let's do that. So, we want to put all the Ps and dPs on one side and all the, all the things that involve t or that I guess don't involve P on the other side. So, we could divide both sides by P. We could divide both sides by P, and so we'll have one over P, and you have one over P here and then those will cancel, and then you can multiply both sides times dt. We could multiply both sides times dt. Once again, treating the differential like a quantity which isn't, it really isn't a quantity. You really have to view this as a limit of change in P over change in time. The limit as we get smaller and smaller and smaller changes in time. But for, once again, for the sake of this we can do this, and when we do that we would be left with one over P dP is equal to, is equal to k dt, is equal to k dt. Now we can integrate, integrate both sides. Because this was a separable differential equation, we were able to completely separate the Ps and dPs from the things involving ts or, I guess, the things that aren't involving Ps, and then if we integrate this side, we would get the natural log, the natural log of the absolute value of our population, and we could say plus some constant if we want but we're going to get a constant on this side as well so we could just say that's going to be equal to, that's going to be equal to k, it's going to be equal to k times t, k times t plus some constant. Plus some constant. I'll just call that C one, and once again I could've put a plus C two here, but I could've then subtracted the constant from both sides and I would just get the constant on the right hand side. Now, how can I solve for P? Well, the natural log of the absolute value of P is equal to this thing right over here. That means that's the same thing. That means that the absolute value of P, that means that the absolute value of P is equal to e to all this business, e to the, e to the, let me do in the same colors, kt, kt plus, plus C one, plus C one. Now this right over here is the same thing. Just using our exponent properties, this is the same thing as e to the kt, e to the k times t times e, times e to the C one, e to the C one. Now this is just e to some constant, so we could just call this, let's just call that the constant C. So this is all simplified to C e, C e to the kt, to the kt. And if we assume our population at any given time is positive then we could get rid of this absolute value sign, and we have a general solution to this, frankly, fairly general differential equation. We just said proportional. We haven't given what the proportionality constant is, but we could say, if we assume, positive population that the population is going to be equal to some constant C times e to the kt power. To the kt power, and the reason why I said that you've seen this before is this is just an exponential function, and it's very likely that in algebra or in precalculus class you have modeled things with exponential functions, and my guess is that you've modeled things, modeled things like population. The reason why this is interesting is you now see where this is coming from. The underlying logic that's just driven by the actual differential equation. The rate of change, with respect to time, of the population. Well, maybe it's just proportional to population. So I'll leave you there, and in the next video we'll do what you probably did in the 10th or 11th grade or maybe later in your life, it doesn't matter when you did it, where we actually look at some initial conditions to find a particular solution.
Rationale
Models allow a better understanding of how complex interactions and processes work. Modeling of dynamic interactions in nature can provide a manageable way of understanding how numbers change over time or in relation to each other. Many patterns can be noticed by using population modeling as a tool.[1]
Ecological population modeling is concerned with the changes in parameters such as population size and age distribution within a population. This might be due to interactions with the environment, individuals of their own species, or other species.[2]
Population models are used to determine maximum harvest for agriculturists, to understand the dynamics of biological invasions, and for environmental conservation. Population models are also used to understand the spread of parasites, viruses, and disease.[2]
Another way populations models are useful are when species become endangered. Population models can track the fragile species and work and curb the decline. [1]
History
Late 18th-century biologists began to develop techniques in population modeling in order to understand the dynamics of growing and shrinking of all populations of living organisms. Thomas Malthus was one of the first to note that populations grew with a geometric pattern while contemplating the fate of humankind.[3] One of the most basic and milestone models of population growth was the logistic model of population growth formulated by Pierre François Verhulst in 1838. The logistic model takes the shape of a sigmoid curve and describes the growth of a population as exponential, followed by a decrease in growth, and bound by a carrying capacity due to environmental pressures.[4]
Population modeling became of particular interest to biologists in the 20th century as pressure on limited means of sustenance due to increasing human populations in parts of Europe were noticed by biologist like Raymond Pearl. In 1921 Pearl invited physicist Alfred J. Lotka to assist him in his lab. Lotka developed paired differential equations that showed the effect of a parasite on its prey. Mathematician Vito Volterra equated the relationship between two species independent from Lotka. Together, Lotka and Volterra formed the Lotka–Volterra model for competition that applies the logistic equation to two species illustrating competition, predation, and parasitism interactions between species.[3] In 1939 contributions to population modeling were given by Patrick Leslie as he began work in biomathematics. Leslie emphasized the importance of constructing a life table in order to understand the effect that key life history strategies played in the dynamics of whole populations. Matrix algebra was used by Leslie in conjunction with life tables to extend the work of Lotka.[5] Matrix models of populations calculate the growth of a population with life history variables. Later, Robert MacArthur and E. O. Wilson characterized island biogeography. The equilibrium model of island biogeography describes the number of species on an island as an equilibrium of immigration and extinction. The logistic population model, the Lotka–Volterra model of community ecology, life table matrix modeling, the equilibrium model of island biogeography and variations thereof are the basis for ecological population modeling today.[6]
Equations
Logistic growth equation:
Competitive Lotka–Volterra equations:
Examples of individual-based models

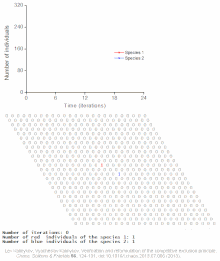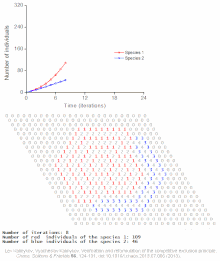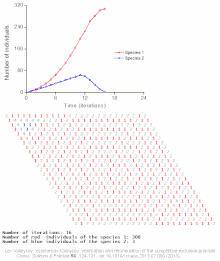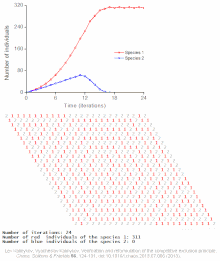
See also
References
- ^ Worster, Donald (1994). Nature's Economy. Cambridge University Press. pp. 398–401.
- ^ a b Uyenoyama, Marcy (2004). Rama Singh (ed.). The Evolution of Population Biology. Cambridge University Press. pp. 1–19.
- ^ a b McIntosh, Robert (1985). The Background of Ecology. Cambridge University Press. pp. 171–198.
- ^ Renshaw, Eric (1991). Modeling Biological Populations in Space and Time. Cambridge University Press. pp. 6–9.
- ^ Kingsland, Sharon (1995). Modeling Nature: Episodes in the History of Population Ecology. University of Chicago Press. pp. 127–146.
- ^ Gotelli, Nicholas (2001). A Primer of Ecology. Sinauer.
External links
- GreenBoxes code sharing network. Greenboxes (Beta) is a repository for open-source population modeling code. Greenboxes allows users an easy way to share their code and to search for others shared code.




