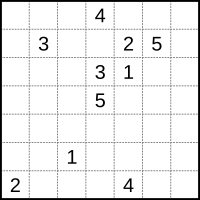
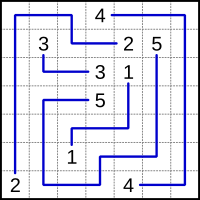
Numberlink is a type of logic puzzle involving finding paths to connect numbers in a grid.
YouTube Encyclopedic
-
1/3Views:387133 97530 672
-
Aadhar card se mobile number link
-
How To Link Aadhar Card With Mobile number | आधार कार्ड से लिंक करने की आखिरी तारीख और सही तरीका
-
How to Link Aadhar Card with Mobile Number | Jio, Airtel, BSNL - Tamil
Transcription
Rules
The player has to pair up all the matching numbers on the grid with single continuous lines (or paths). The lines cannot branch off or cross over each other, and the numbers have to fall at the end of each line (i.e., not in the middle).
It is considered that a problem is well-designed only if it has a unique solution[1] and all the cells in the grid are filled, although some Numberlink designers do not stipulate this.
History
In 1897, a slightly different form of the puzzle was printed in the Brooklyn Daily Eagle, in a column by Sam Loyd.[2] Another early, printed version of Number Link can be found in Henry Ernest Dudeney's book Amusements in mathematics (1917) as a puzzle for motorists (puzzle no. 252).[3] This puzzle type was popularized in Japan by Nikoli as Arukone (アルコネ, Alphabet Connection) and Nanbarinku (ナンバーリンク, Number Link). The only difference between Arukone and Nanbarinku is that in Arukone the clues are letter pairs (as in Dudeney's puzzle), while in Nanbarinku the clues are number pairs.
As of 2006[update], three books consisting entirely of Numberlink puzzles have been published by Nikoli.
Versions of this known as Wire Storm, Flow Free and Alphabet Connection have been released as apps for iOS, Android and Windows Phone.[4][5][6][7][8][9]
Computational complexity
As a computational problem, finding a solution to a given Numberlink puzzle is NP-complete.[10] NP-completeness is maintained even if "zig-zag" paths are allowed. Informally, this means paths may have "unnecessary bends" in them (see the reference for a more technical explanation).[11]
See also
References
- ^ Thomas Snyder (19 November 2010). "Dr. Sudoku Prescribes: Numberlink Puzzles". Wired. Retrieved November 23, 2010.
- ^ Pegg Jr., Ed (2007). "Beyond Sudoku" (PDF). Mathematica Journal. 10 (3): 469–73. Archived from the original (PDF) on 3 March 2016. Retrieved 11 September 2011.
- ^ Dudeney, Henry (1917). "Problem 252 – A Puzzle for Motorists". Amusements in mathematics. Thomas Nelson.
- ^ "Wire Storm - Fun and Addicting Logic Flow Puzzle Game for bigst4t22,…". Archive.today. 20 June 2013. Archived from the original on 20 June 2013. Retrieved 22 November 2018.
- ^ "Flow Free". App Store. Retrieved 22 November 2018.
- ^ "Flow Free - Apps on Google Play". Play.google.com. Retrieved 22 November 2018.
- ^ "Alphabet Connection: Arukone on the App Store on iTunes". iTunes. Archived from the original on 2015-03-22. Retrieved 2015-03-17.
- ^ "Archived copy". Archived from the original on 2015-04-07. Retrieved 2013-10-29.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ "Get Flow Free - Microsoft Store en-GB". Microsoft Store. Retrieved 22 November 2018.
- ^ Kotsuma, Kouichi; Takenaga, Yasuhiko (March 2010), "NP-Completeness and Enumeration of Number Link Puzzle", IEICE Technical Report. Theoretical Foundations of Computing, 109 (465): 1–7
- ^ Adcock, Aaron; Demaine, Erik D.; Demaine, Martin L; O’Brien, Michael P.; Villaamil, Fernando S{\'a}nchez; D. Sullivan, Blair (October 23, 2014), "Zig-Zag Numberlink is NP-Complete", Journal of Information Processing, 23 (3): 239–245, arXiv:1410.5845, doi:10.2197/ipsjjip.23.239, S2CID 15735280
External links
This page was last edited on 12 December 2023, at 08:50