Binary expression tree

A binary expression tree is a specific kind of a binary tree used to represent expressions. Two common types of expressions that a binary expression tree can represent are algebraic^[1] and boolean. These trees can represent expressions that contain both unary and binary operators.^[1]

Like any binary tree, each node of a binary expression tree has zero, one, or two children. This restricted structure simplifies the processing of expression trees.

YouTube Encyclopedic

1/3
Views:
208 253
102 835
8 404

Transcription

Construction of an expression tree

Example

The input in postfix notation is: a b + c d e + * * Since the first two symbols are operands, one-node trees are created and pointers to them are pushed onto a stack. For convenience the stack will grow from left to right.

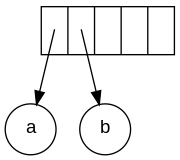
The next symbol is a '+'. It pops the two pointers to the trees, a new tree is formed, and a pointer to it is pushed onto the stack.

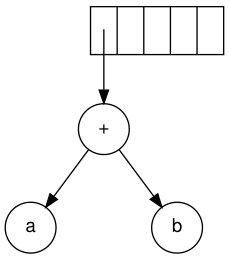
Next, c, d, and e are read. A one-node tree is created for each and a pointer to the corresponding tree is pushed onto the stack.

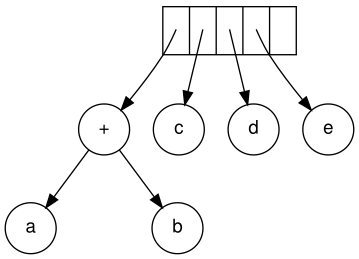
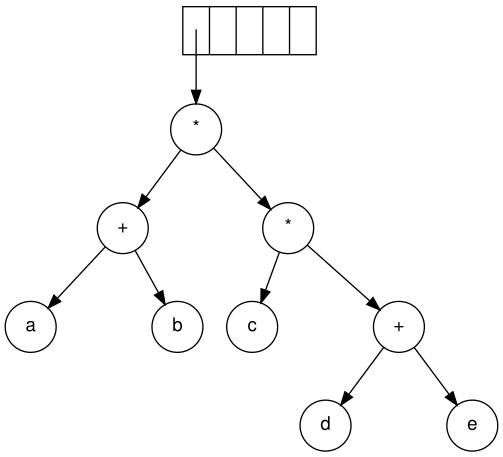
Continuing, a '+' is read, and it merges the last two trees.

Now, a '*' is read. The last two tree pointers are popped and a new tree is formed with a '*' as the root.

Finally, the last symbol is read. The two trees are merged and a pointer to the final tree remains on the stack.^[2]

Steps to construct an expression tree a b + c d e + * *

Algebraic expressions

Binary algebraic expression tree equivalent to ((5 + z) / -8) * (4 ^ 2)

Algebraic expression trees represent expressions that contain numbers, variables, and unary and binary operators. Some of the common operators are × (multiplication), ÷ (division), + (addition), − (subtraction), ^ (exponentiation), and - (negation). The operators are contained in the internal nodes of the tree, with the numbers and variables in the leaf nodes.^[1] The nodes of binary operators have two child nodes, and the unary operators have one child node.

Boolean expressions

Binary boolean expression tree equivalent to ((true $\lor$ false) $\land$ $\neg$ false) $\lor$ (true $\lor$ false))

Boolean expressions are represented very similarly to algebraic expressions, the only difference being the specific values and operators used. Boolean expressions use true and false as constant values, and the operators include $\land$ (AND), $\lor$ (OR), $\neg$ (NOT).

References

^ ^a ^b ^c Bruno R. Preiss (1998). "Expression Trees". Archived from the original on January 19, 2017. Retrieved December 20, 2010.
^ Gopal, Arpita. Magnifying Data Structures. PHI Learning, 2010, p. 353.

This page was last edited on 24 February 2024, at 17:17

From Wikipedia, the free encyclopedia