
The tidal force or tide-generating force is a gravitational effect that stretches a body along the line towards and away from the center of mass of another body due to spatial variations in strength in gravitational field from the other body. It is responsible for the tides and related phenomena, including solid-earth tides, tidal locking, breaking apart of celestial bodies and formation of ring systems within the Roche limit, and in extreme cases, spaghettification of objects. It arises because the gravitational field exerted on one body by another is not constant across its parts: the nearer side is attracted more strongly than the farther side. The difference is positive in the near side and negative in the far side, which causes a body to get stretched. Thus, the tidal force is also known as the differential force, residual force, or secondary effect of the gravitational field.
In celestial mechanics, the expression tidal force can refer to a situation in which a body or material (for example, tidal water) is mainly under the gravitational influence of a second body (for example, the Earth), but is also perturbed by the gravitational effects of a third body (for example, the Moon). The perturbing force is sometimes in such cases called a tidal force[2] (for example, the perturbing force on the Moon): it is the difference between the force exerted by the third body on the second and the force exerted by the third body on the first.[3]
Tidal forces have also been shown to be fundamentally related to gravitational waves.[4]
YouTube Encyclopedic
-
1/5Views:1 707 17986 0001 009 7642 058 312433
-
Tides: Crash Course Astronomy #8
-
Visualization of Tidal Forces
-
How the tides REALLY work
-
What Physics Teachers Get Wrong About Tides! | Space Time | PBS Digital Studios
-
Geography Class-9 by Vilas sir / UPSC IAS GS Foundation 2025 (2pm to 4 pm)
Transcription
Y’know, if Shakespeare had been an astronomer, he’d have said that “there is a tide in the affairs of the Universe, and on such a full sea are we now afloat.” He would’ve been right. You might just think of tides as the ocean going in and out every day, but in fact what astronomers call tides are a subtle but inexorable force that have literally shaped most objects in the Universe. And to understand tides, we start with gravity. Gravity is a force, and it weakens with distance. An important thing to note is that we measure gravity from the center of mass of an object, not its surface. One way to think of the center of mass of an object is the average position in an object of all its mass. For an evenly distributed sphere, that’s it’s center. Right now, unless you’re an astronaut, you’re about 6400 kilometers from the center of the Earth. If you stand up, your head is a couple of meters farther away from the Earth’s center than your feet. Since gravity weakens with distance, the force of Earth’s gravity on your head is an eensy weensy bit less than it is on your feet. How much less? A mere 0.00005%. And that’s way too small for you to ever notice. But what if you were taller? Well, the taller you are, the farther your head is from the Earth’s center, and the weaker force it will feel. If you were, say, about 300 kilometers tall, the force of gravity would drop by about 10% at your head. That probably would be enough to notice, if you weren’t dying from asphyxiation and, y’know, being 300 kilometers tall. This change in the force of gravity over distance is what astronomers call the tidal force. When you have a massive object affecting another object with its gravity, its tidal force depends on several factors. For one thing, it depends on how strong the gravity is from the first object; the stronger the force of gravity, the stronger stronger the tidal force will be on the affected object. It also depends on how wide the affected object is. The wider it is, the more the force of gravity from the first object changes across it, and the bigger the tidal force. Finally, it depends on how far the affected object is from the first object. The farther away the affected object is, the lower the tidal force will be. Tides depend on gravity, and if gravity is weaker, so is the tidal force. The overall effect of the tidal force is to stretch an object. You’re applying a stronger force on one end than you are on the other, so you’re pulling harder on one end. That’ll stretch it! And this is where tidal forces become very important. Look at the Moon. It has gravity, but much less than the Earth because it’s less massive. It’s 380,000 kilometers away, so the gravitational force it has on you is pretty small. And you’re pretty small compared to that distance, just a couple of meters long from head to feet. But the Earth is big! It’s nearly 13,000 kilometers across. That means the side of the Earth facing the Moon is about 13,000 kilometers closer to the Moon than the other side of the Earth. This is a pretty big distance, enough for tides to become important. The side of the Earth facing the Moon is pulled harder by the Moon than the other side of the Earth, so the Earth stretches. It becomes ever so slightly football-shaped, like a sphere with two bulges, one pointing toward the Moon, and one pointing away. This is probably the weirdest thing about tidal forces. You might expect only one bulge, on the side of the Earth facing the Moon. But remember, we measure gravity from the centers of objects. The side of the Earth facing the Moon feels a stronger pull toward the Moon than the Earth’s center, so it’s pulled away from the center. But the side facing away from the Moon feels a weaker force toward the Moon than the Earth’s center. This means the center of the Earth is being pulled away from the far side. This is exactly the same as if the far side is being pulled away from the center, and that’s why you get two bulges on opposite sides of the Earth. The tidal force is therefore strongest on the sides of the Earth facing toward and away from the Moon, and weakest halfway in between them on each side. A lot of the Earth is covered in water, and water responds to this changing force, this stretching. The water bulges up where the tidal force is strongest, on opposite sides of the Earth. If there’s a beach on one of those spots, the water will cover it, and we say it’s high tide. If a beach is where the tidal force is low, the water’s been pulled away from it, and it’s low tide. But wait a second: The Earth is spinning! If you’re on the part of the Earth facing the Moon, you’re at high tide. Six hours later, a quarter of a day, the Earth’s rotation has swept you around to the spot where it’s low tide. Six hours after that you’re at high tide again, and then another six hours later you’re at low tide for the second time that day. Finally, a day after you started, you’re back at high tide once more. And that’s why we have two high tides and two low tides every day. Very generally speaking, the ocean tide causes the sea level to rise and fall by a meter or two, every day. Incidentally, the solid Earth can bulge as well. It’s not as fluid as water, but it can move. The tidal force stretches the solid Earth by about 30 centimeters. If you just sit in your house all day, you move up and down by about that much...twice! Like the saying goes, a rising tide lifts all… surfaces. The Earth’s spin has another effect. Lag in the water flow means the water can’t respond instantly to the tidal force from the Moon. The Earth’s spin actually sweeps the bulges forward a bit along the Earth. So picture this: the bulge nearest the Moon is actually a bit ahead of the Earth-Moon line. That bulge has mass; not a lot, but some. Since it has mass, it has gravity, and that pulls on the Moon. It pulls the Moon forward in its orbit a bit, like pulling on a dog’s leash, accelerating it. The Moon responds to this tug by going into a higher orbit: The Moon is actually moving away from the Earth! The rate of recession of the moon has been measured and it’s something like a few centimeters per year, roughly the same speed your fingernails grow. Now get this: the Moon has gravity. Just as the bulge is pulling the Moon ahead, the Moon is pulling the bulge back, slowing it down. Because of friction with the rest of the Earth, this slowing of the bulge is actually slowing the rotation of the Earth itself, making the day longer. The effect is small, but again it’s measurable. OK, let’s get a little change of perspective. Everything I’ve said about the Moon’s tidal effect on the Earth works the other way, too. The Moon feels tides from the Earth, and they’re pretty strong because the Earth is more massive and has more gravity than the Moon. Just like Earth, there are two tidal bulges on the Moon; one facing the Earth and one facing away. Long ago, the Moon was closer to the Earth, and spinning rapidly. The Moon’s tidal bulges didn’t align with the Earth, and the Earth’s gravity tugged on them, slowing the Moon’s spin and moving it farther away. As it moved farther away, the time it took to orbit once around the Earth increased: Its orbital period got longer. Eventually, the lengthening rotation of the Moon matched how long it took to go around the Earth. When that happened, the axis of the bulges pointed right at the Earth. That’s why the Moon only shows one face to us! It spins once per month, and goes around us once per month. If it didn’t spin at all, over that month we’d see the entire lunar surface. But since it does spin once per orbit, we only ever see one face. This is called tidal locking, and it’s worked on nearly every big moon in the solar system; tides from their home planet have matched their spin and orbital period. These moons all show the same face toward their planet! Now wait a second. If the Moon has gravity, which causes tides, and is the root cause behind all these shenanigans, what about the Sun? It’s even bigger than the Moon! Tides depends on the gravity from an object, and your distance from it. The Sun is far more massive than the Moon, but much farther away. These two effects largely cancel each other out, and when you do the math, you find the Sun’s tidal force on the Earth is just about half that of the Moon’s. The way the Sun’s tidal force and the Moon’s tidal force interact on Earth depends on their geometry, which changes as the Moon orbits us. At new Moon, the Earth, Moon, and Sun are in a line. The Moon’s tidal force aligns with the Sun’s, reinforcing it. This means we get an extra high high tide and an extra low low tide on Earth. We call this the spring tide. When the Moon is at first quarter, the tidal bulge from the Moon is 90° around from the Sun’s; high tide from the Moon overlaps low tide from the Sun. We get a slightly lower high tide, and a slightly higher low tide. We call those neap tides. The pattern repeats when the Moon is full; the Moon, Earth, and Sun fall along a line again, and we get spring tides. A week later the Moon has moved around, and we get neap tides again. Not only that, the Moon orbits the Earth on an ellipse. When it’s closest to us we feel a stronger effect. If that also happens at New or Full Moon, we get an added kick to the spring tides. This is called the proxigean tide, and can lead to flooding in low-lying areas. Unless you live on the coast, I bet you had no idea tides were so complex! Tides are universal; they work wherever there’s gravity. If two stars orbit each other, each raises a tide in the other. Just like the Earth and Moon, that can slow their spin and increase their separation. Many planets orbiting other stars may be tidally locked to those stars. Near a black hole, where the gravity is incredibly intense, the tides are so strong they would pull you like taffy into a long, thin string. Astronomers call this effect… spaghettification. No, seriously, that’s what we call it! Today you learned that tides are due to the changing force of gravity over distance. The strength of the tidal force from an object depends on the gravity of the object, and the size of and distance to the second object. Tides raise two bulges in an object, creating two high tides and two low tides per day on Earth. Tides have slowed the Earth’s rotation, moved the Moon away from the Earth, and locked the Moon’s rotation and orbit so that the Moon always has one side facing us. So. Tide goes in. Tide goes out. It turns out, I can explain that. Now you can too. Crash Course is produced in association with PBS Digital Studios. This episode was written by me, Phil Plait. The script was edited by Blake de Pastino, and our consultant is Dr. Michelle Thaller. It was co-directed by Nicholas Jenkins and Nicole Sweeney, and the graphics team is Thought Café.
Explanation
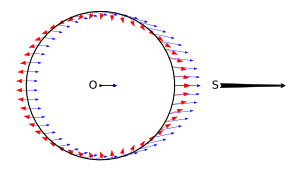
Earth's rotation accounts further for the occurrence of two high tides per day on the same location. In this figure, the Earth is the central black circle while the Moon is far off to the right. It shows both the tidal field (thick red arrows) and the gravity field (thin blue arrows) exerted on Earth's surface and center (label O) by the Moon (label S). The outward direction of the arrows on the right and left of the Earth indicates that where the Moon is at zenith or at nadir.
When a body (body 1) is acted on by the gravity of another body (body 2), the field can vary significantly on body 1 between the side of the body facing body 2 and the side facing away from body 2. Figure 2 shows the differential force of gravity on a spherical body (body 1) exerted by another body (body 2).
These tidal forces cause strains on both bodies and may distort them or even, in extreme cases, break one or the other apart.[5] The Roche limit is the distance from a planet at which tidal effects would cause an object to disintegrate because the differential force of gravity from the planet overcomes the attraction of the parts of the object for one another.[6] These strains would not occur if the gravitational field were uniform, because a uniform field only causes the entire body to accelerate together in the same direction and at the same rate.
Size and distance
The relationship of an astronomical body's size, to its distance from another body, strongly influences the magnitude of tidal force.[7] The tidal force acting on an astronomical body, such as the Earth, is directly proportional to the diameter of the Earth and inversely proportional to the cube of the distance from another body producing a gravitational attraction, such as the Moon or the Sun. Tidal action on bath tubs, swimming pools, lakes, and other small bodies of water is negligible.[8]
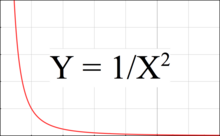
Figure 3 is a graph showing how gravitational force declines with distance. In this graph, the attractive force decreases in proportion to the square of the distance (Y = 1/X2), while the slope (Y′ = −2/X3) is inversely proportional to the cube of the distance.
The tidal force corresponds to the difference in Y between two points on the graph, with one point on the near side of the body, and the other point on the far side. The tidal force becomes larger, when the two points are either farther apart, or when they are more to the left on the graph, meaning closer to the attracting body.
For example, even though the Sun has a stronger overall gravitational pull on Earth, the Moon creates a larger tidal bulge because the Moon is closer. This difference is due to the way gravity weakens with distance: the Moon's closer proximity creates a steeper decline in its gravitational pull as you move across Earth (compared to the Sun's very gradual decline from its vast distance). This steeper gradient in the Moon's pull results in a larger difference in force between the near and far sides of Earth, which is what creates the bigger tidal bulge.
Gravitational attraction is inversely proportional to the square of the distance from the source. The attraction will be stronger on the side of a body facing the source, and weaker on the side away from the source. The tidal force is proportional to the difference.[8]
Sun, Earth, and Moon
The Earth is 81 times more massive than the Moon, the Earth has roughly 4 times the Moon's radius. As a result, at the same distance, the tidal force of the Earth at the surface of the Moon is about 20 times stronger than that of the Moon at the Earth's surface.[9]
| Gravitational body causing tidal force | Body subjected to tidal force | Tidal acceleration | |||
|---|---|---|---|---|---|
| Body | Mass () | Body | Radius () | Distance () | |
| Sun | 1.99×1030 kg | Earth | 6.37×106 m | 1.50×1011 m | 5.05×10−7 m⋅s−2 |
| Moon | 7.34×1022 kg | Earth | 6.37×106 m | 3.84×108 m | 1.10×10−6 m⋅s−2 |
| Earth | 5.97×1024 kg | Moon | 1.74×106 m | 3.84×108 m | 2.44×10−5 m⋅s−2 |
| G is the gravitational constant = 6.674×10−11 m3⋅kg−1⋅s−2[10] | |||||
Effects

In the case of an infinitesimally small elastic sphere, the effect of a tidal force is to distort the shape of the body without any change in volume. The sphere becomes an ellipsoid with two bulges, pointing towards and away from the other body. Larger objects distort into an ovoid, and are slightly compressed, which is what happens to the Earth's oceans under the action of the Moon. All parts of the Earth are subject to the Moon's gravitational forces, causing the water in the oceans to redistribute, forming bulges on the sides near the Moon and far from the Moon.[12]
When a body rotates while subject to tidal forces, internal friction results in the gradual dissipation of its rotational kinetic energy as heat. In the case for the Earth, and Earth's Moon, the loss of rotational kinetic energy results in a gain of about 2 milliseconds per century. If the body is close enough to its primary, this can result in a rotation which is tidally locked to the orbital motion, as in the case of the Earth's moon. Tidal heating produces dramatic volcanic effects on Jupiter's moon Io. Stresses caused by tidal forces also cause a regular monthly pattern of moonquakes on Earth's Moon.[7]
Tidal forces contribute to ocean currents, which moderate global temperatures by transporting heat energy toward the poles. It has been suggested that variations in tidal forces correlate with cool periods in the global temperature record at 6- to 10-year intervals,[13] and that harmonic beat variations in tidal forcing may contribute to millennial climate changes. No strong link to millennial climate changes has been found to date.[14]

Tidal effects become particularly pronounced near small bodies of high mass, such as neutron stars or black holes, where they are responsible for the "spaghettification" of infalling matter. Tidal forces create the oceanic tide of Earth's oceans, where the attracting bodies are the Moon and, to a lesser extent, the Sun. Tidal forces are also responsible for tidal locking, tidal acceleration, and tidal heating. Tides may also induce seismicity.
By generating conducting fluids within the interior of the Earth, tidal forces also affect the Earth's magnetic field.[15]
Formulation

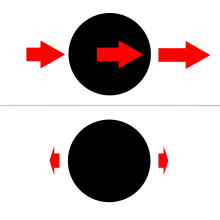
For a given (externally generated) gravitational field, the tidal acceleration at a point with respect to a body is obtained by vector subtraction of the gravitational acceleration at the center of the body (due to the given externally generated field) from the gravitational acceleration (due to the same field) at the given point. Correspondingly, the term tidal force is used to describe the forces due to tidal acceleration. Note that for these purposes the only gravitational field considered is the external one; the gravitational field of the body (as shown in the graphic) is not relevant. (In other words, the comparison is with the conditions at the given point as they would be if there were no externally generated field acting unequally at the given point and at the center of the reference body. The externally generated field is usually that produced by a perturbing third body, often the Sun or the Moon in the frequent example-cases of points on or above the Earth's surface in a geocentric reference frame.)
Tidal acceleration does not require rotation or orbiting bodies; for example, the body may be freefalling in a straight line under the influence of a gravitational field while still being influenced by (changing) tidal acceleration.
By Newton's law of universal gravitation and laws of motion, a body of mass m at distance R from the center of a sphere of mass M feels a force ,
equivalent to an acceleration ,
where is a unit vector pointing from the body M to the body m (here, acceleration from m towards M has negative sign).
Consider now the acceleration due to the sphere of mass M experienced by a particle in the vicinity of the body of mass m. With R as the distance from the center of M to the center of m, let ∆r be the (relatively small) distance of the particle from the center of the body of mass m. For simplicity, distances are first considered only in the direction pointing towards or away from the sphere of mass M. If the body of mass m is itself a sphere of radius ∆r, then the new particle considered may be located on its surface, at a distance (R ± ∆r) from the centre of the sphere of mass M, and ∆r may be taken as positive where the particle's distance from M is greater than R. Leaving aside whatever gravitational acceleration may be experienced by the particle towards m on account of m's own mass, we have the acceleration on the particle due to gravitational force towards M as:
Pulling out the R2 term from the denominator gives:
The Maclaurin series of is which gives a series expansion of:
The first term is the gravitational acceleration due to M at the center of the reference body , i.e., at the point where is zero. This term does not affect the observed acceleration of particles on the surface of m because with respect to M, m (and everything on its surface) is in free fall. When the force on the far particle is subtracted from the force on the near particle, this first term cancels, as do all other even-order terms. The remaining (residual) terms represent the difference mentioned above and are tidal force (acceleration) terms. When ∆r is small compared to R, the terms after the first residual term are very small and can be neglected, giving the approximate tidal acceleration for the distances ∆r considered, along the axis joining the centers of m and M:
When calculated in this way for the case where ∆r is a distance along the axis joining the centers of m and M, is directed outwards from to the center of m (where ∆r is zero).
Tidal accelerations can also be calculated away from the axis connecting the bodies m and M, requiring a vector calculation. In the plane perpendicular to that axis, the tidal acceleration is directed inwards (towards the center where ∆r is zero), and its magnitude is in linear approximation as in Figure 2.
The tidal accelerations at the surfaces of planets in the Solar System are generally very small. For example, the lunar tidal acceleration at the Earth's surface along the Moon–Earth axis is about 1.1×10−7 g, while the solar tidal acceleration at the Earth's surface along the Sun–Earth axis is about 0.52×10−7 g, where g is the gravitational acceleration at the Earth's surface. Hence the tide-raising force (acceleration) due to the Sun is about 45% of that due to the Moon.[17] The solar tidal acceleration at the Earth's surface was first given by Newton in the Principia.[18]
See also
- Amphidromic point
- Disrupted planet
- Galactic tide
- Tidal resonance
- Tidal stripping
- Tidal tensor
- Spacetime curvature
References
- ^ "Hubble Views a Cosmic Interaction". nasa.gov. NASA. February 11, 2022. Retrieved 2022-07-09.
- ^ "On the tidal force", I. N. Avsiuk, in "Soviet Astronomy Letters", vol. 3 (1977), pp. 96–99.
- ^ See p. 509 in "Astronomy: a physical perspective", M. L. Kutner (2003).
- ^ arXiv, Emerging Technology from the (2019-12-14). "Tidal forces carry the mathematical signature of gravitational waves". MIT Technology Review. Retrieved 2023-11-12.
- ^
R Penrose (1999). The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics. Oxford University Press. p. 264. ISBN 978-0-19-286198-6.
tidal force.
- ^ Thérèse Encrenaz; J -P Bibring; M Blanc (2003). The Solar System. Springer. p. 16. ISBN 978-3-540-00241-3.
- ^ a b "The Tidal Force | Neil deGrasse Tyson". www.haydenplanetarium.org. Retrieved 2016-10-10.
- ^ a b Sawicki, Mikolaj (1999). "Myths about gravity and tides". The Physics Teacher. 37 (7): 438–441. Bibcode:1999PhTea..37..438S. CiteSeerX 10.1.1.695.8981. doi:10.1119/1.880345. ISSN 0031-921X.
- ^ Schutz, Bernard (2003). Gravity from the Ground Up: An Introductory Guide to Gravity and General Relativity (illustrated ed.). Cambridge University Press. p. 45. ISBN 978-0-521-45506-0. Extract of page 45
- ^ "2022 CODATA Value: Newtonian constant of gravitation". The NIST Reference on Constants, Units, and Uncertainty. NIST. May 2024. Retrieved 2024-05-18.
- ^ R. S. MacKay; J. D. Meiss (1987). Hamiltonian Dynamical Systems: A Reprint Selection. CRC Press. p. 36. ISBN 978-0-85274-205-1.
- ^ Rollin A Harris (1920). The Encyclopedia Americana: A Library of Universal Knowledge. Vol. 26. Encyclopedia Americana Corp. pp. 611–617.
- ^ Keeling, C. D.; Whorf, T. P. (5 August 1997). "Possible forcing of global temperature by the oceanic tides". Proceedings of the National Academy of Sciences. 94 (16): 8321–8328. Bibcode:1997PNAS...94.8321K. doi:10.1073/pnas.94.16.8321. PMC 33744. PMID 11607740.
- ^ Munk, Walter; Dzieciuch, Matthew; Jayne, Steven (February 2002). "Millennial Climate Variability: Is There a Tidal Connection?". Journal of Climate. 15 (4): 370–385. Bibcode:2002JCli...15..370M. doi:10.1175/1520-0442(2002)015<0370:MCVITA>2.0.CO;2.
- ^ "Hungry for Power in Space". New Scientist. 123: 52. 23 September 1989. Retrieved 14 March 2016.
- ^ "Inseparable galactic twins". ESA/Hubble Picture of the Week. Retrieved 12 July 2013.
- ^ The Admiralty (1987). Admiralty manual of navigation. Vol. 1. The Stationery Office. p. 277. ISBN 978-0-11-772880-6., Chapter 11, p. 277
- ^ Newton, Isaac (1729). The mathematical principles of natural philosophy. Vol. 2. p. 307. ISBN 978-0-11-772880-6., Book 3, Proposition 36, Page 307 Newton put the force to depress the sea at places 90 degrees distant from the Sun at "1 to 38604600" (in terms of g), and wrote that the force to raise the sea along the Sun-Earth axis is "twice as great" (i.e., 2 to 38604600) which comes to about 0.52 × 10−7 g as expressed in the text.
External links
- Analysis and Prediction of Tides: GeoTide
- Gravitational Tides by J. Christopher Mihos of Case Western Reserve University
- Audio: Cain/Gay – Astronomy Cast Tidal Forces – July 2007.
- Gray, Meghan; Merrifield, Michael. "Tidal Forces". Sixty Symbols. Brady Haran for the University of Nottingham.
- Pau Amaro Seoane. "Stellar collisions: Tidal disruption of a star by a massive black hole". Retrieved 2018-12-28.
- Myths about Gravity and Tides by Mikolaj Sawicki of John A. Logan College and the University of Colorado.
- Tidal Misconceptions by Donald E. Simanek
- Tides and centrifugal force by Paolo Sirtoli





















